【程序设计】4.1 [排成队] 序列
4.1 序列
前面我们写过的程序中,输入的原始数据只有不多的几个。循环代码处理的多个数据,也是有某种规律被代码算出来的,不算是代码的原始数据了。实际工作中我们要处理的原始数据常常也是一大批,这时候就需要用到集合概念了。
不过,大多数程序设计语言并没有延用集合这个术语,而是用数组来表示成批的数据。SPL 则为了强调批量数据之间的次序,而用了序列这个术语。序列和数组可以理解成是同一种东西,只是习惯叫法不同,在本书中主要会使用序列这个词。
一批数据按次序可以构成一个序列,起一个变量名来存储和命名,这些构成序列的数据称为序列的成员,构成序列的成员个数称为序列的长度。
SPL 中,在方括号中把数据依次写出来,用逗号分隔,就可以得到序列常数,比如:
A |
|
1 |
[1,2,3,4,5] |
2 |
=[3,9,0,2,2.3,9.8] |
3 |
=[] |
A1 和 A2 都是序列,其中 A1 是常数格,A2 是计算格。A3 也是计算格,它的结果是个空序列,也就是没有成员的序列,空序列的长度为 0。不过,空序列并不是空值。
很多程序语言中,数组的成员必须是同一种数据类型。但在 SPL 中没有做这个要求,序列的成员可以有不同数据类型,不过大多数情况序列还是由相同数据类型成员构成。
序列成员还可以用使用其它变量或表达式:
A |
B |
C |
D |
|
1 |
3 |
=4+8 |
=pi() |
=3*C1 |
2 |
=[3,A1,D1,3*B1] |
=[B1,C1+A1,0] |
A2、B2 也可以定义出一个序列,但这种需要计算出来的序列必须使用计算格来定义,并且需要被执行后才有值。
SPL 中还可以像 Excel 一样用一片格子来定义一个序列:
A |
B |
C |
D |
|
1 |
4 |
8 |
3 |
2 |
2 |
5 |
2 |
0 |
-5 |
3 |
=[A1:D2] |
A3 中计算出一个长度为 8 的序列,成员按单元格的次序从左到右从上到下排列,这个序列即相当于 [4,8,3,2,5,2,0,-5]。
用在序列变量后用圆括号加序号,就可以访问序列中这个序号对应的成员,取值和赋值都可以:
A |
B |
C |
D |
|
1 |
4 |
8 |
3 |
2 |
2 |
5 |
9 |
0 |
-5 |
3 |
=[A1:D2] |
=A3(2) |
=A3(5) |
>A3(4)=3 |
4 |
=A3(1)+A3(3) |
=A3(A3(4)) |
=A3(A4) |
执行完后,B3 和 C3 的格值分别是 8 和 5。D3 格执行完后会使 A3 的第 4 个成员变成 3(之前是 2),但不会把改变 D1 的值,在 A3 赋值时已经把 D1 的值抄到 A3 的成员中了,再改 A3 的成员时和 D1 已经无关了。
序列成员可以参与运算,还可以作为序号来引用序列的其它成员。上面 A4 将计算出 7,B4 将计算出 8,C4 将计算出 0。
序列成员的序号,有时也称为其在序列中的位置。
点中序列所在格,开发环境也能显示出序列的取值,将列成表状,比如上面代码的 A3:
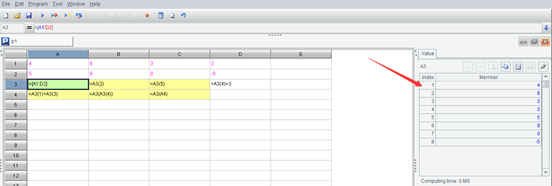
SPL 中序列的成员序号是从 1 开始的,引用成员使用圆括号。有些程序语言中数组的成员序号是从 0 开始的,引用成员是使用方括号。这也是学习程序语言的一个注意事项。
其实,序列变量可以被简单地理解成一批变量起了同一个名字,要用序号来区分,每个成员都可以看成是个独立的变量。如果序号超出界限,就相当于引用了一个不存在的变量,程序将报出错误。
上面说的生成序列的办法,要一个个把成员写出来(用单元格区域产生其实也是这样),如果我们要产生一个几百上千成员的序列,那这种办法显然就不靠谱了。
在 SPL 中,可以用表达式 [x]*n 的语法生成一个长度为 n、每个成员都是 x 的序列。比如 [0]*100 将返回一个由 100 个 0 作为成员的序列,这样我们可以造一个任意长度的序列。
这种办法造出的序列,其成员都会有个初始值。那么,能不能没有初始值,只要一个留有空位的序列?
其实这是没有意义的,计算机程序中的任何一个变量,总会占一点存储空间,而这个存储空间里也总会有点数据,所不同的只是根据这个变量类型来如何解释这些数据了,不存在不占存储空间的“真空”值。我们平时说的空值,即 null,也是一种数据类型,它也要占点存储空间。也可以用 [null]*n 来产生序列,不过和 [0]*n 在空间占用上并没有多大区别。
在 SPL 中, null 和 0 是不一样的,即 null!=0 将计算出 true,类似的语言还有 SQL;但有些程序语言中 null 和 0 是一回事(比如 C 语言)。
我们后面再讲如何产生和处理一个长度不确定的序列。
有了序列后,我们可以把前面计算水仙花数的例子改一下,把所有的水仙花数计算出来写到一个序列中:
A |
B |
C |
D |
E |
F |
|
1 |
=0 |
=[0]*100 |
||||
2 |
for 9 |
=100*A2 |
=A2*A2*A2 |
|||
3 |
for 0,9 |
=B2+10*B3 |
=C2+B3*B3*B3 |
if C3<D3 |
break |
|
4 |
for 0,9 |
=C3+C4 |
=D3+C4*C4*C4 |
|||
5 |
if D4==E4 |
>A1+=1 |
>B1(A1)=D4 |
|||
6 |
else if D4<E4 |
break |
假定最多 100 个水仙花数(其实远少于 100),在 B1 生成一个长度为 100 的序列,A1 是当前找到的水仙花数的个数,每找到一个,让 A1 增加 1,再把 B1 的相应成员填上。最后 B1 前面那些不是 0 的成员就是所有的水仙花数了。
分解质因数的问题,我们后面再改造。
我们再来用序列实现一个经典的算法,冒泡排序。
给一组数,或者就说是一个序列,我们要把这个序列的成员从小到大重新排列出来。
冒泡排序的算法过程是这样:从前向后扫描这个序列,如果发现相邻成员的大小不合适,比如前面的数比后面的数大了,则交换这两个数。扫描过一遍后,如果发生过交换动作,则要重新再扫描,直到某次扫描没有发生过交换,排序就完成了。
A |
B |
C |
D |
|
1 |
=[3,4,12,4,6,9,3,5] |
=A1.len()-1 |
=true |
|
2 |
for D1 |
>D1=false |
||
3 |
for C1 |
if A1(B3)>A1(B3+1) |
=A1(B3) |
|
4 |
>A1(B3)=A1(B3+1) |
|||
5 |
>A1(B3+1)=D3 |
|||
6 |
>D1=true |
|||
待排序数据在 A1 中。外层循环开始后,先把 D1 设为 false 以假定这是最后一次循环,然后扫描序列,发生过相邻成员大小不合适时则实施交换,然后把 D1 置为 true,这样可以进行下一轮外层循环。如果没有发生过交换,则 D1 保持为 false,外层循环结束。
冒泡排序还有一个常见的变种:
A |
B |
C |
D |
|
1 |
=[3,4,12,4,6,9,3,5] |
=A1.len() |
=C1-1 |
|
2 |
for D1 |
for A2+1,C1 |
if A1(A2)>A1(B2) |
=A1(A2) |
3 |
>A1(A2)=A1(B2) |
|||
4 |
>A1(B2)=D2 |
|||
请读者自己看懂其中的原理。
有了序列及其排序能力后,我们可以把前面那个黑洞数的问题简化一下,使用冒泡这个变种方案来排序(这里要从大到小排):
A |
B |
C |
D |
E |
|
1 |
1234 |
||||
2 |
for |
=[A1\1000,A1\100%10,A1\10%10,A1%10] |
>C6=D6=0 |
||
3 |
for 3 |
for B3+1,4 |
if B2(B3)<B2(C3) |
=B2(B3) |
|
4 |
>B2(B3)=B2(C3) |
||||
5 |
>B2(C3)=E3 |
||||
6 |
for 4 |
=C6*10+B2(B6) |
=D6*10+B2(5-B6) |
||
7 |
>output(A1) |
=C6-D6 |
if C7==A1 |
break |
|
8 |
>A1=C7 |
||||
因为有了序列,在计算四位数的时候也可以使用循环了(B6:D6),之前要把 C6 和 D6 都填成 0(E2 格),然后 B6:D6 的循环中就可以正确计算出最大最小这两个四位数了。E2 格中利用前面说过的 a=x 也被当成计算表达式而会有个值,D6=0 在把 D6 赋值为 0 的同时也会计算出 0,然后再赋值给 C6,结果 C6 和 D6 都变成 0 了。



