"量化交易是通过编程建模等方式，利用概率论、统计学等知识从庞大的历史数据中总结规律并建模量化模型，然后凭借计算机强大的计算能力来高效、快速地进行交易决策。编程语言可选择的语言很多，下图是来自于T .."

jiangzhucao 北京
乾学院 1061 号会员
2 回帖 • 651 浏览 • 1 年前

做量化模型用什么，试试 SPL？

计算＆AI

量化交易是通过编程建模等方式，利用概率论、统计学等知识从庞大的历史数据中总结规律并建模量化模型，然后凭借计算机强大的计算能力来高效、快速地进行交易决策。编程语言可选择的语言很多，下图是来自于TIOBE统计的从2002年至今前十位编程语言的走势图，可以看出，之前很长一段时间内Java和C语言一直占据着统治地位，但从2018年起伴随着人工智能的兴起，Python的地位迅速上升，现在已经超过了Java和C。

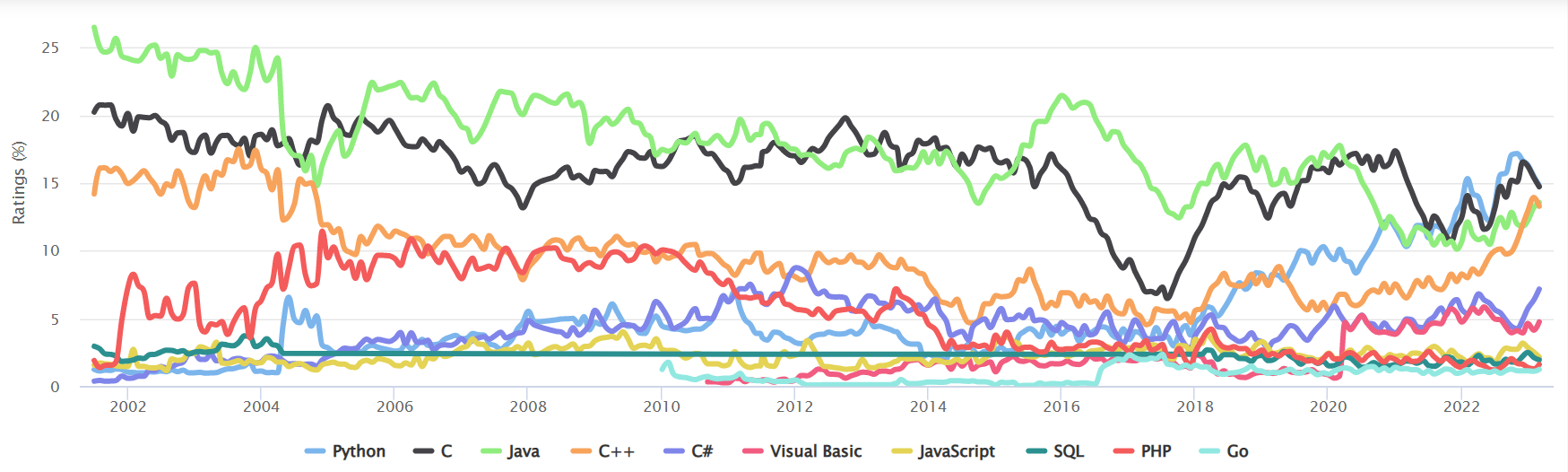
在量化领域也是类似，之前主流的语言有Java,C,C++,R,Matlab等，而现在基本都在用Python。的确相对于Java和C等语言，Python编程简单，数学和统计类函数丰富，使用起来很方便。

不过，对于开发量化模型来说，使用SPL经常会更方便。比如交互式编程体验，强大的数据准备功能，灵活的结构化数据操作等。虽然SPL的数学函数没有Python丰富，但是量化分析中很少用到非常高深的数学函数和巨大的AI模型，常用的算法也就是一些线性模型，数据平滑，PCA，统计检验等等，SPL中都有。在机器学习方面也可以使用SPL封装Python的功能实现自动化建模，使用起来比直接用Python还要方便。

话不多说，我们举个例子来体验一下。

1.经典策略：双移动平均策略的实现及回测

双移动平均策略是使用两条均线来判断股价未来的走势。在两条均线中，一条是长期均线（如10日均线），另一条是短期均线（如5日均线）。这种策略基于这样一种假设：股票价格的动量会朝着短期均线的方向移动。当短期均线穿过长期均线，超过长期移动平均线时，动量将向上，此时股票价格可能会上涨。然而，如果短期均线的移动方向相反，则股价可能下跌。

根据这个原理，我们来创建一个双移动平均交易策略。在这里我们使用代码为“002805”的股票数据为例来进行实验，回测期选取2021年一年的数据。初始资金设为50000元，交易费率设为0.0003。

操作步骤分为两部分，策略编写和回测，回测指标计算一年的收益。具体步骤如下：

策略编写：

（1）导入数据，按日期升序排序，并筛选出2021年的数据

（2）计算5日MA和10日MA添加到数据中

（3）设置一个交易信号signal，当5日均价大于10日均价时，标记为1，反之标记为0

（4）根据交易信号signal的变化下单，当交易信号从0变成1时买入，从1变为0时卖出，每次交易量都为1000股。用order字段来记录每次的下单数据。

回测：

（1）用stock字段来表示股票的持仓情况，stock等于所有交易量order的总和

（2）用stock_value来表示股票市值，股票市值等于持仓数量stock*股价

（3）用acctrade_cash来表示累计交易金额，交易金额包括下单金额和交易手续费

（4）用avaliable_cash表示可用现金，初始资金-累计交易金额就是可用现金

（5）用total来表示总资产，总资产=可用现金+股票市值，总资产的变化就是一年的收益情况。

分别用Python和SPL来实现代码如下。

Python代码：

import pandas as pd
import numpy as np
pd.set_option("display.max_rows",None)
pd.set_option("display.max_columns",None)

initial_cash=50000
fee=0.0003

#双移动平均策略
data = pd.read_csv("D://002805.csv", encoding='gbk')

data["Date"]=pd.to_datetime(data["Date"])

data = data.sort_values("Date")

data = data.loc[(data["Date"]>"2021/01/01")& (data["Date"]<"2022/01/01")]

data["MA_5"]=data["Close"].rolling(5).mean()
data["MA_10"]=data["Close"].rolling(10).mean()
data["signal"]=np.where(data["MA_5"]>data["MA_10"],1,0)
data["order"]=data["signal"].diff()*1000

#回测
position = pd.DataFrame(index=data.index).fillna(0)
position["Date"]=data["Date"]
position["stock"]=data["order"].cumsum()
position["stock_value"]=position["stock"]*data["Close"]
position["acctrade_cash"]=(data["order"]*data["Close"]*(1+fee)).cumsum()
position["avaliable_cash"]=initial_cash-position["acctrade_cash"]
position["total"]=position["avaliable_cash"]+position["stock_value"]
#投资收益
returns=(position["total"].iloc[-1]-initial_cash)*100/initial_cash
print(returns)

SPL代码：

	A
1	>initial_cash=50000
2	>fee=0.0003
3	=T("D://002805.csv").sort(Date).select(Date>date("2021/01/01") && Date<date("2022/01/01") )
4	=A3.derive(Close [-4:0]:Close_5,avg(Close [-4:0]):MA_5,avg(Close [-9:0]):MA_10,if(MA_5>MA_10,1,0):signal,(signal-signal[-1])*1000:order)	策略
5	=A4.new(stock[-1]+order:stock,stockClose:stock_value,acctrade_cash[-1]+orderClose*(1+fee):acctrade_cash)	回测
6	=A5.derive(initial_cash-acctrade_cash:avaliable_cash,avaliable_cash+stock_value:total)

对比两种代码，主要区别有以下几点。

（1）从直观的代码量来看，Python需要20多行，而SPL几行就可以搞定。

（2）量化编程的实验性特别强，很多时候都需要实时查看运行结果，虽然Python有很多IDE如Pycharm、Eclipse、Jupyter Notebook等等，但是最常用调试方法基本还是用print()把想看的值打印出来。例如我们要看筛选出2021年并按日期排序后的数据是否正确，需要在对应的Python语句后使用print()函数。

返回结果：

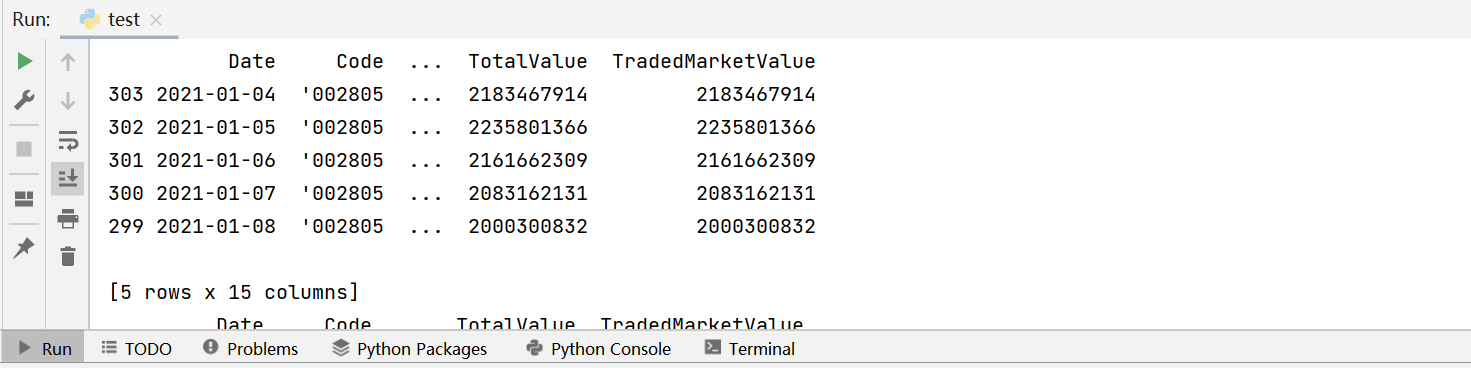
而SPL采用的是交互式编程方式，每一句代码的运行结果可以直接在界面生成，无需单独打印。并且数据的显示方式就像是在看excel表，用户体验非常友好。

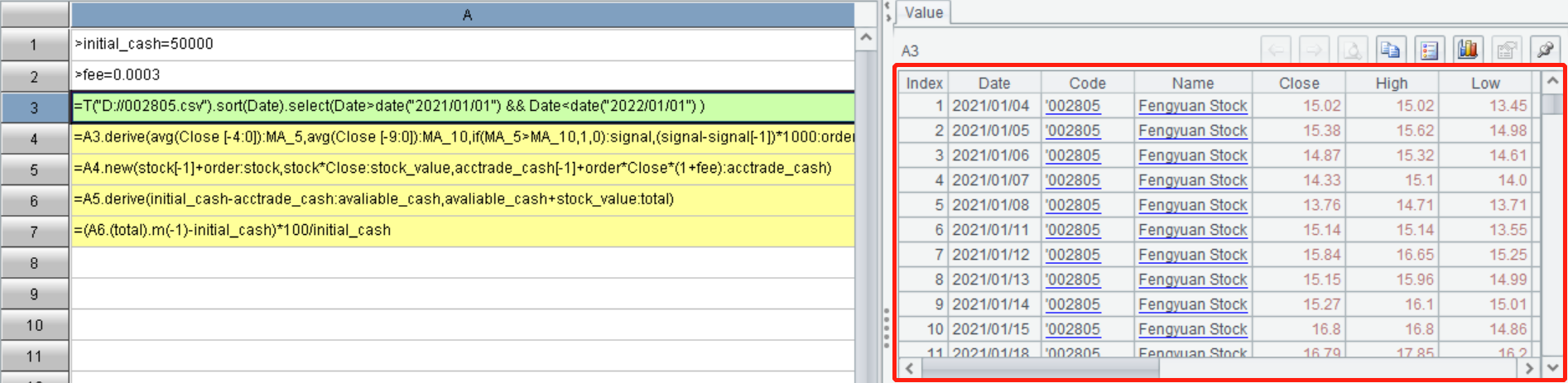
（3）Python 在添加字段时，需要一个一个的添加，并且反复引用表格。SPL可以直接在原表结构上衍生或新建多个字段，只需引用一次表格，代码更简单，效率也更高。

（4）SPL可以直接引用相邻记录进行计算，代码写起来更直观。而Python无法实现对相邻记录的直接引用，因此需要借助其他函数来实现。比如例子中移动平均值的计算。

Python移动平均:

data["MA_5"]=data["Close"].rolling(5).mean()
data["MA_10"]=data["Close"].rolling(10).mean()

SPL移动平均:

A3.derive(Close [-4:0]:Close_5,avg(Close [-4:0]):MA_5,avg(Close [-9:0]):MA_10)

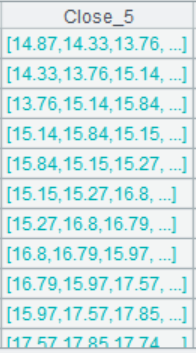
在SPL采用的是Close[-4:0]这种形式，引用邻近5日的收盘价格，然后求均值。Python则是用了一个rolling()函数，然后求均值。看起来似乎只是方法不同，代码都很简洁。但我们去查pandas的rolling()文档，发现其返回的并不是5日的收盘价而是一个子对象，和groupby()类似，通常要和mean(),sum()这样的函数一起使用。在一般的数据分析场景中简单的平均，汇总也就够了，但是在量化计算中，远远不够。比如我们想让这个5日移动价格指标反应更灵敏一些，按照5：4：3：2：1这样权重来加权平均。这时再查函数文档，它会告诉你默认所有窗口的值权重都是一样的，也有其他的权重方式，想了解更多，去查scipy的相关文档。到这里Python的实现方式就已经开始复杂起来，学习难度也陡然增加。

而在SPL里修改就简单多了,因为“Close[-4:0]”返回的就是5日的价格如下图，可以直接对其引用计算。代码如下表。

	A
1	=[5,4,3,2,1]
2	=A1.sum()
3	=T("D://002805.csv").sort(Date).select(Date>date("2021-01-01") && Date<date("2022-01-01") )
4	=A3.derive(Close[-4:0].sum(~*A1(#)/A2):WMA)

“~”和“#”表示在循环函数中取当前值和序号。

2.RSI指标计算

再来看一个稍微复杂一点的指标计算例子，RSI。

RSI相对强弱指标又叫力度指标，由威尔斯•魏尔德﹝Welles Wilder﹞所创造的，是目前股市技术分析中比较常用的中短线指标。

RSI是根据一定时期内股价上涨总幅度占股价变化总幅度的百分比制作出的一种技术曲线。代表股票在过去N天的相对强弱情况，能够反映出市场在一定时期内的景气程度。

RSI值域在0到100之间，值越大，股票表现越强势。 RSI大多数时间在30到70之间震荡。RSI > 80，代表超买，股价回调的可能性加大; RSI<20, 代表超卖，股价反弹的可能性增大。

计算方法：

RSI=（N日内上涨幅度的sma/N日内上涨和下跌幅度的sma）*100%

sma表示指数平均

sma=1日涨幅/N+(1-1/N)*昨日sma

1日涨幅=收盘价-昨日收盘价

上涨幅度取N日内1日涨幅中的正值

上涨和下跌幅度取N日内1日涨幅的绝对值

分别用Python和SPL来实现：

“Change”字段表示1日涨幅

“sma_up_change”字段表示上涨幅度sma

“sma_abs_change”字段表示上涨和下跌幅度的sma

Python代码：

import datetime

import pandas as pd

import numpy as np

pd.set_option("display.max_rows",None)

pd.set_option("display.max_columns",None)

n = 14

data=pd.read_csv("D://002805.csv", encoding='gbk')

data["Date"]=pd.to_datetime(data["Date"])

data=data.sort_values("Date")

data=data.loc[(data["Date"]>"2021/01/01")& (data["Date"]<"2022/01/01")]

data["Change"]= data["Close"]-data["Close"].shift(1)

data["Change"].iloc[0]=data["Close"].iloc[0]

length=len(data)

sma_up_change =[0]*length

sma_abs_change = [0]*length

rsi = [0]*length

sma_up_change[0]=data["Change"].iloc[0]/n

sma_abs_change[0]=sma_up_change[0]

for i in range(1,length):

sma_up_change[i]=max(data["Change"].iloc[i],0)/n+(1-1/n)*sma_up_change[i-1]

sma_abs_change[i]=abs(data["Change"].iloc[i])/n+(1-1/n)*sma_abs_change[i-1]

rsi[i]=sma_up_change[i]/sma_abs_change[i]*100

data["rsi"]=pd.Series(rsi,index=data.index)

SPL代码：

	A
1	14
2	=T("D://002805.csv").sort(Date).select(Date>date("2021/01/01") && Date<date("2022/01/01") )
3	=A2.new(Date,Close-Close[-1]:Change)
4	=A3.derive(max(Change,0)/A1+(1-1/A1)sma_up_change[-1]:sma_up_change,abs(Change)/A1+(1-1/A1)sma_abs_change[-1]:sma_abs_change)
5	=A4.new(Date,sma_up_change/sma_abs_change*100:RSI)

同样Python需要20多行完成的代码，SPL几行就完成了。

在实现方式上主要有两处区别。

（1）在计算1日涨幅=收盘价-昨日收盘价时，对昨日收盘价的取值方式不同

Python：

data["Close"].shift(1)

SPL:

Close[-1]

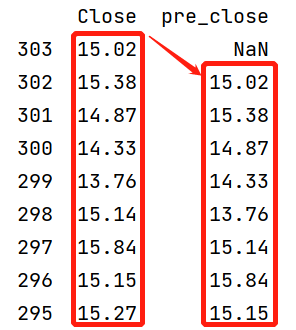
Python用的是偏移矩阵索引的方法，将收盘价整体向下移动一行来实现的，如下图。在这里也可以体现出dataframe其实就是一个数据“框”的概念，它不能对行相邻行记录直接引用，只能间接的绕道其他方式来解决。并且和上个例子中取相邻多行用的还是完全不同的方法。也就是说你会取一行，不一定会取很多行，会取很多行也不一会用不同的方法去取（比如MA,WMA）。在学习方法上Python并不是触类旁通，举一反三的。所以Python虽然看似入门容易但是真正掌握并不容易，有一种越学越多的感觉。

SPL在这方面优势就比较明显了，可以使用[-1],[-4:0]这种方式直接取到相邻的记录，公式的写法上和通信达等软件类似，符合自然的逻辑思维，容易理解。学习上只要掌握了基本语法，就可以举一反三，不需要记太多的函数。

（2）在计算sma时，Python无法直接在dataframe里进行循环计算，需要取出来用for循环计算后再放回去。而SPL由于可以直接引用每一行记录，因此在序表中就可进行递归计算。代码写起来很流畅，一点也不烧脑。

在量化计算中，对相邻行记录的引用非常频繁，用Python的话就比较麻烦。

Python: