6.4 质量守恒约束下的线性拟合
有边界的线性拟合方法保证拟合时收率被限制在边界内,误差限制法保证收率不偏离基础收率太远,现在只有约束2(所有出料对某一种进料的收率和等于1)还没有满足,本节将介绍一种线性变换的方法来满足此约束,从而求得最终的收率W。
利用进料矩阵X和基础收率B求得基础出料矩阵,用YB表示。
YB=X*B
对比Y与YB的差距,得到两者的偏差矩阵,用E表示。
E=Y-YB
用误差限制法计算偏差收率边界BD
BD=bd(X,Y,B,rg)
其中bd(…)是误差限制法,rg是边界调节比例rg∈[0,1]。
用有边界的线性拟合算法拟合X与E,得到偏差收率,用WE表示。
WE=BDfit(X,E,BD)
其中BDfit(…)是有边界线性拟合算法。
WE不能保证W满足约束2,但可以经过线性变换,在损失准确性最小的情况下得到满足约束条件的最佳偏差收率WD。
WD=L(WE)
其中L(…)是某种线性变换。
我们期望WD与基础收率B相加得到收率W,对W约束就转换为对WD的约束,如下图:
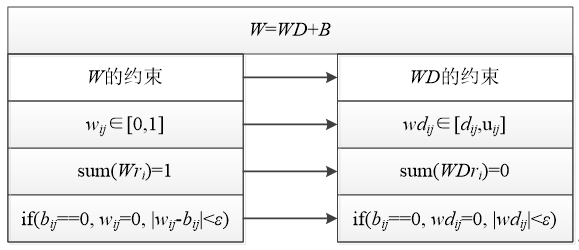
dij和uij分别是上界和下界。
理想情况下,WE各行的总和WRL是0,即WE的每一列与其他列的加和是线性关系。
利用这一线性关系可以对WE进行线性变换得到满足约束2的WD。
假设WE矩阵如下:
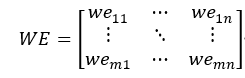
(1) 计算WE的各行总和WRL:
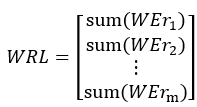
(2) 计算WE第j列以外的其他向量的总和组成的矩阵WS
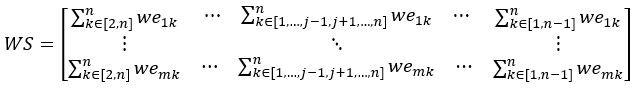
(3) 线性变换得到WD
WEcj,WScj,WRL三者有如下关系:
WEcj+WScj=WRL
WEcj是有边界线性拟合算法得到的第j列最佳收率,则WScj=WRL-WEcj也是准确的,进行如下线性变换得到WD’:
WD’cj=WEcj*(n-1)/n+ WScj*(-1/n)
=WEcj*(n-1)/n+(WEcj-WRL)/n
= WEcj-WRL/n
其中WD’cj是线性变换后的矩阵WD’的第j列元素。
线性变换后,相当于某个偏差收率weij减去其所在行的收率均值WRLi。
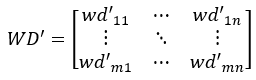
wd’ij=weij-WRLi/n
WD’满足约束2,但仍需验证WD’能否使W满足约束1,即wij=wd’ij+bij∈[0,1]。
如果W满足约束1,则拟合结束。
WD=WD’
如果存在wd’ij使得wij∉[0,1]时,需要调整变换规则。
假设WE中有z列存在不满足约束的元素。
WE=[WEc1,WEc2,…,WEc(1),…,WEc(z),…,WEcn]
其中[WEc(1),…,WEc(z)]是存在转换后仍不符合约束条件偏差收率列,即存在:
wei(p)+ bi(p)∉[0,1],p∈[1,z]
刚才的线性变换是WD’cj=WEcj*(n-1)/n+WScj*(-1/n),两者的变换系数是确定的,分别是(n-1)/n和(-1/n),但因为无法满足约束,所以不能用,可以换一个思路,把WEcj的变换系数固定为1,WScj的系数用解方程的方式求出来。
设WScj的系数向量是向量A,方程如下:
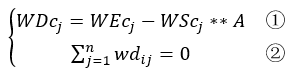
其中WDcj是偏差系数矩阵WD的第j列元素。
方程①②即可求得系数向量A,还要考虑基础收率bij等于0时,对应的收率weij也要等于0。
解方程得到向量A:
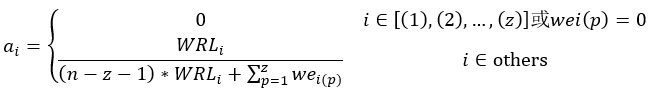
有了向量A后,带入方程①中,求得WDcj。
此时还要再验证一遍WD是否能使W满足约束1,如果满足,则计算结束,求得WD。否则还要把不满足约束条件的那一列加入到[WEc(1),…,WEc(z)],重复上述方法,直到所有wij都满足约束1(wij=(wdij+bij)∈[0,1]),得到WD。
最后用WD加基础收率矩阵B得到W。
W=B+WD
SPL例程
A |
B |
C |
D |
|
1 |
[[30,8],[31,7],[38,10]] |
/X |
||
2 |
[[2,13,23],[3,15,20],[11,13,24]] |
/Y |
||
3 |
[[0,0.5,0.5],[0.55,0.05,0.4]] |
/B |
||
4 |
0.1 |
/rg |
||
5 |
=mul(A1,A3) |
/X*B |
||
6 |
=A2.(~--A5(#)) |
/E |
||
7 |
=bd(A1,A2,A3,A4).(~.(~.(round(~,3)))) |
/BD |
||
8 |
=A6.~.((idx=#,bdfit(A1,A6.([~(idx)]),A7.(~(idx))).conj())) |
/WET |
||
9 |
=transpose(A8) |
/WE |
||
10 |
=func(A12,A9,A3) |
/WD |
||
11 |
/线性变换,参数:WE,B |
|||
12 |
func |
|||
13 |
=A12.(~.count(~==0)) |
/WE每行0的个数 |
||
14 |
=A12.~.len() |
/出料数 |
||
15 |
=A12.((s=~.sum(),ind=#,~.(if(~==0,0,s/(B14-B13(ind)))))) |
/各行求均值 |
||
16 |
=A12.(~--B15(#)) |
/weij-WRLi/n |
||
17 |
=B12.(~++B16(#)) |
/W=WD'+B |
||
18 |
=transpose(B17) |
|||
19 |
=B18.pselect@a(~.pselect(~<0||~>1)>0) |
/记录WD‘不满足约束的列索引 |
||
20 |
if B19.len()==0 |
return B17 |
/没有超限返回W |
|
21 |
else |
=func(A24,A12,B12,B19) |
/超限时变换规则 |
|
22 |
return C21 |
|||
23 |
/递归消除不符合约束2的元素 |
|||
24 |
func |
|||
25 |
=B24.~.len() |
|||
26 |
=A24.(~.sum()) |
/WRL |
||
27 |
=A24.((w=~,w.((ind=#,if(~==0,0,w(to(B25).delete(ind)).sum()))))) |
/WS |
||
28 |
=A24.(~.pselect@a(~==0)) |
/WEri中收率为0的索引 |
||
29 |
=B28.(~&C24) |
/不满足约束及等于0的索引 |
||
30 |
=B26.(~/((B25-B29(#).len()-1)*~+A24(#)(B29(#)).sum())) |
/ai |
||
31 |
=A24.((ind=#,~.(if(B29(ind).pos(#)>0,0,B30(ind))))) |
/A |
||
32 |
=B27.(~**B31(#)) |
/A**WScj |
||
33 |
=A24.((idx=#,if(B31(#).id()==[0],B32(#),~--B32(#)))) |
/WD |
||
34 |
=B24.(~++B33(#)) |
/B+WD |
||
35 |
=transpose(B34) |
/WT |
||
36 |
=B35.pselect@a(~.pselect(~<0||~>1)>0) |
/再次确认是否有超限收率 |
||
37 |
if B36.len()==0 |
return B34 |
/没有超限返回W |
|
38 |
else |
=C24=C24&B36 |
/有超限记录下来 |
|
39 |
=func(A24,A24,B12,C24) |
/WD |
||
A7格中的bd(…)是误差限制法,用来计算偏差收率边界BD;
A8格中的bdfit(…)是有边界的线性拟合算法。
A12格代码块对WE做线性变换;
A24格代码块对WD’做变换;
计算结果示例:
进料X:
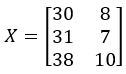
出料Y:

基础收率B:
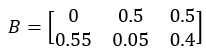
边界调节比例rg:
rg=0.1
算出的边界BD:
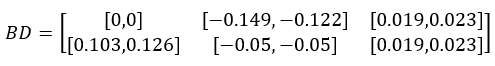
最终的收率W:
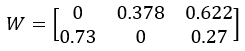
先来看使用基础收率B,各出料的MSE:
MSE1=12.24
MSE2=16.24
MSE3=8.98
其中MSEj是第j个出料的MSE。
再看使用W,各出料的MSE:
MSE1=10.97
MSE2=5.13
MSE3=3.86
很明显是拟合后的W效果更好。



