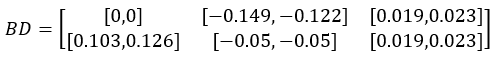6.3 误差限制法计算边界
为了满足约束3(收率不能偏离基础收率太远),将收率与基础收率的差称为偏差收率,记为WE。
WE=W-B
收率W范围是[0,1],基础收率B是固定的,偏差收率WE的理论最大范围是[-1,1],但这个范围太大了,实际生产中,进料和出料每天都会调整,计算收率时希望今天的收率尽可能和昨天一样,计算偏差收率边界范围时,可以把最后一天(行)的进料到出料转化率看作基准,利用这一基准和基础收率就能算出偏差收率边界BD,我们将此方法称为误差限制法。计算过程如下:
假设偏差收率边界BD形式如下:
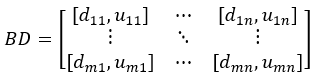
其中dij是第i个进料第j个出料的偏差收率下界,uij是第i个进料第j个出料的偏差收率上界。
进料和出料最后一行数据:
Xrm=[xm1,xm2,…,xmn]
Yrm=[ym1,ym2,…,ymn]
(1) 计算理论出料YTrm
YTrm=Xrm*B
(2) 理论出料与实际出料之差DFrm
DFrm= Yrm-YTrm
(3) 计算DFrm占总进料的比例Prm
Prm=DFrm/sum(Xrm)
(4) 计算偏差收率边界BD
设置一个BD允许调整的比例,记为pg。
BD的参考调整值d’mj和u’mj可根据Prm和pg来算,即:
d’mj=if(pmj>0,pmj*(1-pg), pmj*(1+pg))
u’mj=if(pmj>0,(pmj*(1+pg), pmj*(1-pg))
其中pmj是Prm的第j个元素。
本来所有进料相应的偏差收率都用这个边界就可以了,但是需要保证所有收率在[0,1]范围内,还要使基础收率为0时,收率也是0,边界上下限也必须是0。
dij和mij需要满足以下4个不等式:
dij+bij≥0
uij+bij≥0
dij+bij≤1
uij+bij≤1
根据不等式和基础收率B计算BD
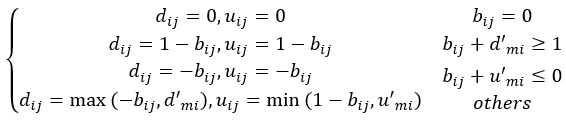
SPL例程
A |
B |
|
1 |
[[30,8],[31,7],[38,10]] |
/X |
2 |
[[2,13,23],[3,15,20],[11,13,24]] |
/Y |
3 |
[[0,0.5,0.5],[0.55,0.05,0.4]] |
/B |
4 |
0.1 |
/rg |
5 |
=A1.m(-1).sum() |
/Xrm总量 |
6 |
=mul([A1.m(-1)],A3).~ |
/理论出料量YTrm |
7 |
=A2.m(-1)--A6 |
/理论出料与实际出料差DFrm |
8 |
=A7.(~/A5) |
/DFrm占Xrm总量之比Prm |
9 |
=A8.([if(~>0,~*(1-A4),~*(1+A4)),if(~>0,~*(1+A4),~*(1-A4))]) |
/D'rm,U'rm |
10 |
=A3.(~.((r=A9(#),(if(~==0,[0,0],if(~+r(1)>1,[1-~,1-~],if(~+r(2)<0,[-~,-~],[max(-~,r(1)),min(1-~,r(2))]))))))) |
/偏差收率边界BD |
计算结果示例:
进料X:
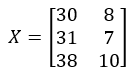
出料Y:
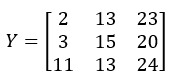
基础收率B:
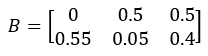
边界调节比例rg:
rg=0.1
算出的边界BD: