在积累了一些进料和出料的样本数据后，我们希望计算出收率矩阵。

如果没有任何约束条件，用最小二乘法就可以得到收率W。

W=linefit(X,Y)

其中linefit(…)是最小二乘线性拟合函数。

这时的W没有任何限制，其中的元素可能大于1或小于0，这对于生产就没有意义了，所以当考虑约束1时，简单的用最小二乘法来做就行不通了。

如果只考虑第一个约束条件，0和1是w_ij的边界，在这个边界范围内使得误差平方和MSE最小，即：

MSE=(Y-XW)²

w_ij∈[0,1]

可以证明，最优解要么出现在边界上，要么出现在最小二乘法拟合的值上，也就是说w_ij有三种可能的取值，分别是：

w_ij=0

w_ij=1

w_ij=linefit(…)，且满足w_ij∈[0,1]

当进料数有限时，穷举每种进料收率的3种可能就能拟合出最优解，m种进料就有3^m种可能，找到使MSE最小的一套收率即为边界范围内的最优解。我们把这种边界约束条件下求最优解的方法称为有边界的线性拟合算法。

以第一列出料Yc₁为例介绍有边界的线性拟合算法，其他进料是一样的。

1. 穷举进料收率所有可能的取值情况

每种进料的收率有3种可能取值，m种进料就相当于m重循环，所以可能的收率组合共有3^m种，记为s。

s=3^m

比如所有进料收率都取最小二乘拟合值时：

W(t) =linefit(X,Yc₁)

其中W(t)是Yc₁第t个收率矩阵，t∈[1,s]。

当所有进料收率都取下边界时：

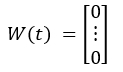
此时的收率矩阵就是m个0组成的m*1矩阵，其他取到边界的情况是一样的，边界本身就是该进料的收率。

当只有部分进料收率取到边界时：

其他进料的收率需要最小二乘法来求，假设进料Xc_a,Xc_b,…,Xc_l的收率取到了边界，这些进料的收率就是边界，为Wr_a,Wr_b,…,Wr_l。

收率没取到边界的进料记为X’，对应的出料需要减去边界收率与进料的乘积，记为Yc₁’

Yc₁’= Yc₁-(Xc_a*Wr_a+Xc_b* Wr_b+…+Xc_l*Wr_l)

X’的收率矩阵用最小二乘法来拟合，记为W(t)’

W(t)’=linefit(X’,Yc₁’)

W(t)’与W_aj,W_bj,…,W_kj共同构成第t个收率矩阵W(t)。

穷举完全部情况，共得到s个收率矩阵，从这s个收率矩阵中找出满足边界约束（即w_ij∈[0,1]）且MSE最小的收率就是最优收率。

2. 筛选满足边界条件的收率矩阵集合[W]’

把s套收率矩阵的集合记为[W]

[W]=[W(1),W(2),…,W(s)]

[W]’=[W].select(0≤W(t)_i≤1)

其中W(t)_i是W(t)中第i个进料的收率。

3. 计算[W]’中每套收率与Yc₁的MSE。

MSE=(Yc₁-X*W(t))²

使MSE最小的W(t)即为最佳收率矩阵Wr₁。

SPL例程

本例程介绍单出料的情况，多出料是一样的，只是多循环几次。

A5格利用迭代函数iterate(…)构造3^m种可能的取值标记。

A4中的标记表示3种可能情况，0表示需要最小二乘拟合，1表示下界，2表示上界。本例中有2列进料，会有9种标记组合，如下表：

A12格代码块计算出料Y的最佳收率矩阵W

计算结果示例：

先来看最小二乘法对上述X、Y的拟合结果：

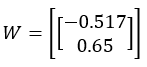
该收率W的MSE：

MSE=0.467

再来看有边界线性拟合算法的拟合结果：

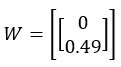
该收率W的MSE：

MSE=0.486

单纯比较MSE，最小二乘法的拟合结果更好，但因为不满足边界约束条件，不能应用在实际生产活动中，还是要选用有边界的线性拟合算法。