4.5 空间离散度
多维空间中的点可能是“聚集”的,也可能是散布在空间中的,怎么衡量空间中点分布的“离散程度”呢?
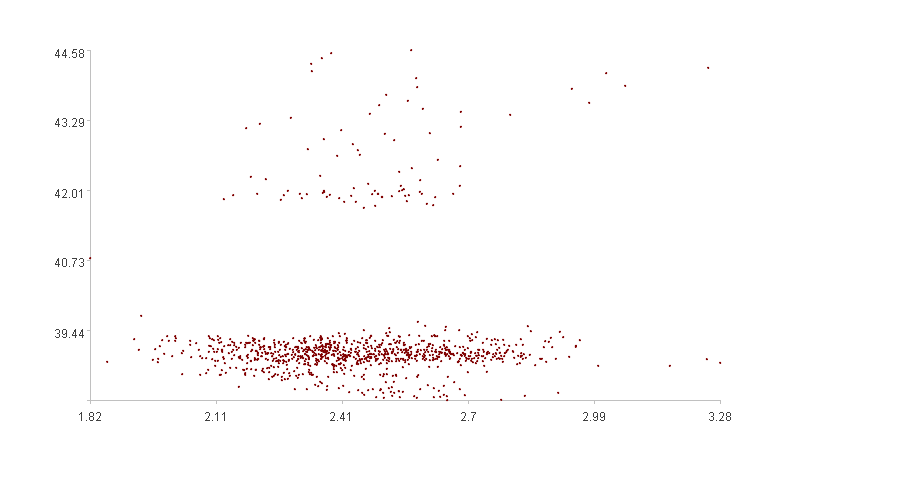
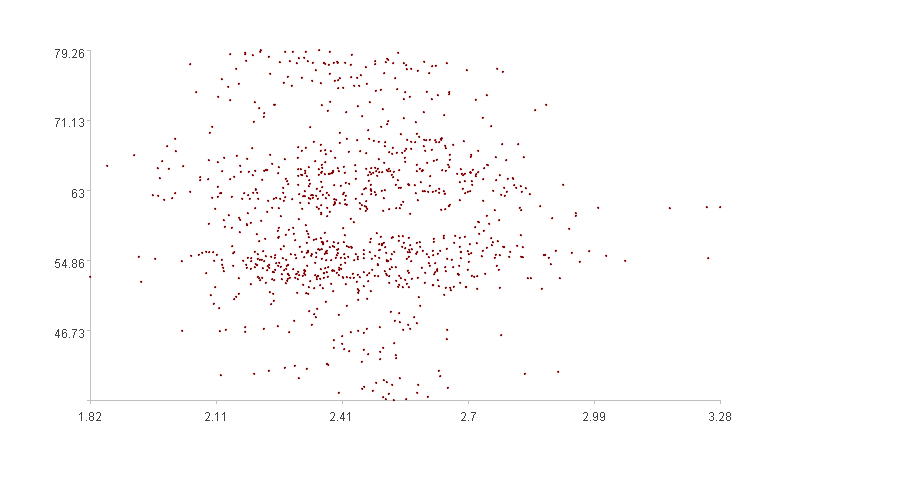
观察这两幅图,第一幅图有明显的聚集效应,多数点“聚集”在下方,少数点散布在上方,“离散程度”小;第二幅图聚集效应不太明显,分散在空间中的各个位置,“离散程度”大。
描述多维空间中点分布“离散程度”的量称为空间离散度。空间离散度越大,分布越离散,聚集效应越差。反之则分布集中,聚集效应越明显。
空间离散度可以这样描述:将多维空间切成若干个小空间,当点均匀落在这些小空间时,空间离散度大;当点集中落在某几个小空间中时,空间离散度小。
信息熵是描述信息源各可能事件发生的不确定性的量,不确定性越大,信息熵越大,不确定性越小,信息熵越小;空间离散度是描述点落入小空间可能性差别大小的量,落入各小空间的可能性差别越小(不确定性越大),空间离散度越大,落入各小空间的可能性差别越大(不确定性越小),空间离散度越小,因此可以用信息熵计算公式来计算空间离散度。
H(U)=sum(-P(u)*log2(P(u))),u∈U
其中H(U)是信息熵,U是所有事件的集合,u是某个事件,P(u)是事件u发生的概率。
多维时间序列X
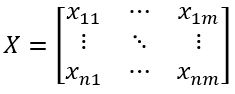
1. 均分各维度
将各维度平均切成h段,整个空间会被分为hm个小空间。
P(j)=[p(j)1, p(j)2,…, p(j)h]
p(j)l=min(Xcj)+(max(Xcj)-min(Xcj))/h*(l-1),l∈[1,h]
其中P(j)是第j维时间序列的切分点序列,p(j)l是均分Xcj的第l个切分点值。
2. 按切分空间为点标记位置信息
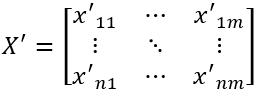
xij’= P(j).pseg(xij)
其中xij’是xij在P(j)中的位置。比如p(j)1≤xij< p(j)2,则xij’=1,说明xij属于在第j维度属于第1小段。
3. 统计同一小空间中点的个数
Sp=X’.group(~)
spds=count(sps)
其中Sp是有点落入的空间组,一个组就是1个小空间,spds是第s个组sps中点的个数。我们知道切分的总空间数是hm个,但可能有些空间没有点落入,所以通常情况下Sp内的组数是小于hm的。
4. 点落入各小空间的概率
把各空间落入的点数占总点数的比例作为落入该小空间的概率。
spps= spds/n
其中spps是落入第s个组的点数占总点数的比例。
5. 信息熵
etp=sum(-spps *log2(spps))
6. 空间离散度
信息熵有个特点,有点落入的空间组数越多,信息熵越大。通常情况下各维度切分的小空间数越多,有点落入的空间组数就越多,在单维度分段数相同的情况下,维度数越多,小空间数就越多,这导致维度数越多,信息熵越大。为了消除维度数对信息熵的影响,我们除以一个与维度相关的值就可以把维度数对信息熵的影响消除,把消除影响的值作为空间离散度。
dsp=etp/-log2(1/n)
SPL例程
A |
B |
|
1 |
=file(“DSP0.csv”).import@tci() |
/第一维数据 |
2 |
=file(“DSP1.csv”).import@tci() |
/第二维数据 |
3 |
10 |
/维度切分数 |
4 |
=[A1,A2] |
/XT |
5 |
=A4.(~.max()) |
|
6 |
=A4.(~.min()) |
|
7 |
=A6.((idx=#,m=(A5(#)-~)/A3,mi=~,A3.(mi+m*(#-1)))) |
/P(j) |
8 |
=A4.((idx=#,~.(A7(idx).pseg(~)))) |
/X’T |
9 |
=transpose(A8) |
/X’ |
10 |
=A9.group(~) |
|
11 |
=A10.(~.len()/A9.len()) |
/概率spps |
12 |
=-A11.sum(if(~==0,0,~*lg(~,2))) |
/信息熵 |
13 |
=n=power(A3,A4.len()),A12/(-lg(1/n,2)) |
/空间离散度 |
计算结果示例:


第一幅图是“DSP0.csv”和“DSP1.csv”两个维度数据呈现的二维图,计算出的空间离散度是0.560。
第二幅图是“DSP0.csv”和“DSP2.csv”两个维度数据呈现的二维图,计算出的空间离散度是0.818。
计算的结果和我们直观的感受一样,第二幅图空间离散度大于第一幅图。



