单维度异常发现算法能够得到单个时间序列的报警强度，通过某种方法对多个维度的报警强度进行“聚合”，就能得到多维时间序列的报警强度。我们仍然介绍简单朴素的方法来完成“聚合”，那就是对各维度加权平均。

AW_i=sum(Wr_i**Hr_i)

其中AW_i是第i个时刻的的聚合报警强度，Wr_i是第i个时刻m维时间序列的单维算法得到的报警强度，Hr_i是第i个时刻m维时间序列对应的权重。

权重从何而来？

（一）工艺知识

工业生产中存在大量的工艺知识，相互关联的时间序列中，哪个更重要，哪个不重要，在工艺知识中会有所涉及，查阅这些资料或者询问工艺专家，是可以得到相对准确的权重的。

（二）算法计算

当然，工艺知识不可能特别全面，从历史数据中学习权重是更可靠的办法。不过在介绍权重计算方法前先来看一个故事。

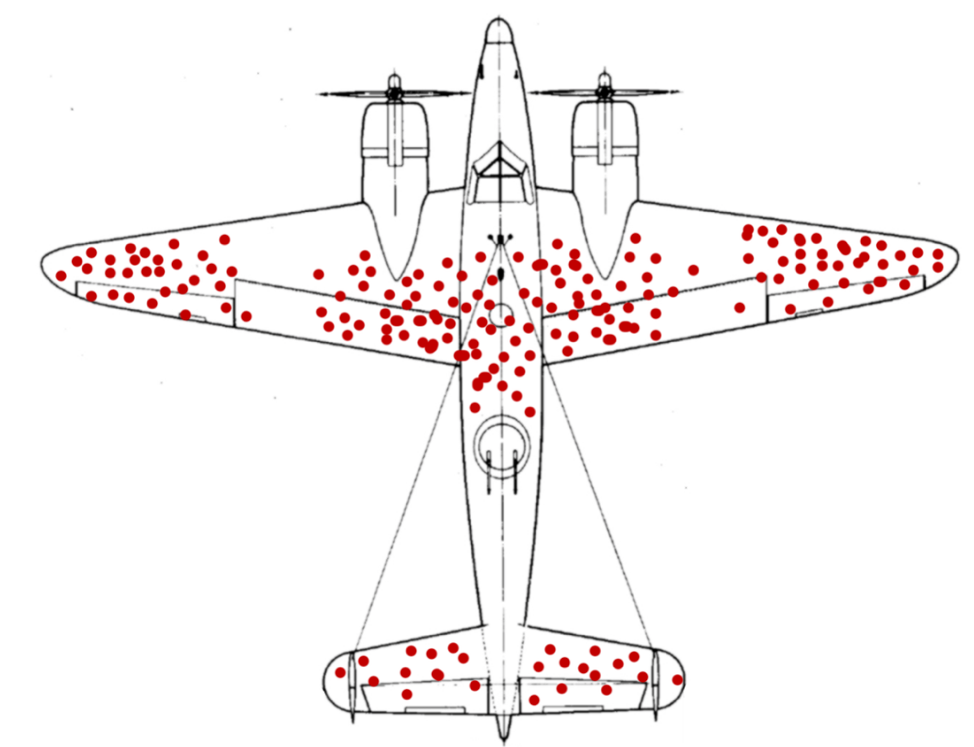
上图是二战时盟军返航飞机弹孔分布图，从图中可以看到，这些弹孔分布并不均匀，翅膀上比较多，引擎上比较少。当时军方普遍认为，应该减少装甲总量，然后在受攻击最多的部位增加装甲，这样飞机可以轻一点，但是防护作用不会减弱，因为防御的效率提高了。但是，这些部位需要增加多少装甲，他们并不清楚，于是找到瓦尔德（哥伦比亚大学的统计研究学家），希望得到答案。但是，瓦尔德彻底否定了他们的想法，给出了相反的答案。

瓦尔德认为，需要加装装甲的地方不应该是留有弹孔的地方，反而是没有弹孔的地方，即飞机的引擎。

瓦尔德讲，飞机各部位被击中的概率应该是均等的，但是引擎上的弹孔却比其余部位少，这说明那些被击中引擎的飞机根本没有机会返航。我们看到的数据，都来自成功返航的飞机，这说明即便翅膀被打得千疮百孔，仍能安全返航。

军方马上按照瓦尔德的建议改进了飞机，取得了良好的效果。

这就是“幸存者偏差”。我们不能只考虑看到的数据（返航的飞机），更应该考虑看不到的数据（未返航的飞机）。

为了避免幸存者偏差，多维时间序列权重的分配方法应该遵循这样的原则：历史上经常发生报警且报警强度大的维度（相当于机翼）权重小，不常发生报警且报警强度小的维度（相当于引擎）权重大。

多维时间序列X

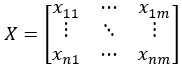
X中每一行Xr_i是某个时刻各个维度时间序列的值，每一列Xc_j是一个时间序列。

利用单维度异常发现算法E(…)计算得到各个维度的报警强度矩阵W，我们已经知道W中的元素可能大于1，而且理论上可以是无穷大，为了避免某个很大的数值影响到整体的计算，再考虑到报警强度为1时就已经表示强度很大了，所以将W中大于1的元素强制等于1。

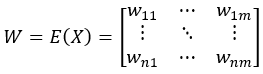
w_ij=if(w_ij>1,1,w_ij)

每个时刻都有一个权重序列，即权重也是个矩阵H：

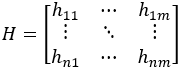
当前时刻的权重Hr_i是用之前一个区间的报警强度Wr[-k]_i计算得到的，即：

Hr_i=F(Wr[-k]_i)

其中F(…)是根据前面原则计算权重的方法。

现在我们来研究F(…) 的具体计算方法，即如何计算第i个时刻的权重序列Hr_i。

令Z =W[-k]_i

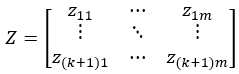
其中z_ij是Z第i个时刻第j个维度的报警强度。

1. 计算总报警强度SZ：

SZ=[sz₁,sz₂,…,sz_m]

sz_j=sum(Zc_j),j∈[1,m]

sz_j是SZ的第j个维度的总报警强度。

2. 计算第i个时刻的权重Hr_i：

每个时刻都能得到一个权重序列SZ。

SZ=[sz₁,sz₂,…,sz_m]

假设Hr_i=Y

Y=[y₁,y₂,…,y_m]

其中y_j是第j维时间序列的权重。

为了避免“幸存者偏差”，sz_j越大，y_j越小。对SZ中的元素求倒数再做线性变换就能得到权重Y。

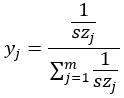
SZ中可能所有元素都是0，即所有维度都没有报警，强制令各维度权重相等，SZ中还可能部分元素是0，即sz_j可能是0，没有倒数，可以强制令它的倒数等于SZ中最大非0元素倒数的2倍，考虑到这些，y_j需要调整一下：

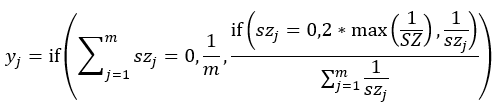
其中1/SZ是SZ中非0元素的倒数序列。

有了权重Hr_i，聚合报警强度AW_i就很容易计算了：

AW_i=sum(Wr_i**Hr_i)

SPL例程

计算结果示例：

两个维度的报警强度图：

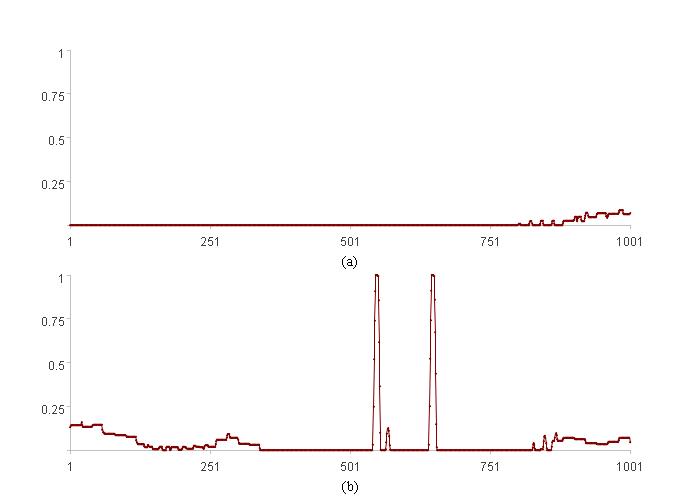
图中横轴都是索引，纵轴是报警强度。

图(a)(b)分别是第一维度和第二维度的报警强度走势图。从图中可以看出学习区间([1,1000])内，第二维度相较于第一维度的报警强度次数多且强度大，权重应该小。例程中计算出的权重也符合预期，分别是0.88和0.12。

最后一个点即当前时刻的聚合报警强度是0.065。