上一节中介绍的异常发现方法是将“聚集”在一起的点视为常见点，“分散”的点视为异常点，“聚集”通常是无规则的，只要在多维空间中距离近的点就算“聚集”。不过，有时我们会发现某些场景的“聚集”会有强烈的规则性，如下图：

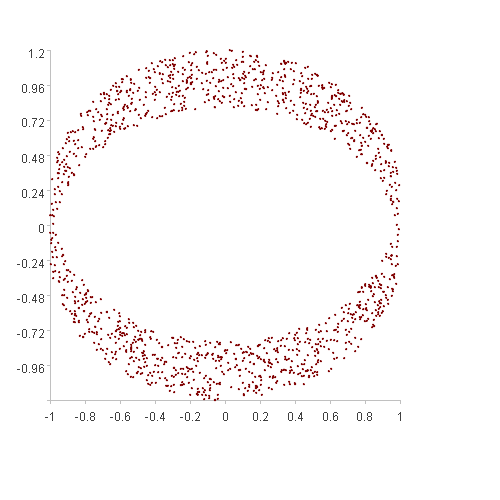
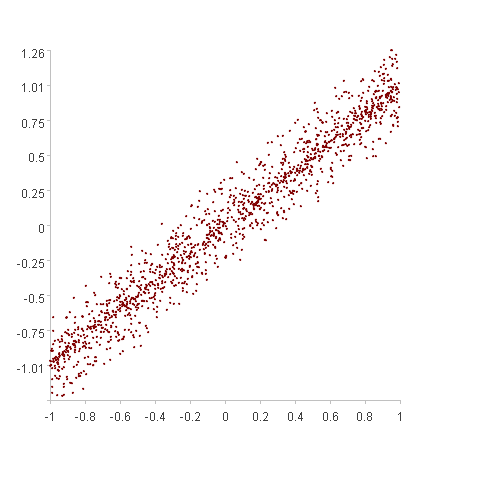
两张图都是基于某种规则聚集的，但使用上节介绍的空间距离法效果不会太好，会有很多的误报或漏报。

这类能看出“聚集”规则的多维时间序列可以利用规则计算出衍生序列，将多维时间序列发现异常的问题转化为衍生出的单维时间序列异常发现问题。

多维时间序列X

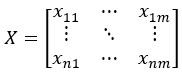
通过某种数学变换Dv(…)，衍生出单维时间序列D

D=Dv(X,…)

对D做单维时间序列异常发现，得到异常度序列Od

Od=Sg(D,…)

以最常见的线性聚集型二维时间序列为例介绍衍生方法。

二维时间序列X

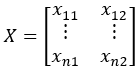
Xc₁和Xc₂整体可能是非线性的，但在一段比较小的区间内Xr[-k]_i近似是线性的，可以这样衍生：

1. 在Xr[-k]_i内通过最小二乘法拟合得到系数w_i

令Z=Xr[-k]_i

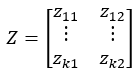
w_i=linefit(Zc₁,Zc₂)

2. w_i和当前点x_i1计算得到x_i2的预测值x’_i2

x’_i2=w_i* x_i1

3. 真实x_i2和x’_i2的差值就是衍生值df_i

df_i= x_i2-x’_i2

衍生列Df就是df_i的集合，df_i与Xr_i一一对应。

Df=[df₁,df₂,…,df_n]

SPL例程

A6是最小二乘法算w_i的过程

A8是计算预测值x‘_i2的过程

计算结果示例：

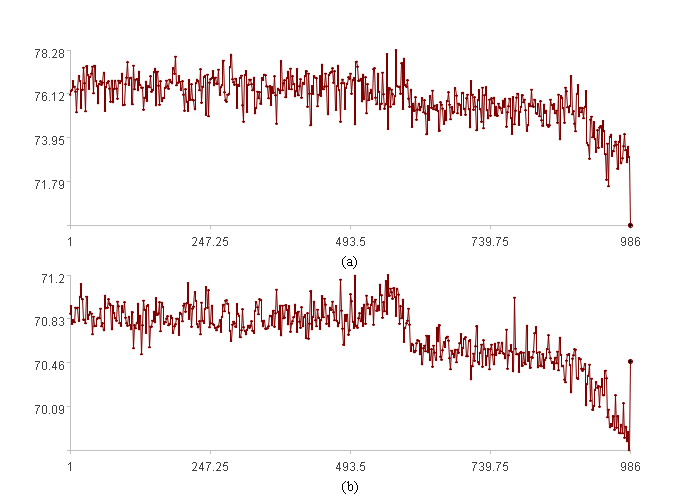
第一幅图是二维时间序列的走势图，其中。横轴是时间序列索引，(a)中纵轴是Xc₁，(b) 中纵轴是Xc₂，加粗点是待观测点；

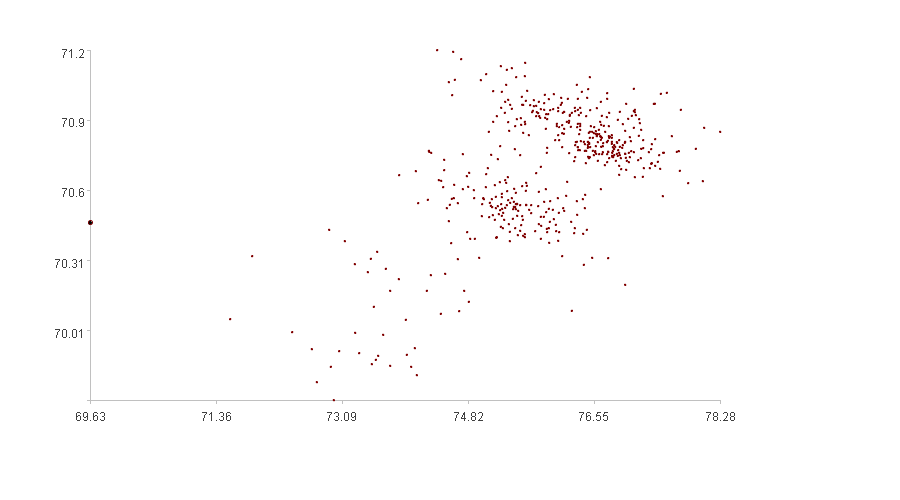
第二幅图是二维时间序列的关系图，横轴是Xc₁，纵轴是Xc₂，加粗点是待观测点。

观察右图，两个序列呈线性相关趋势，但待观测点明显不在线性“聚集”区，视为异常；观察左图的曲线走势，两者基本是同增同减，而带观测点却出现了Xc₁减，Xc₂增的反常情况，而且幅度还很大，同样视为异常。

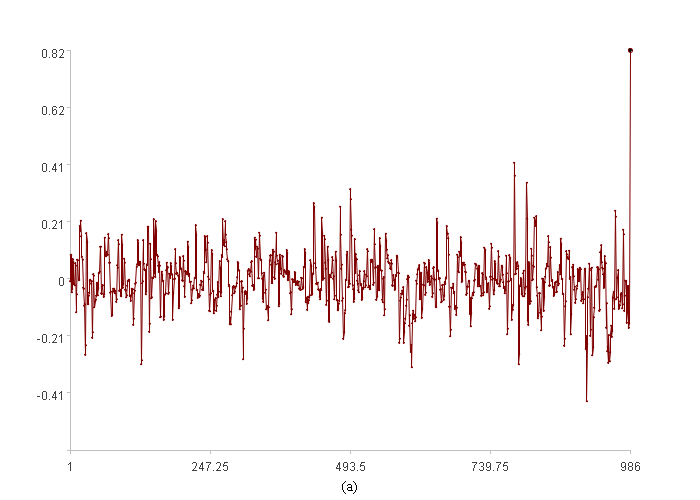
上图是衍生列的走势图，横轴是时间序列索引，纵轴是衍生列取值，加粗点是待观测点（前k个点没有衍生值，所以总数少k个点）。

观察上图中的衍生列，观测点衍生值非常大，我们已经知道这种值非常大的点是会被单维度异常发现算法发现的。仔细观察上图，凡是特别大或者特别小的点都可以对应原二维时间序列的异常走势。