4.2 多维联合
4.2.1 数据标准化
多维时间序列中各维度的量纲可能不同,计算距离前需要将各维度标准化到同样的量纲条件下,这种将不同量纲的数据转换成统一量纲的数据转换方法称为数据标准化。统计学有很多种数据标准化方法,本书中常用其中两种:最大最小值标准化(Max_Min)、标准分数(Z-score)。
做个简单回顾:
1. 最大最小值标准化(Max_Min)
最大最小值标准化是对原始数据进行线性变换,设mi和ma分别为序列A的最小值和最大值,将A的任一原始值ai映射成在区间[0,1]中的值a’i。
序列A
A=[a1,a2,…,an]
最大值ma和最小值mi
ma=max(A)
mi=min(A)
Max_Min标准化
a’i=(ai-mi)/(ma-mi)
SPL例程
A |
B |
C |
|
1 |
[2,4,2,5,10] |
/序列A |
|
2 |
=A1.max() |
||
3 |
=A1.min() |
||
4 |
=d=A2-A3,A1.((~-A3)/d) |
/标准化结果 |
|
2. 标准分数(Z-score)
标准分数标准化基于原始数据的均值(Ag)和标准差(σ)进行数据的标准化,将序列A的原始值ai标准化到a’i。
序列A
A=[a1,a2,…,an]
均值Ag和标准差σ
Ag=avg(A)
σ=std(A)
Z-score标准化
a’i=(ai-Ag)/ σ
SPL例程
A |
B |
C |
|
1 |
[2,4,2,5,10] |
/序列A |
|
2 |
=A1.avg() |
||
3 |
=sqrt(var@s(A1)) |
/标准差 |
|
4 |
=A1.((~-A2)/A3) |
/标准化结果 |
|
4.2.2 计算距离
1. 欧式距离
欧式距离(欧几里得距离euclidean metric)是一个通常采用的距离定义,指在m维空间中两个点之间的真实距离。
m维数据点A,B
A=[a1,a2,…,am]
B=[b1,a2,…,am]
两点之间的欧式距离d:
d=sqrt(sum((ai-bi)2))
SPL例程
A |
B |
C |
|
1 |
[3,5,4,12,9] |
/点A |
|
2 |
[5,15,5,6,7] |
/点B |
|
3 |
=dis(A1,A2) |
/欧式距离 |
|
2. 马式距离
马氏距离(Mahalanobis Distance)是数据的协方差距离,可以看作是欧氏距离的一种修正,修正了欧式距离中各个维度尺度不一致且相关的问题。
m维矩阵Y:
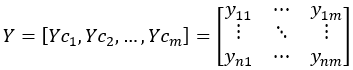
任意两列Yci和Ycj的协方差Cov(Yci, Ycj)
Cov(Yci, Ycj)=sum((yki-avg(Yci))* (ykj-avg(Ycj)))/(n-1),k∈[1,n]
其中yki是第Y的第k行的第i个元素。
协方差矩阵Σ
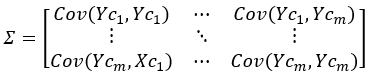
Y中两点Yri、Yrj的马氏距离d
d=sqrt((Yri-Yrj)T*Σ-1*(Yri-Yrj))
观察上式可以发现,当协方差矩阵Σ是单位矩阵时,马氏距离等于欧式距离。当Σ不可逆时,无法计算马氏距离。
SPL例程
A |
B |
C |
|
1 |
[[3,5],[5,15],[4,5],[12,6],[9,7]] |
/全部样本 |
|
2 |
[3,5] |
/点A |
|
3 |
[4,5] |
/点B |
|
4 |
=covm(A1) |
/协方差矩阵 |
|
5 |
=dism(A2,A3,A4) |
/马氏距离 |
|
欧式距离和马氏距离各有优劣,详情见下表:
优 势 |
劣 势 |
|
欧式距离 |
计算简单,不受整体样本分布影响。 |
同等看待不同属性,受量纲影响大。 |
马氏距离 |
不受量纲影响; 排除了变量间的相关性的干扰 |
受全体样本分布影响,同样的两点,在不同的样本分布情况下,协方差不同,所以距离也不等; 协方差必须可逆,否则无法计算马氏距离; |
4.2.3 发现异常
令Z= Xr[-(k+1)]i+1,Z是一个(k+1)*m矩阵,其中k是Xri之前一个区间的长度。
1. 矩阵Z所有点两两计算距离
(1) 欧式距离
① 对列标准化
a. Max_Min标准化
Xcj’=Max_Min(Zcj)
b. Z_score标准化
Xcj’=Z_score(Zcj)
其中Zcj’是标准化后的矩阵Z’的第j列元素。Max_Min(…)是Max_Min标准化函数,Z_score(…)是Z_score标准化函数。
② 所有点两两算距离形成距离矩阵DisM
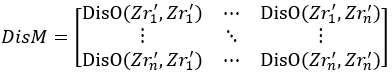
其中DisO(…)是计算欧式距离的函数。
(2) 马氏距离
① 马氏距离不需要标准化
Z’=Z
② 计算距离矩阵DisM
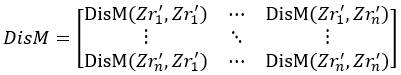
其中Dis![]() (…)是计算马式距离的函数。
(…)是计算马式距离的函数。
2. 多维空间最远距离mdis。
多维空间中,所有维度的最大值与所有维度的最小值之间的距离最远。
所有维度都是最大值的点坐标:
MaD=[max(Zcj’),j∈[1,m]]
所有维度都是最小值的点坐标:
MiD=[min(Zcj’),j∈[1,m]]
最远距离mdis
欧式距离:
mdis=DisO(MaD,MiD)
马式距离:
mdis=DisM(MaD,MiD)
3. 标准半径r
r=mdis*r_per
其中r_per是半径百分比,作为变量输入,标准半径的范围就是“周围”。
4. 每个点“周围”的点数Dn
dnl=count(DisMrl<r)
其中dnl是Z中第l个点周围的点数,DisMrl是距离矩阵DisM第l行的元素。
5. 标准点数sn
sn=Threshold(Dn,arg)
其中Threshold(…)是阈值计算函数,可以选择箱线图法、正态统计法、法计算,取阈值下限作为标准点数。注意:参数arg要与相应方法对应,如箱线图法要设置分位距倍数,正态统计法要设置标准差倍数,距离计算阈值要设置参数半径倍数。
6. 异常度od
od=if(dnk+1≥Sn,0,(sn-dnk+1)/sn)
Z中第k+1个点就是X中的第i个点,dnk+1是Z中第k+1个点周围点数,od是第k+1个点的异常度。
A |
B |
|
1 |
=file(“2DPlot_data0.csv”).import@tci().to(1000) |
/第一维数据 |
2 |
=file(“2DPlot_data1.csv”).import@tci().to(1000) |
/第二维数据 |
3 |
=r_per=0.25 |
/半径比例r_per |
4 |
=r_n=3 |
/距离法参数半径倍数 |
5 |
=[A1,A2] |
/二维数据 |
6 |
=A5.(Max_Min(~)) |
/最大最小值归一化 |
7 |
=transpose(A6) |
/转置 |
8 |
=A7.((idx=#,d=~,A7.m(:idx-1,idx+1:).(dis(~,d)))) |
/距离矩阵DisM |
9 |
=A6.(~.max()) |
|
10 |
=A6.(~.min()) |
|
11 |
=dis(A9,A10) |
/最远距离mdis |
12 |
=A11*r_per |
/标准半径r |
13 |
=A8.(~.count(~<A12)) |
/周围点数Dn |
14 |
=Threshold(A13,"down",r_n) |
/距离法计算标准点数sn |
15 |
=d=A13.m(-1),if(d>=A14,0,1-d/A14) |
/异常度od |
上述介绍的标准化方法、距离计算方法、阈值计算方法都可以更换,根据实际场景选择更好的方法,设置更合适的参数,适应更多的工业场景。
计算结果示例:
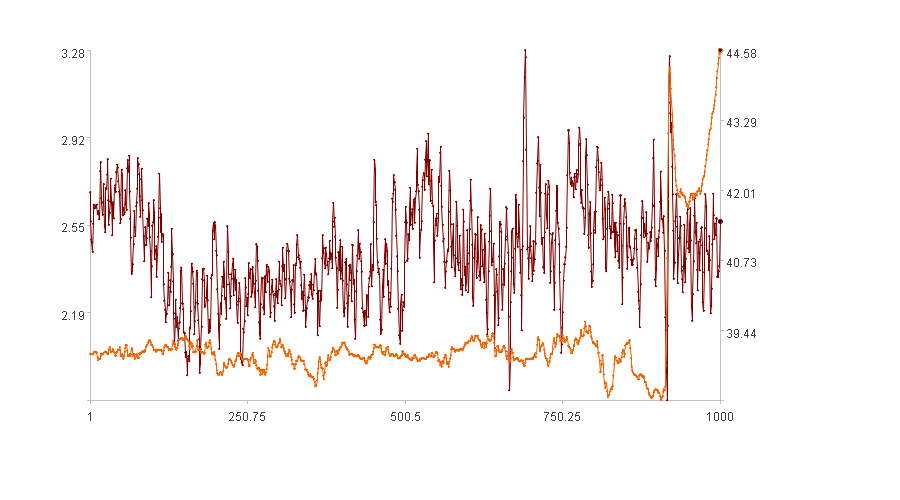
第一幅图是两个时间序列的走势图,横轴是序列索引,左纵轴是第一维度取值,右纵轴是第二维度取值,加粗点是第k+1个点的取值(k=999)。
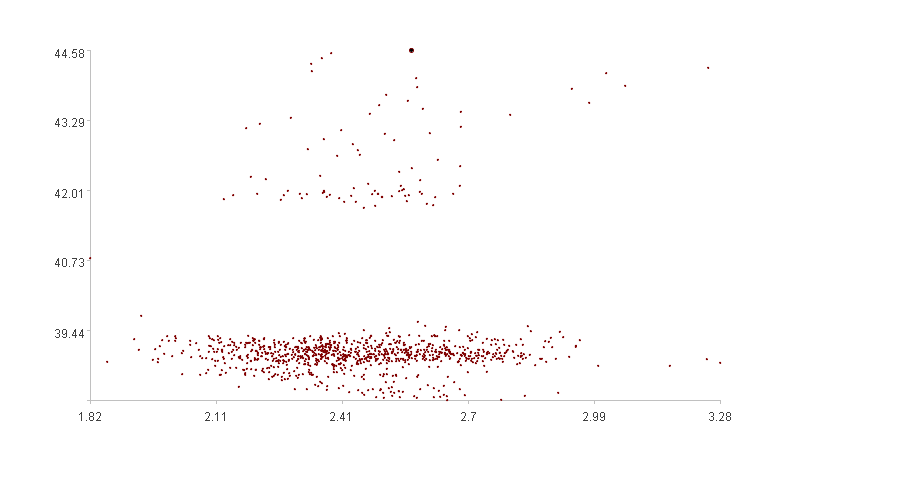
第二幅图是两个时间序列的散点图,横轴是第一维度取值,纵轴是第二维度取值,加粗点是第k+1个点。
右图二维散点图可以看出,第k+1个点属于异常点,这也正好符合算法算出来的异常度0.93。



