工业生产中，可能会有两个或者多个仪表协同工作的情况，如温度和压力，阀门开度和流量等。把多个时间序列形成的序列称为多维时间序列，用矩阵X表示。

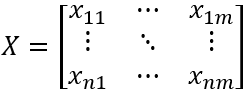
X是m维时间序列，它的第i行是m个时间序列第i个时刻的取值，记为Xr_i。

Xr_i=[x_i1,x_i2,…,x_im],i∈[1,n]

X由n个时刻的Xr_i组成：

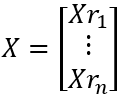
X的第j列是第j个单维时间序列，记为Xc_j。

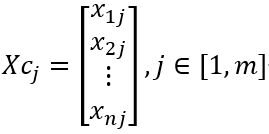
X由m个Xc_j组成：

X=[Xc₁,Xc₂,…,Xc_m]

多维时间序列的异常发现可以延用单维异常发现的原则和方法。仍然是认为没出现过或者不常出现的数据是异常，还是采用无监督学习的方法，只是从观察单序列扩展到多序列，也就是把多维时间序列X的一行看成一个样本，相当于多维空间中的一个点。从几何的角度看，此时的异常发现就从单维空间扩展到了多维空间，但模式仍然和单维空间相同，即看当前时刻数据Xr_i相较于之前一段区间数据Xr[-k]_i是否不常出现，通过Xr[-k]_i学习出一个判断Xr_i是否不常出现的模式E(…)，用E(Xr_i)的返回值判断Xr_i是否不常出现。

模式E(…)的函数理论上有无穷多，这里还是抛砖引玉，列举一类常用方法发现多维时间序列异常。

m维时间序列X的每个时刻都是m维空间中的一个点，以某种方式“聚集”在一起的点可以认为是经常出现的点，“分散”在空间中的点被认为是不常出现的点，即异常点。

为了看的更直观，以二维情况为例，画出时间序列的走势图和这两个维度形成的散点图。

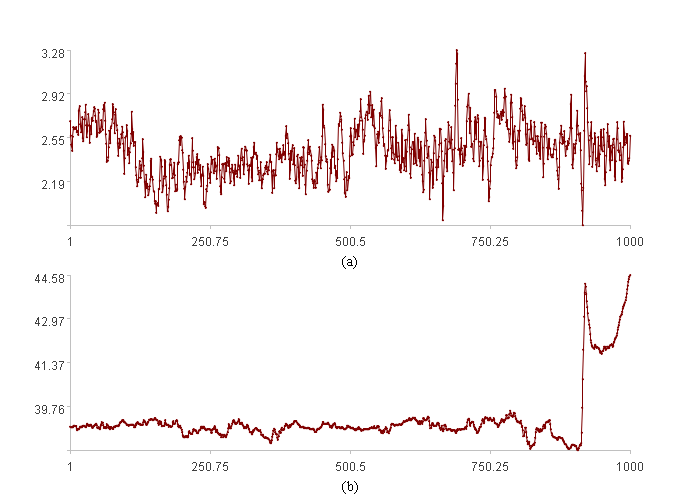
左图是两个时间序列各自的走势图（横轴是位置索引，纵轴是各自的取值）。

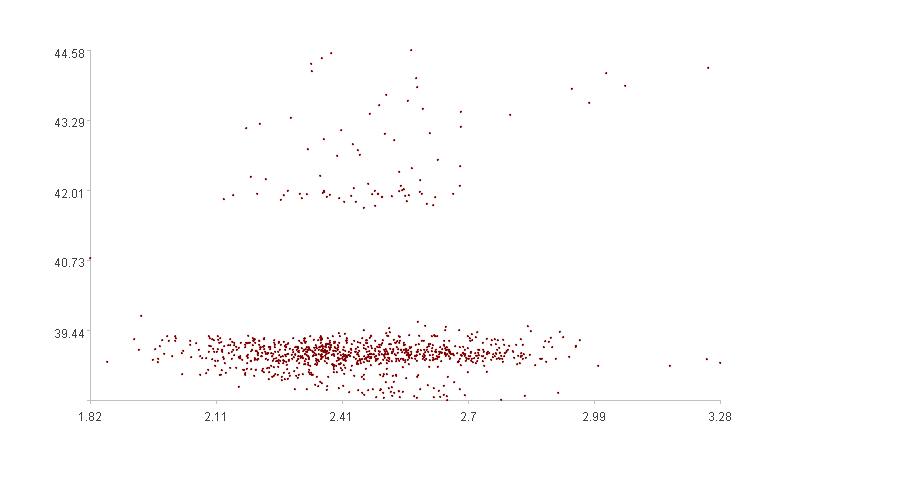
右图是两个时间序列组成的二维时间序列在二维空间中的散点图（横轴是时间序列一的值，纵轴是时间序列二的值）。

从左图很难看出有什么规律，但右图则可以明显地发现，多数点聚集在一起，少数点分散在空间中，只要找到一个模式E(…)把分散在空间中的点找出来即可。

聚集在一起的点“周围”的点数多，分散在空间中的点的“周围”点数少，统计每个点“周围”有多少个点，再设定一个标准，当“周围”点数多于标准时，认为是正常数据，异常度是0；少于标准时认为是异常，相比标准差的越多，异常度越大。

例如：E(…)可以是这样一类函数TA[a₁,a₂,…](…)：

TA[S,R](xr_i)=if(N≥S,0,(S-N)/S)

其中S是“周围”标准点数，R是“周围”的半径,N是当前点Xr_i的“周围”点数，S、N都是通过Xr[-(k+1)]_i+1和R计算得到的。