2.2 变化率
变化率是描述原值变化快慢的衍生序列。
通俗地看,变化率可以简单地用时间序列原值在单位时间内的变化差值来表示,变化率C可以这样计算:
ci=(xi-xi-l)/l
当l=1时就是原值的差分序列,这种方法我们也可以称为差分方法。
差分方法只使用了区间两端的值,而忽略了区间中间的值,这种方法不能很好地描述整个区间的性态。我们还可以用最小二乘拟合的方法来定义变化率,这样就可以描述整个区间的性态了。即对X[-(l+1)]i+1进行一元线性回归,把回归得到的直线斜率作为xi的变化率。
ci=(n*sum(j*xj)-sum(j)*sum(xj))/(n*sum(j2)-sum(j)2),j∈[1,n]
其中n是X[-(l+1)]i+1的长度n=l+1,xj是X[-(l+1)]i+1中的第j个元素。
SPL例程:
A |
B |
C |
|
1 |
=data=file(“1Ddata.csv”).import@tci().to(100) |
/时间序列X |
|
2 |
=l=5 |
/区间l |
|
3 |
=data.((if(#<=l,null,(s=~[-l:0],func(A4,s))))) |
/变化率C |
|
4 |
func |
/计算变化率ci的方法 |
|
5 |
=n=A4.len() |
/n |
|
6 |
=n*A4.sum((j=#,xj=~,j*xj)) |
/n*sum(j*xj) |
|
7 |
=A4.sum((j=#,j))*A4.sum((xj=~,xj)) |
/sum(j)*sum(xj) |
|
8 |
=n*A4.sum((j=#,j*j)) |
/n*sum(j2) |
|
9 |
=m=A4.sum((j=#,j)),m*m |
/sum(j)2 |
|
A3格中计算变化率C,因为l=5,X中前5个元素不具备计算变化率的条件,所以令其为空值null,其他xi则按拟合方法计算ci。
A4代码块就是线性回归的计算过程。
计算结果示例:
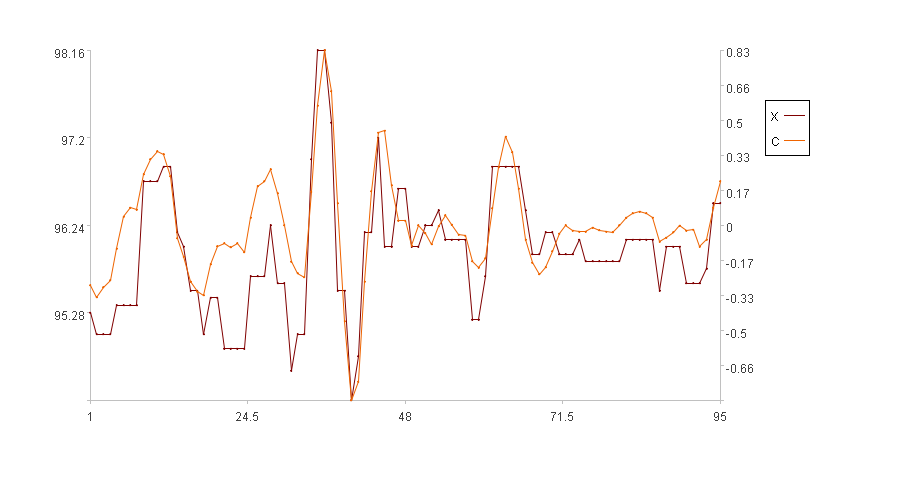
图中横轴是序列索引,左纵轴是原值X的取值,右纵轴是变化率C的取值。图例中X是原值,C是变化率。(前5个时刻没有变化率,图中只画了后95个时刻的变化率)



