1.1 时间序列与异常发现
时间序列是指某个观察指标的数值按其发生的时间先后顺序排列而成的数列。如工业上电表每秒测出的电压、每个小时油料的流量、产品每天的产量等,这些都是时间序列。
在统计研究中,常用按时间顺序排列的一组变量来表示时间序列,简记为Xt。
Xt=[xt(0), xt(1),…, xt(n)]
其中t(i)代表第i个时刻,xt(i)是第i个时刻的取值,n称为时间序列Xt的长度。
时间序列的发生时刻通常是等间隔的,即序列[t(i),…]是等差数列。这种平凡的数列不需要特别关注,我们经常就用序号来代替表示时刻的t(i)序列。以后行文中如未特殊说明,时间序列Xt将记为:
X= [x1,x2,…,xn]
其中xi是第i个时刻的取值。
X中某个时刻之前或之后的一段数据称为区间数据,简称为区间。区间是时间序列X的一个连续子集,也是一个时间序列。
xi之前一个区间长度为k的数据记为X[-k]i:
X[-k]i=[xi-k, xi-k+2,…, xi-2,xi-1]
xi之后一个区间长度为k的数据记为X[+k]i:
X[+k]i=[xi+1, xi+2,…, xi+k-1,xi+k]
xi和xi之前一个区间长度为k的数据记为X[-(k+1)]i+1。
发现时间序列中的异常值可以理解为某种数据挖掘任务,即把是否异常作为目标变量。但数据挖掘方法是一种有监督学习,即需要事先标记哪些是异常值。而时间序列的数据量通常很大,而且会随时间而变化,对大量历史数据进行准确及时的标记是不太现实的,因此不能用有监督的学习方法,只能使用无监督学习方法。
那么,无监督时,也就是不需要标记时,又该如何定义“异常”?
简单来说,我们可以认为大部分数据是正常的(否则工业生产不能正常进行),只有少数不正常。异常可以这样定义:没出现过或者不常出现的数据。这样,异常发现的问题就变成发现哪些数据不常出现。
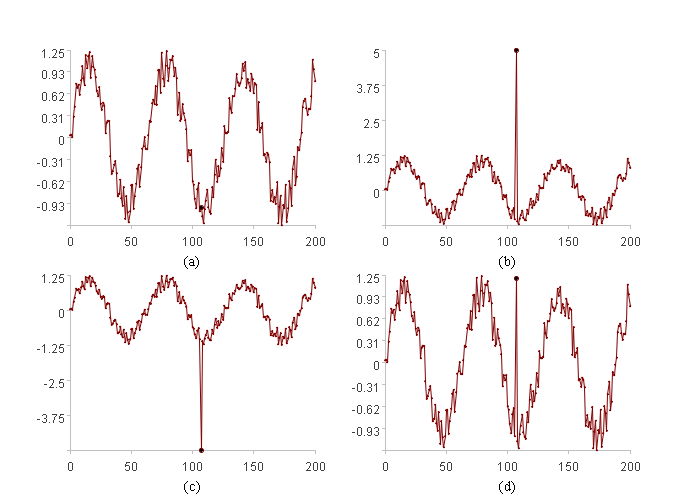
上图是同样的数据同样的位置(加粗点)出现了不同的情况,(a)属于正常数据,(b)因为过大属于异常,(c)因为过小属于异常,(d)的情况比较特殊,但它仍然不同于之前的情况,属于异常。总之,(b)(c)(d)都属于不常见数据,我们的目标就是发现它们。
判断数据是否不常出现,就是看当前数据xi相较于之前一段区间数据X[-k]i是否不常出现,可以通过X[-k]i学习出一个判断xi是否不常出现的模式。
所谓模式就是一个函数E(x),即用E(xi)的返回值判断xi是否不常出现,也就是是否异常。这样,异常发现的任务可以定义为:从历史数据X[-k]i学习出一个返回布尔值(真/假或0/1)的异常函数E。
显然,即使可写出计算式的函数的形式也太多了,我们不太可能尝试所有函数。实际可行的办法是先确定一些常用的函数形式,而待定其中的参数,通过X[-k]i学习出异常函数的任务其实只是确定参数。
严格一些的说法是这样:先选定某个确定形式和待定参数的函数族
E[a1,…](x)=f(ai,…,x)
其中f是个有明确形式的表达式,然后通过历史数据X[-k]i的学习确定这里的参数a1,…,从而确定这个函数。
比如这样一个函数:
TA[tu,td](x)=if(max(x-tu, td-x,0)>0,1,0)
其中tu、td分别是从X[-k]i中学习出来的某个阈值上限和阈值下限,在区间[td,tu]之间包含大部分常见数据,区间之外是不常见的异常数据。这样,TA[tu,td]函数返回1表示异常,0表示正常,它可以发现上图中(b)(c)中的异常。函数族TA[tu,td]有两个待定参数tu、td,使用某种方法通过X[-k]i来学习确定tu,td后,就可以把函数确定了。
TA[tu,td]可称为阈值型异常函数。我们以后还会设计更多形式的异常函数。
经验表明,在实际生产过程中,异常状态经常是渐变的,而不是突变的。这时,仅仅用真假值来描述是否异常就显得有些简单,而用一个连续值来衡量异常的程度则会获得更丰富的信息量。
这样,我们把异常函数E的返回值改成返回异常度,也就是异常的程度。它是一个实数,值越大表示“异常度”越大,大于0表示异常,0则表示正常。
比如对刚才举例的阈值型异常函数稍加改造就可以得到返回异常度的函数。
TA[tu,td](x)=max(x-tu, td-x,0)/(tu-td)
tu、td的含义没变,仍然从历史数据X[-k]i中学习获得。
根据我们发现异常的原则,常见的数据是正常的,不常见的数据是异常的,在设置k时,要使得每个时刻的X[-k]i中多数数据是正常的,只有少数或者没有数据异常。这就意味着当异常数据可能持续很长时间时,k要大一些,当异常数据持续时间比较短时,k要小一些,根据实际情况来设置合适的k。
另外,如果只用当前时刻之前一个区间的数据X[-k]i来学习,tu、td的极限分别是这段数据的最大值和最小值,如果当前时刻数据xi大于X[-k]i的最大值或小于最小值就一定被认为是异常,多数生产环境中这么判断没有问题。但在有些生产环境中,xi小幅度大于或小于之前数据时可以认为是正常,满足这种需求也很简单,只要让xi参与tu和td的计算,即用X[-(k+1)]i+1来计算tu和td,这样当xi不是特别大或者特别小时,有机会作为tu或td,这时就会认为xi是正常的。
假设时间序列当前时刻的值是xi,它之前一个区间的序列是X[-k]i,下面介绍一些常用的发现方法来计算xi的“异常度”。



