无监督实时异常发现算法
无监督实时异常发现算法
算法背景
实际生产中会定时产生一些数据(比如:炼油设备的压力、液位、电气设备的电流、电压等),称为时间序列。生产活动发生异常时,很可能会有前兆反映在这些时间序列中,也就可能在时间序列中出现一些异常值,如果我们能够把这些异常值甚至其异常程度实时计算出来,就能提前预警,避免事故的发生。
考虑到生产过程中的时间序列的特点,实现异常发现算法时,先要回答下述3个问题:
1. 用有监督学习还是无监督学习
生产活动中产生的数据量是巨大的,而且数据会随工况的变化而变化,仅仅是对大量历史数据标记就要耗费巨大的人力物力,而且工况变化后,标记的数据也就不能用了。因此不能用有监督的学习方法,只能使用无监督学习算法实时计算。
2. 无监督时,该怎样定义”异常”?
生产活动能够顺利进行,证明多数时间数据都是正常的,只有少数数据不正常,可以这样定义异常:没出现过或者不常出现的数据是异常。
3. 又该如何表达异常程度?
可以设计一个数学量来表达异常程度,我们将这个量称为报警强度。
报警强度需要有如下特征:
1. 异常程度越大时报警强度越大;
2. 连续异常时报警强度增大;
3. 距离当前时刻越远的异常点对当前时刻的报警强度影响越弱。
算法原理
针对上述的一些原则,我们先以时间序列中的原值来发现异常,用《剔除集合中过大过小的异常值》中的算法计算阈值上限和阈值下限,在阈值上下限之间的数据是多数数据,超限的数据是少数数据,也就是异常值,用超限幅度的累积情况来描述报警强度。后续会撰文介绍原值衍生出的其他特征来描述异常。
算法过程
时间序列用X表示
X=[x1,x2,…,xn]
其中xi是X的第i个元素,xi是ti时刻对应的取值。
1. 计算一个学习区间的阈值上下限
时间序列X可能很长,我们认为当前时刻的取值只和之前一个区间内的值有关系,将这个区间称为学习区间,记为learn_interval。下面介绍一个学习区间内各个量的计算方法,用XL表示一个长度为learn_interval的时间序列。
XL=[x1,x2,…,xlearn_interval]
(1) 计算极值
如果某个时刻的值大于之前一个区间的所有值且不小于之后一个区间的所有值,则称该值为极大值,这个区间称为极值区间,记为extrem_interval,极大值组成的序列称为极大值序列,记为MaxSeq。
MaxSeq=[xi,xi>max([xi-extrem_interval,…,xi-1])and xi≥max([xi+1,…,xi+extrem_interval])]
如果某个时刻的值小于之前一个极值区间的所有值且不大于之后一个极值区间的所有值,则称该值为极小值,极小值组成的序列称为极小值序列,记为MinSeq。
MinSeq=[xi,xi<min([xi-extrem_interval,…,xi-1])and xi≤min([xi+1,…,xi+extrem_interval])]
(2) 计算阈值上下限
《剔除集合中过大过小的异常值》算法中介绍了计算阈值上下限的方法,这里我们将计算阈值的方法称为阈值算法,用threshold()函数表示。
利用极大值序列计算阈值上限,记为up。
up=threshold(MaxSeq,”up”,2)
利用极小值序列计算阈值下限,记为down。
down= threshold(MinSeq,”down”,2)
MaxSeq和MinSeq是一个学习区间计算得到的极值序列。
2. 计算报警幅度
如果xlearn_interval+1大于它之前一个学习区间的阈值上限或者小于阈值下限,则认为该值超限,将原值与阈值上限的差或者阈值下限与原值的差称为超限幅度,记为ov_range。如果原值在阈值上下限内,则它的超限幅度是0。

将阈值上下限的差称为阈值差,记为threshold_diff。
threshold_diff=up-down
超限幅度与阈值差的比值称为报警幅度,记为warn_range。
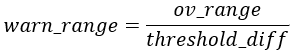
3. 计算报警强度
报警幅度在一个区间内的累积值称为报警强度,记为warn,累积区间称为报警间隔,warn_interval。
设xlearn_interval+1之前一个报警间隔内的报警幅度序列为WarnRange
WarnRange=[warn_range1,warn_range2,…,warn_rangewarn_interval]
距离越远的报警幅度对当前的报警强度影响越小,因此WarnRange在累积时应该有个衰减效应,可以使用对数函数来衰减。衰减后的报警强度序列记为WarnRange’
WarnRange’i= warn_rangei *log2*warn_interval(2*i)
learn_interval+1时刻的报警强度
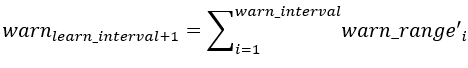
单纯的进行衰减累加,warn_interval越大,报警强度就会越大。报警间隔内所有值都异常且幅度都为1时,认为这段的报警强度很大,把它作为对比值,来计算报警强度。
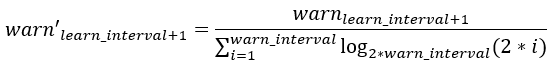
warn’learn_interval+1即为xlearn_interval+1的报警强度。
4. 移动窗口实时计算报警强度
以learn_interval为移动窗口,每次利用当前时刻之前的learn_interval个数据按照上述方式计算报警强度就可以实时发现异常值并计算它的报警强度。
写出代码
A |
B |
C |
|
1 |
=seq |
/输入参数:X |
|
2 |
=learn_interval |
/输入参数:学习区间 |
|
3 |
=extrem_interval |
/输入参数:极值区间 |
|
4 |
=warn_interval |
/输入参数:报警间隔 |
|
5 |
=func(A12,A1,A3) |
/极值序列 |
|
6 |
=func(A16,A5.(~(1)),A2,A3,A1,"up") |
/阈值上限 |
|
7 |
=func(A16,A5.(~(2)),A2,A3,A1,"down") |
/阈值下限 |
|
8 |
=func(A19,A6,A7,A1,A2) |
/报警幅度 |
|
9 |
=func(A23,A8,A4) |
/报警强度 |
|
10 |
return A9 |
||
11 |
/计算极值, 参数:序列,极值区间 |
||
12 |
func |
||
13 |
=A12.len() |
||
14 |
=A12.(if(#<=B12||#>B13-B12,[,],(ss=~[-B12:-1],es=~[1:B12],sma=ss.max(),ema=es.max(),smi=ss.min(),emi=es.min(),[if(~>sma&&~>=ema,~,if((ss|~|es).id()==[~]&&#%(2*B12)==0,~,)),if(~<smi&&~<=emi,~,if((ss|~|es).id()==[~]&&#%(2*B12)==0,~,))]))) |
/计算极大极小值,如果某个值的前后区间内的值都等于该值则每隔两个极值区间取个该值 |
|
15 |
/计算阈值上下限,参数:极大值序列,学习区间 |
||
16 |
func |
||
17 |
=f=threshold(A16.m(:B16-C16),E16,2),f=if(!f,threshold(D16.m(:B16-1),E16,2),f),A16.(if(#<=B16,,((ss=~[-B16+C16:-1-C16],f=if(ss.id()==[null],threshold(D16.m(#-B16:#-1),E16,2),if(~[-B16+C16-1]==~[-1-C16],f,threshold(ss,E16,2))))))) |
/如果单调很久就对全部值计算阈值上限 |
|
18 |
/计算报警幅度, 参数:阈值上限,阈值下限,原值,学习区间 |
||
19 |
func |
||
20 |
1e-5 |
||
21 |
=C19.(if(#<=D19,null,((u=A19(#),d=B19(#),diff=u-d,if(~>u,(~-u)/(if(diff<B20,~-u,diff)),if(~<d,(d-~)/if(diff<B20,d-~,diff),0)))))) |
/如果上限等于下限时,报警幅度等于 1 |
|
22 |
/计算报警强度,参数:报警幅度,报警间隔, |
||
23 |
func |
||
24 |
=func(A27,B23.(1),B23) |
/标准强度 |
|
25 |
=A23.((itv=~[-B23+1:0],itv=if(itv.len()<B23,(B23-itv.len())*[null]|itv,itv),func(A27,itv,B23)/B24)) |
||
26 |
/报警幅度衰减函数,参数:1 个报警间隔的报警幅度, 报警间隔 |
||
27 |
func |
||
28 |
=A27.sum(~*lg(2*#,2*B27)) |
/衰减累加 |
|
输入参数说明:
1. seq:输入序列
2. learn_interval:学习区间,如:100。
3. extrem_interval:极值区间,如:3。
4. warn_interval:报警间隔,如:20
应用举例
输入序列如下图:
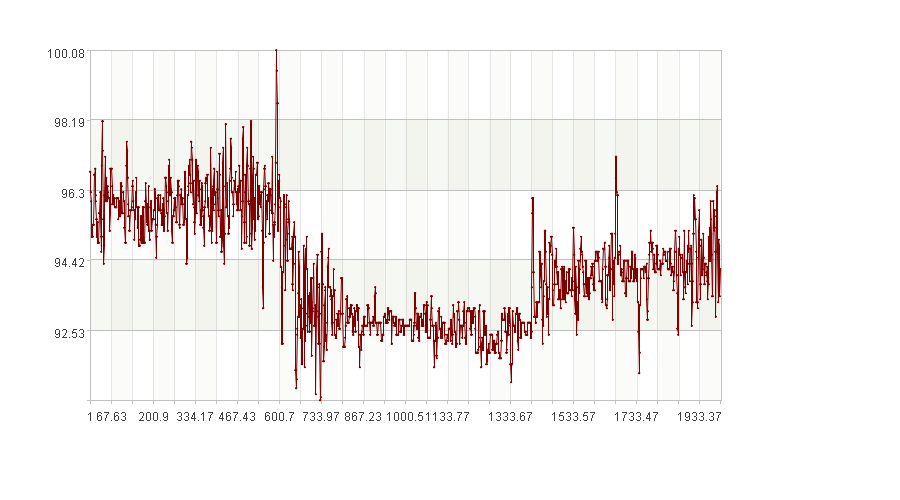
图中横轴是序列的索引,纵轴是序列中的值。
报警强度图如下:
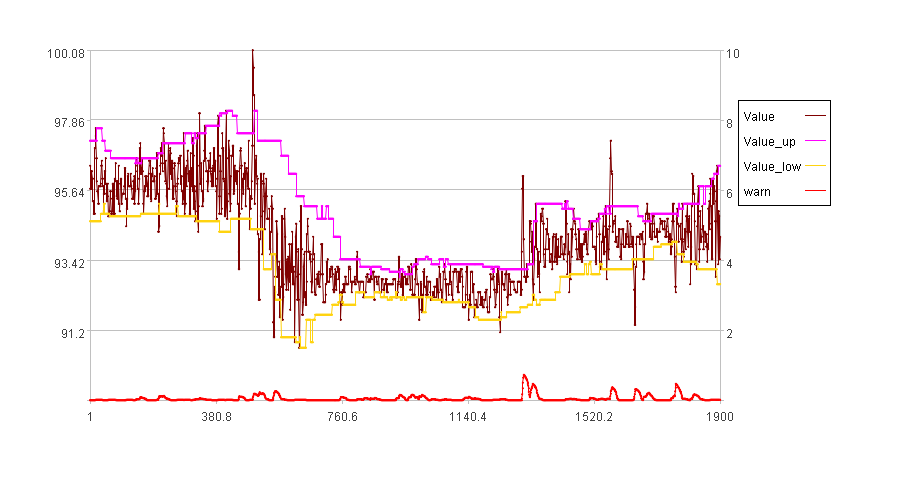
因为前100个数据是学习数据,所以不计算报警强度,上图中的红线是后1900个数据的报警强度曲线。



