算法背景

之前介绍了有边界的线性拟合算法，《有边界的线性拟合算法》，它的约束条件是所有系数都须在[0,1]范围内，但实际生产环境不仅仅是这个基本的限制。

已知条件

自变量矩阵X，在生产环境中称为进料矩阵：

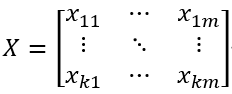
X是k*m矩阵，k是样本数，m是自变量数，x_ij是第i个样本的第j个自变量。

因变量矩阵Y，在生产环境中称为出料矩阵：

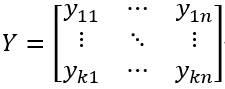
Y是k*n矩阵，k是样本数，n是因变量数，y_ij是第i个样本的第j个因变量。

基础系数矩阵B，在生产环境中称为基础收率：

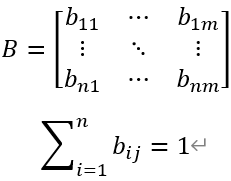
B是n*m矩阵。b_ij是第i个因变量（进料）第j个自变量（出料）的基础收率，基础收率的列和等于1。

边界矩阵BD

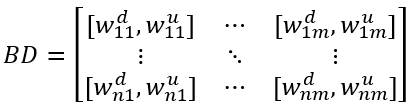
BD是n*m矩阵。w^d_ij是第i个因变量第j个自变量的下边界，w^u_ij是第i个因变量

算法目标

利用X，Y，B，BD在约束条件下拟合出系数矩阵W，生产环境中称为收率矩阵：

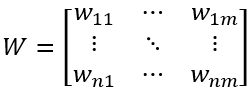
其中W是n*m矩阵。w_ij是第i个因变量（进料）第j个自变量（出料）的收率。

约束条件

1. 所有系数属于[0,1]区间，生产环境中收率不可以小于0或者大于1：

w_ij∈[0,1]

2. 系数矩阵W的各列和为1，生产环境中物料守恒，进料等于出料：

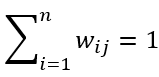
3. 系数矩阵W不可以偏离基础系数矩阵太远，只允许在一个相对较小的范围内取值，生产环境中实际收率只允许在基础收率附近波动。

wb_ij+β₁≤w_ij≤wb_ij+β₂

其中|β₁|，|β₂|相对于wb_ij是一个比较小的数。

算法原理

把自变量矩阵与基础系数矩阵的乘积称为基础因变量矩阵，记为Y’，把因变量矩阵与基础因变量矩阵的差称为误差矩阵，记为E。

Y’=X*B^T

E=Y-Y’

利用有边界的线性拟合算法拟合误差矩阵，得到偏差系数矩阵，记为WE，再通过线性变换将偏差系数矩阵的列和调整为0，将变换后的偏差系数矩阵记为WE’，最后加上基础系数矩阵即可得到系数矩阵W。

Wd^T =linefit_bd(X,E,BD)

Wd’= linetrans(Wd,B)

W=B+Wd’

其中linefit_bd()是由边界的线性拟合函数，BD是允许的边界矩阵；linetrans()是线性变换函数。

如何满足约束条件：

有边界的线性拟合算法将Wd控制在一个较小的范围内，使得最后的系数W不会偏离B太远；基础系数B中的所有系数都在[0,1]之间且列和为1，线性变换时会根据B来变换，将其控制在[0,1]之间，同时使Wd’的列和为0，保证W的所有系数都在[0,1]之间且列和为1；

算法过程

1. 计算误差矩阵E：

E=Y-X*B^T

2. 有边界线性拟合算法拟合偏差系数Wd：

Wd^T=linefit_bd(X,E,BD)

linefit_bd()算法过程参见《有边界的线性拟合算法》。

3. 对Wd线性变换得到Wd’

Wd各列和可能不为0，对其进行线性变化，设Wd是如下矩阵：

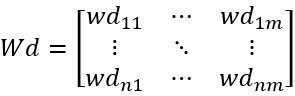
（1） 计算Wd的各列和Wcl：

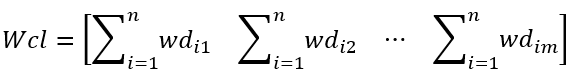
（2） 把Wd每一行看作一个向量，第i行向量为Wd_i

Wd_i=[wd_i1 wd_i2 … wd_im]

偏差系数矩阵可表示成：

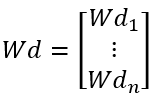
（3） 计算Wd_i以外的其他向量的和组成的矩阵Wds

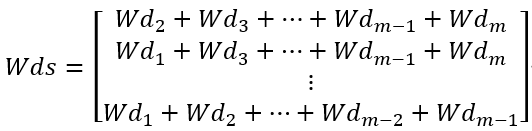
Wds是n*m矩阵，其第i个向量Wds_i=Wd₁+Wd₂+…+Wd_i-1+Wd_i+1+...+Wd_m，是Wd中去掉第i个向量以外的其他向量之和。

（4） 线性变换得到Wd’

Wd_i，Wds_i，Wcl三者有如下关系：

Wd_i+Wds_i=Wcl

已知Wd_i是准确的，则Wds_i=Wcl-Wd_i也是准确的，进行如下线性变换：

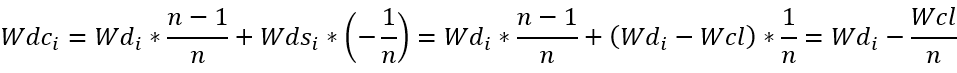
其中Wdc_i=[wdc_i1 wdc_i2 ... wdc_im] 是第i个因变量，m个自变量线性变换后的向量矩阵。

线性变换后，相当于各列的偏差系数减去该列的系数均值。

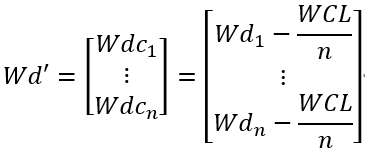
W=Wd’+B

即w_ij=wd’_ij+b_ij。

如果W的各列和符合约束条件w_ij∈[0,1]，则拟合结束，线性变换后的偏差矩阵就是Wd’。

但当存在wd’_ij使得w_ij∉[0,1]时，需要调整变换规则。

假设Wd的第j列Wd_j有z个元素不符合约束条件或者等于0。

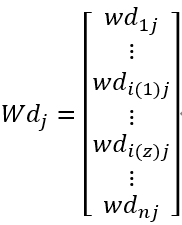
其中wd_i(p)j是第i(p)个因变量，第j个自变量的偏差系数，它不符合约束条件或者等于0，即：

wd_i(p)j+ b_i(p)j∉[0,1] or wd_i(p)j =0

这些元素组成的矩阵是Wdp_j：

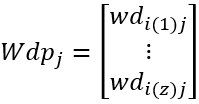
计算Wds_j：

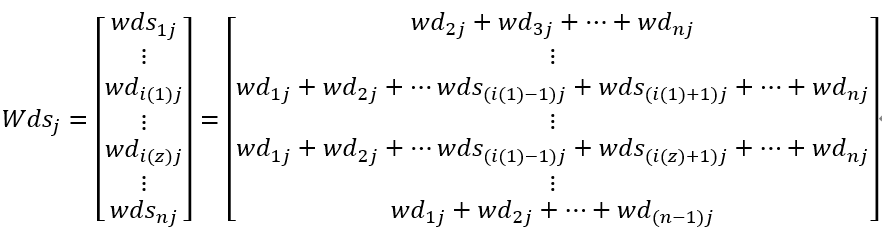
其中wds_ij是第j列第i个元素以外的其他元素的和，即：

wds_ij=wd_1j+wd_2j+…+wd_(i-1)j+wd_(i+1)j+wd_nj

变换方程如下：

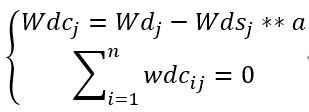
其中Wdc_j是Wdc的第j列元素，a是变换矩阵，是n*1矩阵。

为了使Wdc_j满足约束条件，当wd_ij不满足约束条件时，a_i=0，解上述方程如下：

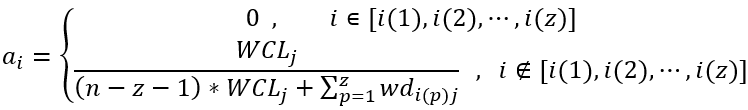
其中z是不符合约束条件或者等于0的偏差系数个数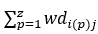，是z个不符合约束条件或者等于0的偏差系数之和，a_i是a的第i个元素。

求得变换矩阵a后，带入Wdc_j=Wd_j-Wds_j**a，求得Wdc_j。

用上述方法求得所有列的Wdc_j，也就得到Wd’。

如果Wd’的所有元素符合约束条件w_ij=(wdc_ij+b_ij)∈[0,1]，则拟合结束，变换后的偏差矩阵就是Wd’。如果仍然有w_ij∉[0,1]，则把对应位置的wdc_ij元素视为不符合约束条件或者等于0的元素，加到Wdp_j中，递归上述方法，直到w_ij=(wdc_ij+wb_ij)∈[0,1]为止，得到Wd’。

变换后的偏差系数Wd’加基础系数矩阵B，得到W

W=B+Wd’

写出代码

输入参数说明：

1. A1中的X是输入自变量矩阵，形状是k*m。

2. A2中的Y是输入自变量矩阵，形状是k*n。

3. A3中的B是输入基础系数矩阵，形状是n*m。

4. A4中的BD是输入边界矩阵，形状是n*m（这里要注意，每一行是1个Y的所有X的边界）。

应用举例

自变量矩阵X：

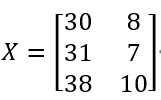
因变量矩阵Y：

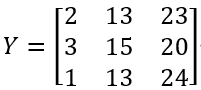
基础系数矩阵B：

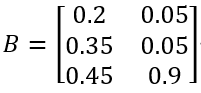
边界矩阵BD：

算法运行结果，最佳系数矩阵W：

最佳系数矩阵W的rmse：

rmse₁=1.64

rmse₂= 2.72

rmse₃= 1.93

rmse_i是第i列Y的rmse。

再来看下最小二乘法直接拟合的结果W：

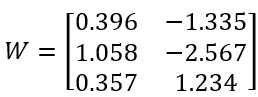
完全不满足约束条件。