有边界的线性拟合算法

已知自变量矩阵X和因变量矩阵Y，两者存在线性关系，但系数被限制在一个范围内，这个范围称为边界，试求出该边界范围内的最佳系数矩阵。

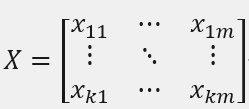
其中X是k*m矩阵，k是样本数，m是自变量数，x_ij是第i个样本的第j个自变量。

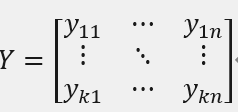
其中Y是k*n矩阵，k是样本数，n是因变量数，y_ij是第i个样本的第j个因变量。

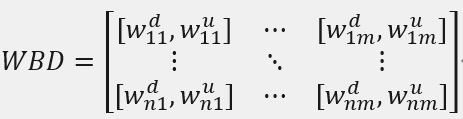
其中WBD的是n*m矩阵。w^d_ij是第i个因变量第j个自变量的下边界，w^u_ij是第i个因变量对应的第j个自变量的上边界， [w^d_ij, w^u_ij]是i个因变量对应的第j个自变量的取值范围。每一行是一个因变量所有的自变量边界。

应用背景

在生产环境中，进料转换成出料的转换率称为收率，收率的取值范围在[0,1]之间，也就是转换率不可以小于0，也不可以大于1。进料矩阵就是自变量X，出料矩阵就是因变量Y，收率的取值范围就是边界矩阵BD。

算法目标：

计算边界范围内的最佳拟合系数。

算法原理：

计算拟合系数通常会使用最小二乘法（LS）来实现，但简单执行LS算法，可能会导致拟合系数超出边界的情况，比如在生产拟合时会出现收率大于1或小于0的情况，这就完全没有意义了。

用最小二乘法求拟合系数的过程本质上是二次函数的极值问题，可以证明，在有界范围，二次函数的极值可能在边界上，也可能在偏导数为0的位置，穷举所有X的系数边界和偏导数为0的所有可能，每个自变量对应的系数都有3种取值，分别是上界，下界，偏导数为0，m个自变量就会有3^m种可能，找到使rmse最小的一套系数即为边界范围内的最佳系数。在m不大的时候，这个算法具有实际可行性。

算法过程：

设求得的系数矩阵W如下：

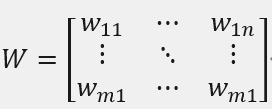
其中W_ij是第i行，第j列的元素。

1. 计算每列因变量的系数

所有可能的系数组合共有3^m种，记为s。

s=3^m

用Y_j表示Y的第j列元素，用X_h表示X的第h列元素。

（1） 若没有自变量取到边界，则所有自变量的系数都是偏导数为0时的系数；

W_j^(r)=linefit(X,Y_j)，r∈[1,s]

其中linefit()函数是最小二乘法拟合得到的系数，W_j ^(r)是Y_j对应的第r个系数矩阵。

（2） 若某些自变量的系数取到边界，其他列的系数需要偏导数为0求得；

假设X_a,X_b,…,X_k这些自变量的系数取到了边界，则这些自变量的系数已经知道，为W_aj,W_bj,…,W_kj。

未取到边界的自变量记为X’，对应的因变量Yj’

Y_j’=Y_j-(X_a*W_aj+ X_b* W_bj+…+X_k* W_kj)

系数矩阵记为W_j’

W_j’=linefit(X’, Y_j’)

将W_aj,W_bj,…,W_kj按序合并后即得到相应的W_j^(r)。

（3） 若所有自变量的系数都取到边界，则这些边界就是一组系数。

经过(1)(2)(3)就得到了s=3^m组系数，即W_j ⁽¹⁾, W_j ⁽²⁾,…, W_j ^(s)。

（4） 筛选所有系数都在边界内的系数W_j ^(r’)

W_j ^(r’)= W_j ^(r), w^d_ji≤W_j ^(r)_i≤w^u_ji

其中W_j ^(r)_i是W_j ^(r)的第i个的元素。

（5） 计算每组系数关于Y_j的rmse^(r’)。

Y_j’=X* W_j ^(r’)，r∈[1,s]

其中Y_j’是X与W_j ^(r’)的预测结果。

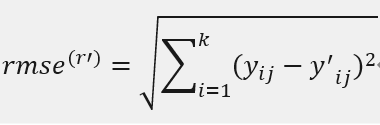
其中y_ij是Y_j的第i个元素是，y’_ij是Y_j’的第i个元素。

（6） 使rmse^(r’)最小的W_j ^(r’)即为最佳系数矩阵W_j

所有的rmse^(r’)组成的序列称为rmse序列，记为RMSE。

W_j=W_j^(r’),rmse^(r’)=min(RMSE)

2. 合并所有因变量的最佳矩阵就得到最佳矩阵W。

写出代码：

输入参数说明：

1. A1中的X是输入自变量矩阵，形状是k*m。

2. A2中的Y是输入自变量矩阵，形状是k*n。

3. A3中的BD是输入边界矩阵矩阵，形状是n*m（这里要注意，每一行是1个Y的所有X的边界）。

应用举例：

自变量矩阵X：

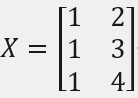
因变量矩阵Y：

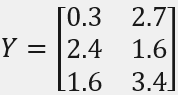
边界矩阵BD：

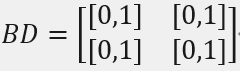
1. 先来看下直接用最小二乘法的拟合结果

系数矩阵W：

系数矩阵W的rmse：

rmse₁= 0.684

rmse₂= 0.684

注意：约束条件是所有收率都不小于0且不大于1，这种方式肯定是无法满足需求的。

2. 再来看有边界的线性拟合算法拟合结果

最佳系数矩阵W：

最佳系数矩阵W的rmse：

rmse₁= 0.697

rmse₂= 0.697

rmse₁是第1列Y的rmse，rmse₂是第2列Y的rmse。

说明：虽然简单最小二乘法的拟合结果更好，但因为有边界约束条件的限制，还是要选择有边界的线性拟合算法。