我们来看一个例子，下图是一组球员的年收入数据，单位万美元，他们的平均收入是多少？

很容易，我们能够计算出他们的平均年收入是 597 万美元，这么看球员似乎是一个非常高薪的职业，但是仔细观察就会发现在 16 个球员中只有 1 号球员和 2 号球员的的收入在平均值以上，而其他 14 位球员的收入均低于平均值。很显然在这组数据中平均值并不能够代表大多人的收入状况，以平均值来描述球员的典型收入是不合理的。

那么，如何来正确描述呢，这就涉及到数据的描述方法。

所有的数据都可以归为两大类定量数据和定性数据。

对于定量数据来说可以从四个维度来描述，即集中趋势测度、分散测度、相对位置测度和对称性测度。

（1）集中趋势测度

如上图中所示，集中趋势测度包含平均值，中位数和众数

平均值是使用频率最高的，计算也非常简单，基本人人都会

中位数是将数据集以升序（或降序）排列后，处于中间的数值，

将 n 个测量值从小到大排列：

如果 n 是奇数，中位数就是中间的数值

如果 n 是偶数，就是中间两个数的平均数

例如：数据集 {3,4,5,7,8} 的中位数是 5，

数据集 {2,4,5,7} 的中位数应当是(4 + 5)/2=4.5

众数是数据集中出现频率最高的数

例如：数据集 {1,2,2,3,4,7,9} 的众数是 2

平均值是最常用、最容易理解的集中趋势测度，如果数据的分布正常，平均值通常是中央趋势的最佳度量。如果数据集中存在几个极大 / 极小值或数据集偏斜，则中位数是中央趋势的最佳度量

例如下列两组数据 test1 和 test2，用易明建模工具 YModel 打开数据，统计结果如下：

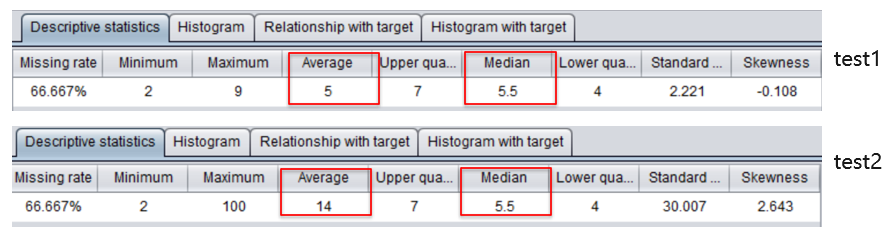
在 test2 中由于极值 100 的存在，平均值受到影响，中位数不变，因此对于 test2 用平均值来描述来描述集中趋势已经严重失真了，应该选用中位数比较合理。

同样我们回到球员收入的例子，1 号球员和 2 号球员年薪要远远高于其他球员（可能是明星球员），对平均值产生了较大影响，而中位数 172 会比较准确的描述球员的典型收入状况。

（2）分散测度

集中趋势的测度仅仅提供了数据集的一部分描述，这种描述是不完全的，数据有许多其他方面的显著差异不能用集中趋势来描述，例如下图两组数据，X1 和 X2 的平均值和中位数都相同，但数据的分散测度却不相同。

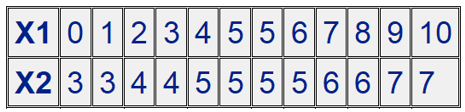
数据集的分散测度（也称变异性），表示数据的散布或分散程度，数据的变异性同样也很重要。分散测度包括极差、方差和标准差。

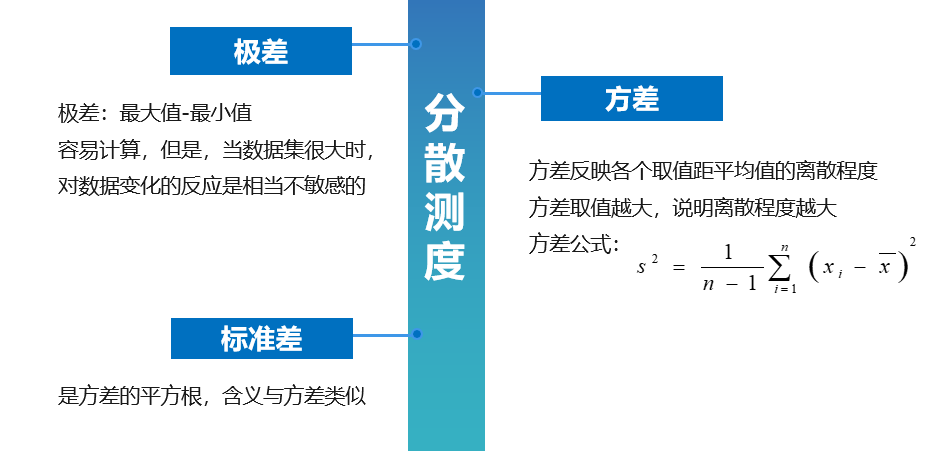
极差比较容易计算，但是，当数据集很大时，对数据变化的反应是相当不敏感的，不常用

例如下面两组客户的年龄数据，用易明建模 YModel 工具统计得出两者的极差是相同的，但是数据特点并不相同，Age1 表示主要客户群体是青年人，Age2 表示主要客户群体是中老年人

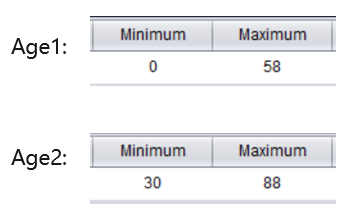
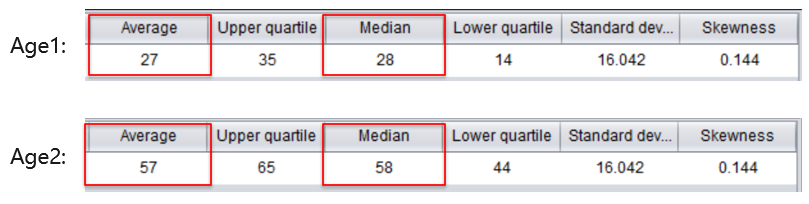
方差和标准差是比较常用的两个指标，反映各个取值距平均值的离散程度，取值越大，说明离散程度越大

比如两组同学的数学成绩如下：

第一组：50，100，100，60，50

第二组：73， 70，75，72，70

不难计算出两组成绩的平均值相同，但标准差不同，离散性不同

第二组的成绩更加稳定

（3）相对位置测度

相对位置的测度，描述一个测量值相对于其他数据的关系的测度：上四分位数、下四分位数，z-score

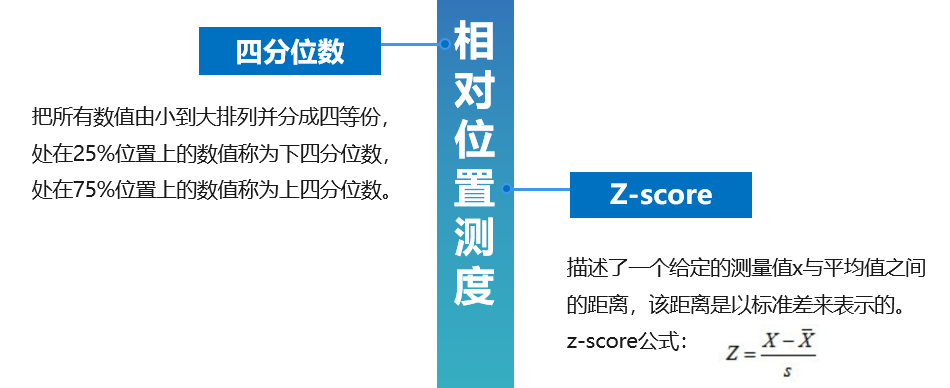
四分位数通常用箱线图表示

箱线图和 z-score 是进行异常值判断的重要指标

（4）对称性测度

除此之外对称性测度也是非常重要的测量维度，在数据挖掘中，偏度是一个很重要的指标

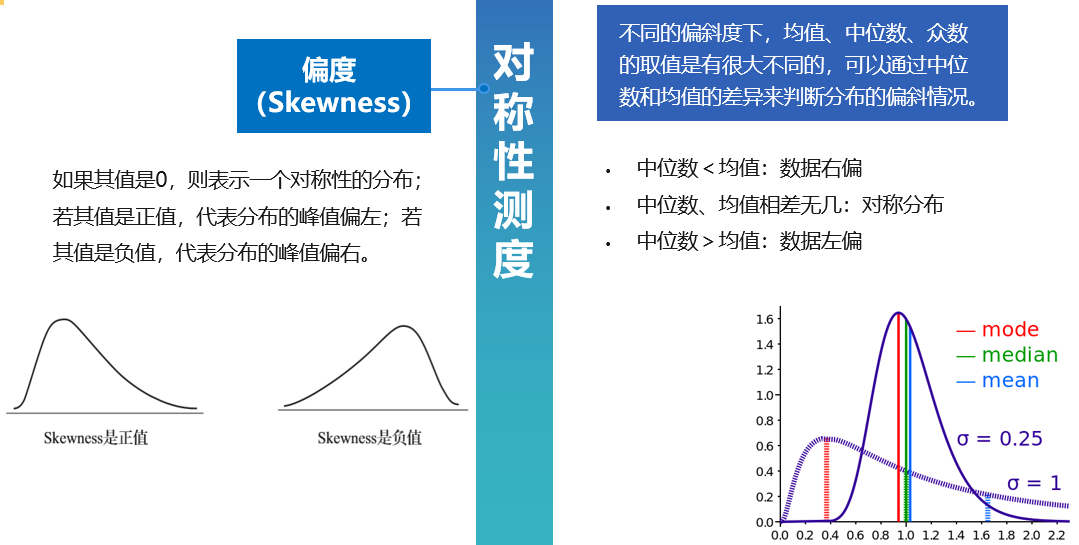
偏度的绝对值如果大于 1 是个很明显的信号，说明你的数据分布有明显的不对称性。很多数据分析的算法都是基于数据的分布是类似于正态分布的钟型分布，并且数据都是在均值的周围分布。如果偏度的绝对值过大，则要小心地使用那些算法！

例如球员的收入数据 Skewness=2.291，中位数 < 平均值，数据右偏，这样的数据往往是不能直接拿来建模的，需要经过预处理才能使用。