【程序设计】6.1 [重复用] 自定义函数
6.1 自定义函数
还是假定没有阶乘函数，现在想计算组合数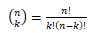
。
A |
B |
C |
|
1 |
10 |
4 |
|
2 |
=1 |
for A1 |
>A2=A2*B2 |
3 |
=1 |
for B1 |
>A3=A3*B3 |
4 |
=1 |
for A1-B1 |
>A4=A4*B4 |
5 |
=A2\A3\A4 |
n 和 k 分别填入 A1 和 B1，第 2、3、4 行分别计算出 n!，k! 和 (n-k)!。
这个计算没问题，但是，几乎同样的代码写了三遍。
如果问题再麻烦一点，比如我们要计算二项式定理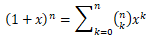
中的系数序列（也就是帕斯卡三角的某一行）。循环函数可以一句算出多个值，但必须在表达式中容易写出来的才可以，还需要几行代码才能实现 的计算，就还得用循环语句来做了：
A |
B |
C |
D |
|
1 |
10 |
=1 |
for A1 |
>B1=B1*C1 |
2 |
for A1-1 |
=1 |
for A2 |
>B2=B2*C2 |
3 |
=1 |
for A1-A2 |
>B3=B3*C3 |
|
4 |
=@|(B1\B2\B3) |
|||
5 |
=1|B4|1 |
其实，包括 SPL 在内的大多数程序语言都允许我们把要重复执行的代码写成自定义函数，然后就可以反复调用了。
A |
B |
C |
D |
|
1 |
func factorial(n) |
=1 |
for n |
>B1=B1*C1 |
2 |
return B1 |
|||
3 |
=factorial(10) |
=factorial(4) |
=factorial(6) |
=A3\B3\C3 |
A1 格的 func 语句定义了一个名字为 factorial 的函数，它的代码就是 A1 的代码块，其中 n 是函数的参数，可以在代码块中使用。SPL 碰到 func 格子，会先跳过这个代码块往后看去执行后续的代码。
SPL 会将自定义的函数自动登记起来，然后就可以像普通函数一样使用了。比如 A3 格中用这个函数计算了 10 的阶乘。SPL 会把函数参数填进相应的变量（这里就是 n)，然后让程序跳转到函数的代码块（也就是 A1）去执行，即开始执行 B1:D2。
B1:D1 的代码我们已经能理解了，它能够计算出 n 的阶乘并填入 B1。当 n=10 时，这段代码就计算出 10! 并填入 B1。然后 B2 格的 return 语句将 B1 的值返回，这时候程序又会跳回到调用这个函数的地方，即 A3，并得到了 factorial(10) 的返回值 10！，A3 的格值就是 10！。
也就是说 A1 代码块的自定义函数 factorial 将计算出其参数的阶乘值返回。
同理，B3 将计算出 4!，C3 将计算出 6!，最后在 D3 计算出组合数 。
整个过程看起来还是有点复杂，但无论如何，这 3 个阶乘数使用了同一段代码计算，不需要把代码写三遍了。
总结一下：用 func 语句定义函数，其中要有 return 语句返回计算结果。然后使用定义的函数名来传入参数调用这个函数。
自定义函数也是个函数，它和 SPL 自有函数的地位是等同的，可以放在表达式里参与计算。
A |
B |
C |
D |
|
1 |
func factorial(n) |
=1 |
for n |
>B1=B1*C1 |
2 |
return B1 |
|||
3 |
=factorial(10)\factorial(4)\factorial(6) |
|||
这样也能正确计算出结果。
而且，自定义函数也可以用到循环函数里。
A |
B |
C |
D |
|
1 |
func factorial(n) |
=1 |
for n |
>B1=B1*C1 |
2 |
return B1 |
|||
3 |
10 |
=factorial(A3) |
||
4 |
=1|(A3-1).(B3\factorial(~)\factorial(A3-~))|1 |
|||
二项式的系数计算也看着更清晰了。
我们再举一个有点实际用途的例子：在一批平面上的点中找出异常点。办法是这样：计算每个点到其它点的距离之和，然后从大到小排序，前 10% 的点就认为是异常点，因为它们距离其它点相对比较远，可以认为是异常点。
A |
B |
C |
|
1 |
100 |
>X=A1.(rand()) |
>Y=A1.(rand()) |
2 |
=to(A1) |
=A2.(A1.sum( distance(X(A2.~),X(~),Y(A2.~),Y(~)) )) |
|
3 |
=B2.psort@z().to(int(A1*0.1)) |
||
4 |
|||
5 |
func distance(x1,x2,y1,y2) |
||
6 |
return sqrt((x1-x2)*(x1-x2)+(y1-y2)*(y1-y2)) |
||
在 A5 定义一个函数 distance 用来计算两个点的距离，它有四个参数，分别是两个点的横坐标和纵坐标，使用勾股定理可以计算出两点的距离并返回。当自定义函数有多个参数时，分别定义成不同名字就可以了。
函数定义在任何地方都可以，在主程序的前面和后面都不会影响代码的执行。
主程序中先随机生成 100 个点的横坐标和纵坐标。然后在 B2 格就可以调用自定义函数 distance 来计算距离之和了，这是个两层循环函数，内层计算 100 个距离求和（自己和自己的距离为 0，多加一个不会出错，不必把自己排除掉），外层则循环这 100 个点。注意里面的 A2.~ 和 ~ 的差别。
然后用 psort 排序取出前 10% 的点的序号就可以了。
