【程序设计】4.3 [排成队] 多层序列
4.3 多层序列
序列的成员还可以是序列,这样可以构成多层的序列。比如 [[1,2,3],[2,3,1],[3,1,2]] 就是个合法的序列,其每个成员又是一个序列。
我们来看多层序列的成员如何引用:
A |
|
1 |
=[[1,2,3],[4,5,6],[7,8,9,10]] |
2 |
=A1(2) |
3 |
=A1(3)(2) |
4 |
>A1(1)(3)=0 |
5 |
=A1.len() |
6 |
=A1(3).len() |
7 |
>A1(2)=0 |
尝试执行上面的代码,观察运行结果来理解多层序列的成员引用和赋值的动作。
A2 的结果是序列 [4,5,6];A3 取出第 3 个成员序列的第 2 成员,即 8;A4 执行后将使第 1 个成员序列的第 3 个成员变成 0,原来是 3;A5 是序列长度为 3,A6 是第 3 个成员序列的长度,为 4;A7 执行后会将第 2 个成员序列变成 0,这个成员就不再是序列了。
在界面上也可以显示多层序列,上述代码执行完之后,点中 A1 可以在右边看到其值。
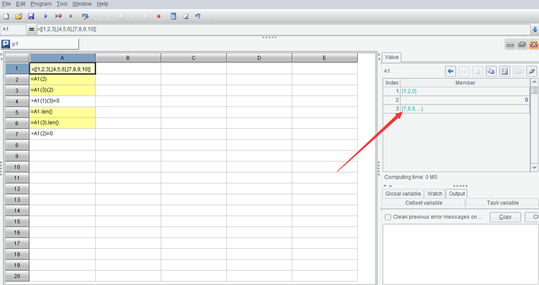
其序列成员也将显示成序列,这时候双击某个序列成员(比如箭头指向的第 3 个成员),将会再显示这个成员序列的成员:
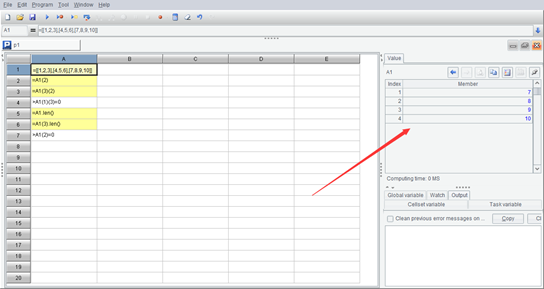
由 n 个长度为 m 的序列构成的序列可以理解成一种二维结构,将每个成员序列写成一行,可以看成是个 n 行 m 列的表格。因此,有些程序语言也把两层的序列称为二维数组,甚至做了特殊处理,可以支持形如 x(i,j) 的写法用于访问第 i 行第 j 列的成员。在 SPL 中没有特殊理解,就是简单理解成第 i 个成员序列的第 j 个成员,即写成 x(i)(j) 的样子。
显然,这些层级还可以更多,对应到数组的术语也就是维度还可以更多。
我们用二层序列来计算帕斯卡三角形(我国称为杨辉三角):
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
……
帕斯卡三角是由 n 行数字构成,第 n 行有 n 个数,第 n 行的第 m 个数是由第 n-1 行的第 m-1 个和第 m 个数相加而成。帕斯卡三角的第 n 行数,恰好是 (1+x)n中 xi项的系数,即:
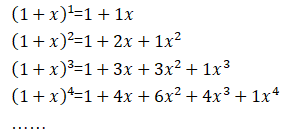
代码很简单:
A |
B |
C |
D |
|
1 |
5 |
=[0]*(A1+1) |
>B1(1)=[1] |
>B1(2)=[1,1] |
2 |
for 3,A1+1 |
>B1(A2)=[1]*A2 |
||
3 |
for 2,A2-1 |
>B1(A2)(B3)=B1(A2-1)(B3-1)+B1(A2-1)(B3) |
||
计算到第 A1+1 行,结果是个二级序列,存在 B1 中。
B1 产生长为 A1+1 的序列准备填入,C1、D1 先填入前两行。A2 的循环从第 3 行起计算,B2 产生一个长度为 A2 的全 1 序列用于当前行,然后从第 2 列计算到第 A2-1 列,因为这一行的第 1 列和第 A2 列都是 1,不必计算了。



