2.2 分支结构

用 if() 函数可以完成一些判断，但有些情况，我们还需要 if 语句。

回顾一下中学学过的二次方程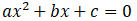，可以用公式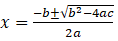解出方程，但是要考察其中那个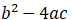，如果它大于 0，则有两个解，如果它等于 0，则只有一个解，如果它小于 0，则没有实数解。

我们来编段程序求解这个方程，假定系数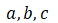已被填入单元格 A1,B1,C1 中，要求把求出的解写到 A2 和 B2 格中。如果有两个解则把 A2 和 B2 都填上；如果只有一个解则只填 A2；没有解则都不填。

B4 和 C4 的 sqrt() 是平方根函数，这不必详细解释。重点在于 A4 和 A5 出现了 if 语句。

在 if 后面跟一个逻辑表达式。如果这个表达式计算结果为 true，程序会继续执行 if 所在格右边的格子；如果计算结果为 false，程序将跳过 if 所在格右边那些格，直接走到下一行执行。

注意，这个 if 并不是上一节说的 if() 函数，它后面可以没有括号（有也可以，括号会被当成逻辑表达式的一部分，在表达式外套一层括号不会改变表达式的计算结果），而且一定要写到格中代码的开头。

这是 if 语句最简单的形式：条件成立则向右执行，否则直接向下。

这段代码没有错误，但是有个小毛病。在 A4 格判断 A3 大于 0，如果成立，则将继续执行 B4 和 C4。然后呢？程序还是会执行到 A5，将再次判断 A3 是否等于 0，但这是没有必要的动作了，浪费时间，只有 A3 大于 0 不成立时才有必要再去判断 A3 是否等于 0。

如何避免这个多余的动作呢？代码可以写成这样：

A4 格的 if 和 A5 格的 else 配成了一对，如果 A4 中的判断成立，那么就会执行 A4 右边的格子。如果不成立呢，程序会看 A4 下面是不是有个 else，如果有的话，就执行这个 else 右边的格子。

else 是“否则”的意思，也就是前面的 if 不成立时则执行的动作。

这段程序用了二次方程的求解公式，但前提是方程真地是二次的，也就是说假定了 A1 不是 0。如果 A1 为 0，上面这段程序的 B4、C4 和 C5 格都会发生除以 0 的错误了。我们再继续完善这个代码能处理 A1 是 0 的情况，也就是方程退化成一次方程了。

观察这段代码，很明显，B4:D6 这一段是之前 A3:C5 那一段移过来的，也就是这里 A3 中判断不成立后将要执行的 else 处理。但是，B4:D6 占了三行，并不只是 A4（else 所在格）右边的格子。

这时候，我们要引入 SPL 的代码块概念。

任何一个单元格，如果它的下面及下面的左边都是空的，那么它的右边和右边下面格子构成的块状区域称为它的代码块。比如 A4，它下面的 A5、A6 都是空的，那么从 B4 到 D6 的块状区域称为 A4 的代码块。而对于 A3，它下面的 A4 不是空的，那么它的代码块只有 B3:D3 这部分，不能延伸到第 4 行（A4 不空）。也就是说一个单元格的右边所有格子一定属于它的代码块，但右边格子的下一行是否属于代码块，要看这个单元格下面格子及其左边的格子是不是空。

用文字描述起来比较绕口，但其实从网格布局上看还是很直观的，看下面的网格：

B1 的代码块是 C1:D1，因为 B2 不空；

B2 的代码块是 C2:D3，因为 A3:B3 空，而 B4 不空；

C3 的代码块是 D3:D3，因为 B4 不空；

A5 的代码块是 B5:D6，因为 A6 空。

代码块是为了限定语句的作用范围。if 的条件成立，则执行 if 所在格的代码块；不成立，则执行对应的 else 所在格的代码块。

有些程序语言会使用花括号或者 BEGIN…END 来把要执行的语句括起来，使用这种方案的程序语言，对书写格式没有要求。但人们为了易读，仍然会使用文本缩进把代码写成这种阶梯状以看清每条语句的作用范围。SPL 没有采用括号方案，直接使用阶梯状的代码块来限定语句作用范围，这将强制代码有一定的格式。

上面的代码也可以把 A3 的条件反过来写，平方根计算也可以只做一次：

A3 的代码块是 B3:D6，在 A3 的判断条件成立时将被执行，否则将执行对应的 else 所在格 A7 的代码块 B7:D7。

我们还要进一步考虑方程退化的情况，即 A1 和 B1 都是 0 的情况，这时候，如果 C1 也是 0，那么任何数都是这个方程的解，如果 C1 不是 0，那么这个方程无解。

当方程退化为 0=0 时，代码不填入任何解，并在会右下输出一个 Any。

像上面代码中，else 的代码块中还有 if，这种情况在现实有并不少见，这会导致整个代码很宽，因为每多一层 if 就需要向右边缩进一层，代码的美观度和易读性都不太好。

包括 SPL 在内的许多程序语言都提供了把 else 和其后 if 绑定的语法，上面这段代码还可以写成这样：

把紧跟着 else 的 if 和 else 写在一起, 这些 else if 和第一个 if 构成一条完整的 if 语句。相当于一批互斥条件分别判断，某个条件成立则执行相应的代码块，然后结束整个 if 语句。

【程序设计】 前言及目录
【程序设计】2.1 [做判断] 逻辑运算
【程序设计】2.3 [做判断] 注释和跳转