1.1 数据

运行集算器，点击新建（菜单命令：文件 - 新建），可以看到这么一个网格式的界面：

SPL 代码就是写在这个网格里，看起来有点像 Excel，但其实不是。

大多数程序语言的代码都是写成一段文本，如果没有被特别代码改变次序的话，一般会从前向后执行。SPL 略不一样，写到了网格中，每个格子里都可以写入代码，执行次序也是从前向后的，具体来说是一格一格执行，每一行从左到右执行每个格子，然后再执行下一行的格子。本质上和写成文本并没有多大区分，不过我们会在后面看到这种网格式的代码对于非专业人员比文本式的代码要更为友好。

大多数程序设计书的第一个例子都是写一个能输出一句“Hello,World”的程序，这其实是早期命令行时代留下来的后遗症，当代操作系统都是图形界面了，再做这么个事反而麻烦，我们就跳过这一步。

作为计算机程序，显然要会做计算器上能做的事。我们来试试，在网格写入代码：

注意，每个格子里的第一个等号是必须写的（先不管为什么），代码中的括号必须用英文的括号，使用中文括号会报错（可以试试看看报出什么样的错误）。

现在，按 Ctrl-F9 执行程序，格子的底色变成了黄色。然后，点击每个黄色格子，都可以在右边看到这个格子计算出来的值：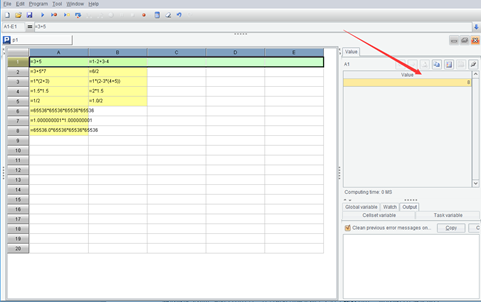

在执行之前，格子是白底的。这时即使写好了公式，点击格子，右边出现的也是空值，它并不会像 Excel 那样自动计算。计算机程序通常都需要有个执行动作，而不会自作主张地自动做事情。

我们来观察这些计算结果：

这些计算式写起来和我们平常书写的差不多，乘法要写成 *，除法要写成 /，计算次序也是先乘除后加减，这些和 Excel 公式的规则一样；

无论多少层括号，都只有圆括号，没有方括号和花括号，如果括号不匹配，那就会出现计算错误，这也和 Excel 一样；

正数负数都能计算，小数和整数都能计算，还是和 Excel 一样。

再仔细观察，A1/B1/A2 的计算结果都是整数，没有显示小数点。但 B2 和 B4 的计算结果明明也是整数，为什么会显示成 3.0，多了小数点呢？

原来，在计算机中，有小数点的数和整数被认为是两种不同的数，有小数点的数被称为浮点数，没有小数点的数仍然叫整数。

我们平时做算术时并不关心整数还是浮点数，反正算出来是什么就是什么。但用计算机编程时，首先要确定你要计算的数是整数还是浮点数，因为在计算机中，整数和浮点数的存储方式是不同的，计算手段也是不同的，如果搞错了，那结果也可能是错的。编程时，搞清数据类型是非常基础和重要的事情。

为什么要把整数和浮点数分开呢？整数可以看成小数部分为 0 的浮点数，那么只用浮点数不就行了？

从数学上讲，这没有问题。但计算机要实际执行这些运算，就要考虑一些工程问题。浮点数的存储和计算都比较麻烦，整数的存储和运算要简单得多，如果把整数都当成浮点数来处理，那整数的运算效率就只能和浮点数一样差了，但有时候要执行的大部分运算都只涉及整数，如果按浮点数来运算就划不来了。而计算机并不知道这一点，所以要请程序员自己分清楚。

大多数程序语言中都会把整数和浮点数分开，但大都允许它们写在同一个表达式中，这时候就会先把整数转换成浮点数再计算（整数总是可以转成浮点数，但反过来不一定）。除法很可能会计算出浮点数，所以 SPL 约定除法结果总是一个浮点数，以保证这个运算结果的数据类型的确定性，否则你可能就搞不清这一步会算出来什么。在 SPL 中，还提供了一定返回整数的除法，用反斜杠 \ 表示，你可以试试 =6\3 会计算出什么，再试试 =5\3。

再观察 A6，它竟然算出来 0，这是怎么回事？！

计算机的存储是有限的，而表示一个大数需要更多的存储空间，计算机不可能表示无限大的数，所以要对数据的大小做出限制。大部分当代程序设计语言中的整数有两种：32 位和 64 位的，这个 32 和 64 是指二进制数的 32 位数和 64 位数（不明白什么是二进制的读者请自己搜索，这里不费篇幅了），这样，最大也就只能表示 2^32­和 2⁶⁴这么大的数（事实上还要小一半，是 2^31­和 2⁶³，因为还要用一位去表示负数）。如果计算结果超出这个范围，就会发生错误了。

SPL 在整数计算时也最多只能用到 64 位数，4 个 65536 相乘超出了这个范围，所以得到了错误结果。而且，不幸的是，几乎所有程序设计语言都不会报这个错，就由它算出错数，SPL 也遵循了这个惯例，这种可能的错误只能编程者自己注意了。

为什么要造 32 位和 64 位两种整数？理由和前面差不多，大部分运算用 32 位的数就够了，而 64 位数占用空间和计算效率都差一点，没必要的时候就别用了。而再短的 16 位数就常常不够大了，再多造一种数又太麻烦了（其实早期计算机确时有 16 位数，甚至还有 8 位的，有意思的是这些位数都是 2ⁿ，没有 18 位、25 位这种位数）。

SPL 把 32 位数还是叫整数，64 位数被特别称呼为长整数，当代的其它程序语言也大都也是这么约定的（早期的不一定）。

不过，不管是 2³¹还是 2⁶³都是很大的数了，通常我们用不到这么大的数，大多数情况也不必在意它。

再看 A7，它的计算结果看起来也不是期望值，这又是啥情况？

和整数的有限性类似，浮点数的存储空间也是有限的，它的有限性不仅表现在数值本身有限（大概是±10³⁰⁸），更重要的表现在于精度，它只有大概 18 位有效数字，再多就只能舍弃了，也就出现的 A7 这种情况。

而且，注意还有而且。我们知道，现代计算机都是用二进制来计算的，十进制的整数写成二进制是精确的，但十进制的有限小数写成二进制很可能是个无限循环小数（道理自己去脑补）而无法被计算机精确表示，比如 0.1 就不行。这样的数如果反复多次运算，可能产生积累误差，出现不可预料的错误。

整数是精确的，反复运算也不会错。所以，能用整数时就别用浮点数。

再看 A8，与 A6 不同，我们把一个 65536 写成 65536.0，就表示告诉计算机，这个 65536 是个浮点数而不是整数，SPL 在计算时会把其它数先转换成浮点数，而浮点数的界限要比整数大得多，这样就不会越界，也就能计算出结果了。

但计算出来的 1.8446744073709552E19 又是个什么？

这叫计算机的科学计数法，它就表示 1.8446744073709552*10¹⁹，这也是所有程序语言的惯例写法，在代码中也可以书写 1.23E-20，就表示 1.23*10^-20。

SPL 中除了整数、长整数和浮点数，通常还有大数（可以表示任何长度和精度的数，但运算更慢）、字符串、日期时间等其它数据类型，这些我们会在后面讲到。

学习一门程序语言，首先要关注它提供的基本数据类型。

【程序设计】 前言及目录

【程序设计】1.2 [做算术] 变量和语句