大佬们，周末好😄

请问集算器对序列操作的时间复杂度是什么样的，比如：

1、在序列头部位置删除一个元素，A.delete@n(1) 的时间复杂度是 O(n)?

2、在序列头部位置插入一个元素，A.insert(1,[val]) 的时间复杂度是 O(n)?

3、在序列尾部位置删除一个元素，A.delete@n(-1) 的时间复杂度是 O(1)?

4、在序列尾部位置插入一个元素，A.insert(0,[val]) 的时间复杂度是 O(1)?

以上描述是我臆测的，我看到一些资料说常规序列对头部位置的操作是 O(n)，因为涉及到后续元素位置的改变，而对尾部位置的操作是 O(1)，因为不涉及前面元素位置的改变，直接利用分配好的位置就行。不知道集算器是用什么数据结构实现序列的操作的，如果是用双端队列实现的那是不是全是 O(1) 的时间复杂度？

为什么会有这样的求助？实践中经常会碰到一些深搜，比如以下 BOM 展开的例子，如果用递归解决，代码简洁，但递归很容易堆栈溢出，所以换成了迭代深搜，用序列来模拟栈，此时就涉及到了对序列操作的问题，是操作头部好还是操作尾部更好。如下所示，需要根据需求表中出货产品和数量按照 BOM 表中的父子结构求出最终材料的总数量并描述出材料路径：

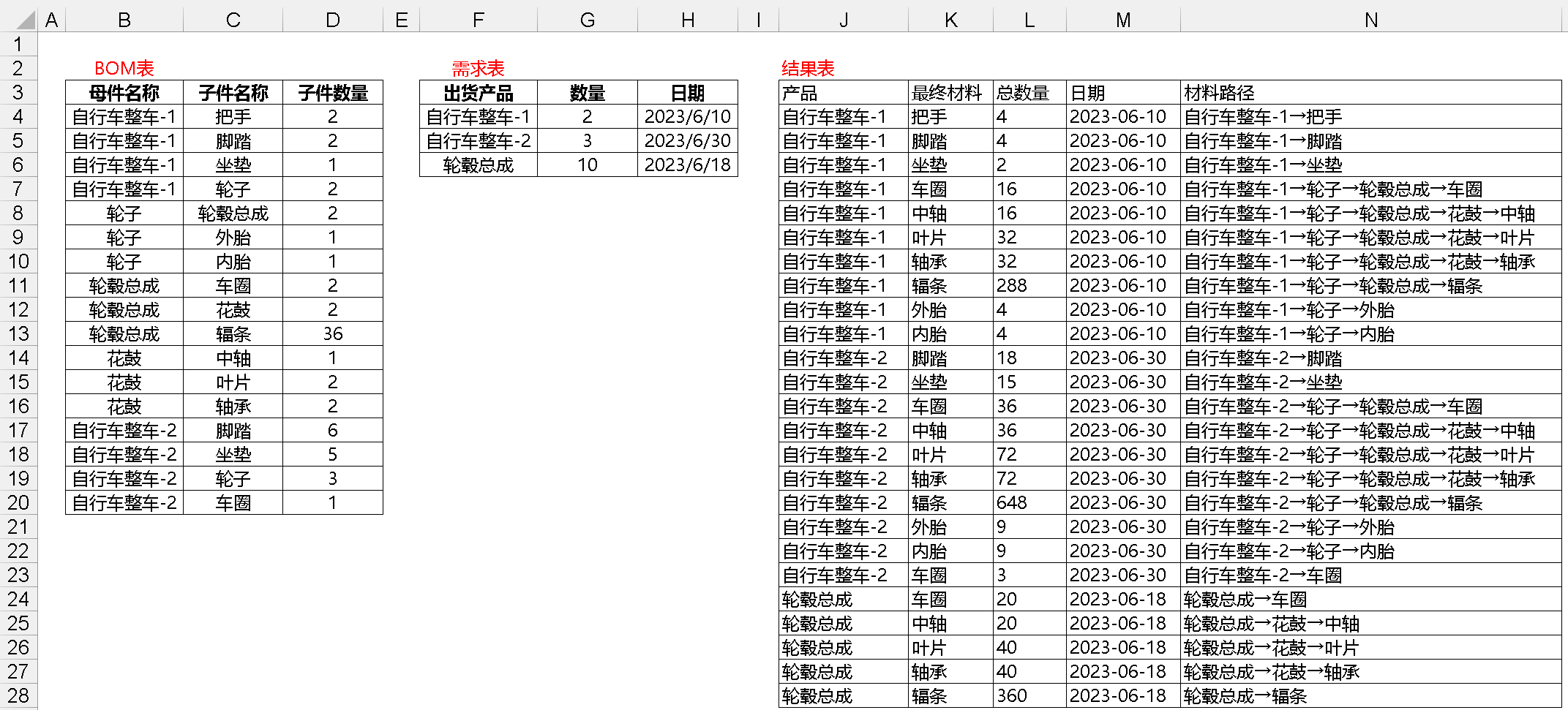
递归写法如下，很直观简洁，但效率一般：

然后改成了迭代深搜，这个效率比递归的效率要高：

迭代深搜相当于是后进先出了，所以用序列模拟栈时，不管是出栈还是入栈，都从序列的尾部操作，但为了跟递归结果保持同序，图中的子件集要反转一下。

但又有资料说可以广度优先，也就是先进先出，那就要操作队列的头部，以下写法结果是对的，但不一定是广度优先，这有点懵。出栈时从头部位置出栈，但入栈还是从尾部入栈。

上述两种方法殊途同归，我想请教的是，类似这种出栈入栈的操作，集算器在最佳实践上是不是要保持同方向，也就是说：

1、出栈时在头部位置，那入栈是不是也要操作头部位置；出栈时在尾部位置，那入栈也应该在尾部位置。不能交叉，一个操作头部另一个操作尾部。之前好像碰到一个问题，因为操作方向不一样，程序没跑出来，但又找不到那个例子，无法复现。

2、又回到了一开始的问题，是操作尾部位置好还是操作头部位置好，哪一个时间复杂度更低，或者两者都一样都是 O(1)?

3、还有一个一直想问的问题，我写的递归，同样的逻辑，在集算器里跑会比在其他程序里跑略慢，像本文中一开始提到的递归写法，是不是函数式编程递归写法？这样写效率还好一些，如果改成那种回溯写法，就是要恢复原始现场的写法，运行效率会慢一些，这个也一直存在困惑，大佬们可否顺便指导一下如何在集算器里写出高效递归？是不是在能不用递归的场景下尽量不用递归。

恳请大佬们得闲时给予指导解惑，谢谢🙏