工业 AI 监盘发现异常实践
背景与任务
在工业生产场景中,成百上千个测量仪表7×24小时不间断运行,产生海量数据。这些随时间而产生的数据称为时序数据。时序数据是设备运行状态的“晴雨表”,如果能及时发现异常,就能将设备故障控制在萌芽阶段,避免重大生产事故发生。
所以我们的任务就是及时发现时序数据中的异常。
及时要求时效性高,最好是采集到数据的第一时间就能判断该数据是否异常,比如下图中的第86个点,刚采集到就给出了实时报警。
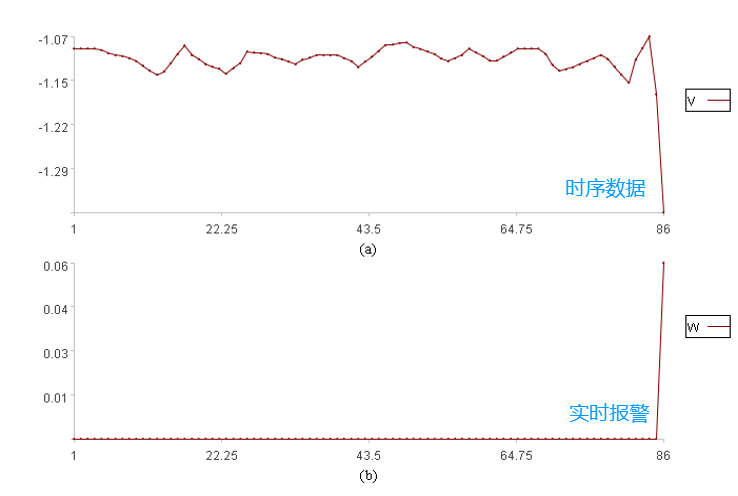
除了时效性,还要求能发现不同类型的异常,下图是部分常见异常举例:
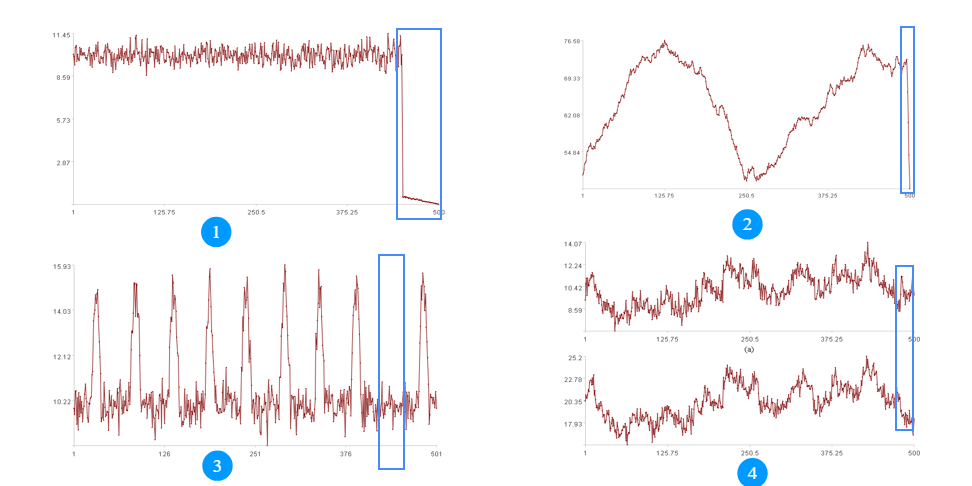
其中①是值越界,②是变化越界,③是周期缺失,④是二维数据反向变化。
算法设计
工业设备数量庞大,完全依赖人工监控既不现实也不可靠,因此我们需要一种能够自动发现异常的高效方法。
传统的机器学习方法通常依赖大量已标记的异常数据,然而在真实工业场景中,数据规模巨大,人工标注不仅成本高昂,标记质量也难以保证。
当前AI大模型受到广泛关注,容易想到采用大模型来实现异常发现。经过简单测试,预训练的大模型确实具备一定的异常发现能力,但结合到实际应用场景,仍存在很多明显的局限:
1. 大模型大多基于自然语言处理任务训练,并未专门针对异常发现场景进行优化,用于异常发现容易产生较高的“幻觉”,表现极不稳定,误判频发;
2. 提升大模型在异常发现上的准确率,通常需要对其进行微调,这将带来高昂的开发成本,包括大量标注数据、算力资源等,对工程师团队要求也非常高;
3. 大模型推理过程的资源消耗虽然远低于训练,但仍然开销很大,无法适应生产环境的低成本要求。而且运算性能不足,难以实时应对较大规模和较高频率的采样数据。
在综合权衡后,我们选择了自研的无监督学习的数学算法来完成异常检测任务。然而,在缺乏标注数据的情况下,如何定义“异常”呢?
我们的基本思路是:正常运行的生产设备,大部分情况是正常的,发生异常是罕见情况。因此可以这样定义:异常是历史数据中没发生或者少发生的情况。
举个容易理解的例子:A同学平时考60分,有一天突然考了90分,大家一定认为该同学的分数异常了。
之所以认为90分异常是因为历史数据中90分发生的概率低甚至没发生过。如果A同学不断努力,成绩稳步提高65,70,75,80,85,经过一段时间,该同学再考90分的概率就大大提高,异常程度就没那么高甚至可以认为是正常了。
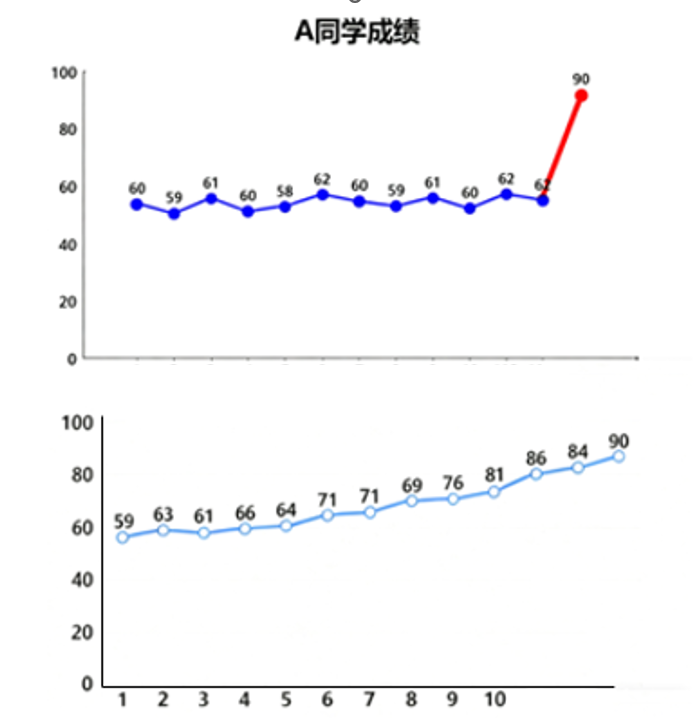
当然,工业场景下情况复杂得多,经常并不能只用简单值(比如成绩)就能发现所有异常,还会用到变化快慢、离散程度等复杂的数学量。
数学方法描述异常过程如下图:
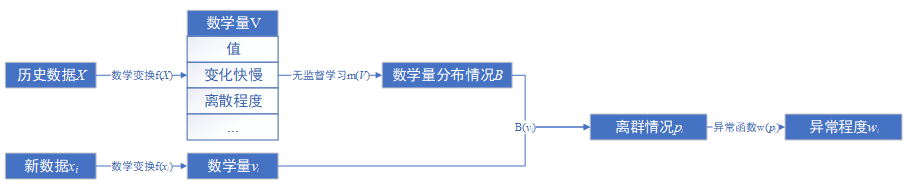
寻找某个数学量,并用历史数据计算该数学量的分布,新数据相对于历史分布的离群程度,就可以用来表征异常程度。
计算数据分布的方法有很多,比较朴素的方法是用历史数据计算出一个范围,把大多数数据框在该范围内,对于新来数据,如果超出该范围,则异常。
比如90分是新数据,异常程度计算过程如下:
时序数据:X=[60,59,61,60,…,62]
数学量:V=X
数据范围:td,tu=box(V)=58,62
新数据:xn+1=90
新数学量:vn+1=xn+1=90
异常程度:pn+1=max(vn+1-tu,td-vn+1,0)/(tu-td)=(90-62)/(62-58)=7
除此之外,发现异常的方法还有概率密度法:
概率分布:g(…)=dense(V)
异常程度:pn+1=g(vn+1,l,h)/θ-1
典型场景
值越界
数据走势图:
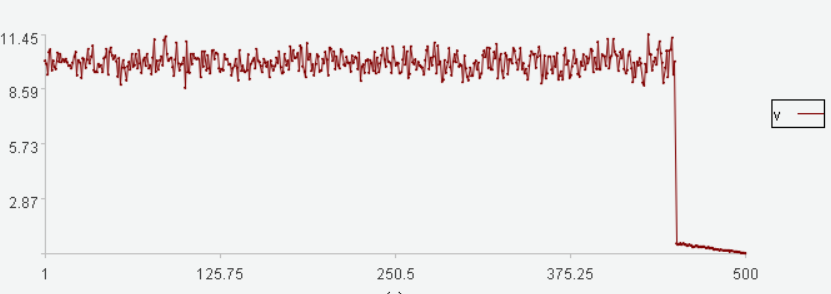
横坐标是数据序号,纵坐标是数据取值。
最后一段数据值过小,相较于之前数据没出现过,应该被识别为异常。
示例代码:
A |
B |
C |
||
1 |
value.json |
|||
2 |
=json(file(A1).read()) |
/read data |
||
3 |
500 |
/learn_interval |
||
4 |
dense |
/method |
||
5 |
=A2.to(500) |
/learndata |
||
6 |
=A2.to(501,) |
/predictdata |
||
7 |
=[] |
|||
8 |
=[] |
|||
9 |
=[] |
|||
10 |
for A6 |
=A5.insert(0,A10).delete(1) |
||
11 |
if A4=="box" |
=box(B10,A10,3) |
/tu,td,p |
|
12 |
=A7.insert(0,C11(1)) |
|||
13 |
=A8.insert(0,C11(2)) |
|||
14 |
=A9.insert(0,C11(3)) |
|||
15 |
else if A4=="dense" |
=dense(B10.([~]),[A10],[[0,100]],[2],1) |
/dense,p |
|
16 |
=A9.insert(0,C15) |
|||
17 |
=A9 |
|||
范围分布报警结果图:
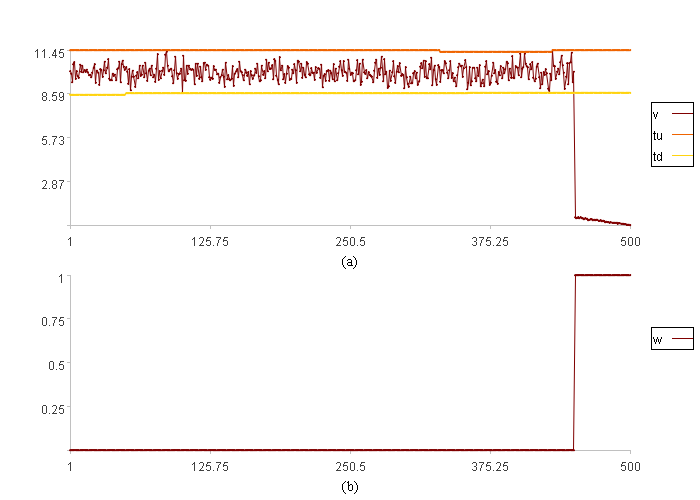
图(a)中v是数据取值,tu是范围上限,td是范围下限。
图(b)中w是数据异常程度。
概率密度分布报警图:
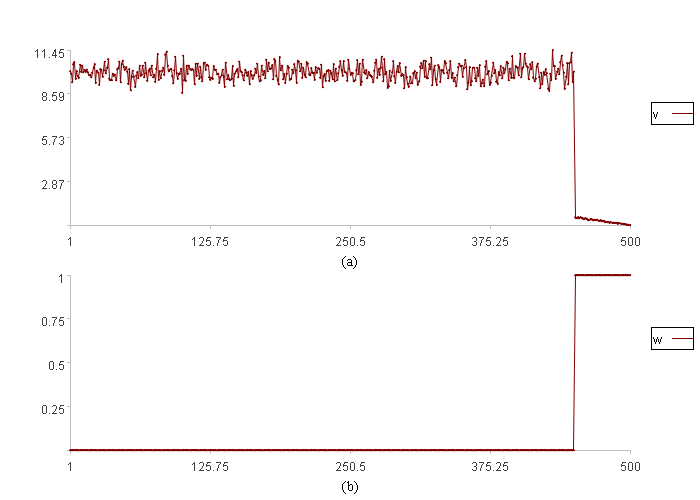
图(a)中v是数据取值。
图(b)中w是数据异常程度。
变化越界
数据走势图:
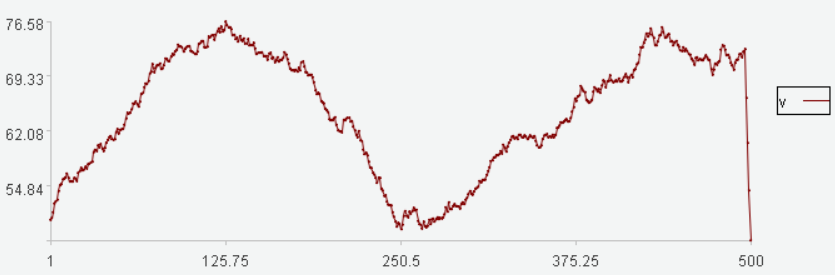
相较于其他数据的变化速度,最后几个数据变化过快,需要用变化率这个数学量来发现异常。
示例代码:
A |
B |
C |
D |
|
1 |
change_rate.json |
|||
2 |
=json(file(A1).read()) |
/read data |
||
3 |
500 |
/learn_interval |
||
4 |
box |
/method |
||
5 |
=A2.to(500) |
/learndata |
||
6 |
10 |
|||
7 |
=to(A6+1).(~|1) |
|||
8 |
=(A5.to(A6).rvs()|A5).(if(#<=A6,null,(s=~[-A6:0],linefit(A7,s).~.~))).to(A6+1,) |
/change_rate |
||
9 |
=A2.to(501,) |
/predictdata |
||
10 |
=[] |
|||
11 |
=[] |
|||
12 |
=[] |
|||
13 |
for A9 |
=s.insert(0,A13).delete(1) |
||
14 |
=linefit(A7,B13).~.~ |
/change_rate |
||
15 |
=A8.insert(0,B14).delete(1) |
|||
16 |
if A4=="box" |
=box(B15,B14,3) |
/tu,td,p |
|
17 |
=A10.insert(0,C16(1)) |
|||
18 |
=A11.insert(0,C16(2)) |
|||
19 |
=A12.insert(0,C16(3)) |
|||
20 |
else if A4=="dense" |
=dense(B13.([~]),[A13],[[0,100]],[2],1) |
/dense,p |
|
21 |
=A12.insert(0,C20) |
|||
22 |
=A12 |
|||
范围分布报警结果:
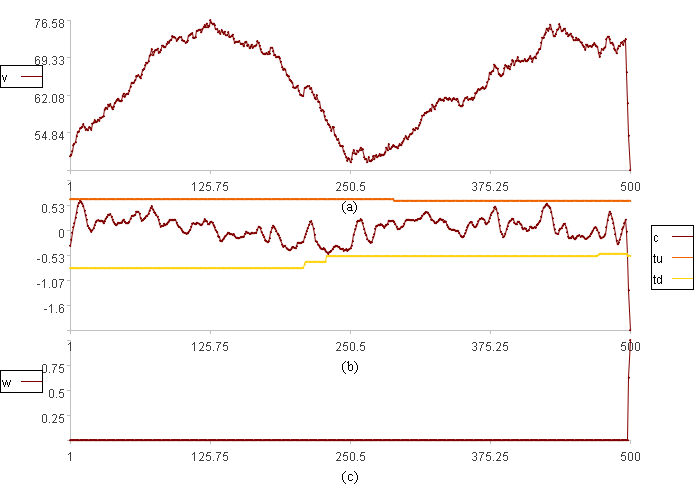
图(a)中v是数据取值。
图(b)中c是变化率,tu是变化率范围上限,td是变化率范围下限
图(c)中w是数据异常程度。
概率密度分布报警结果:
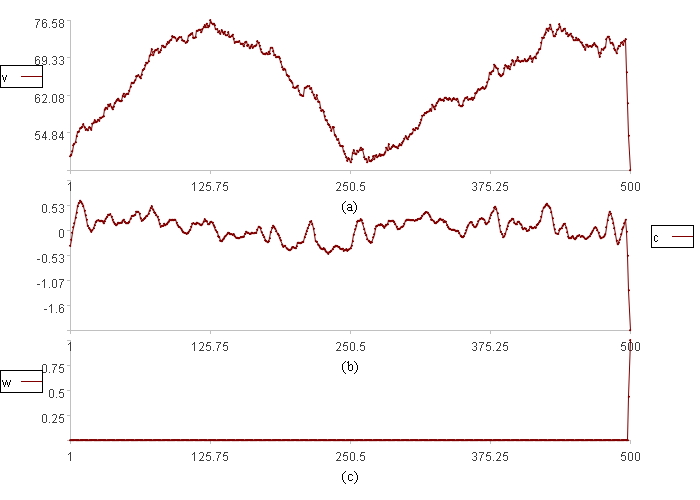
图(a)中v是数据取值。
图(b)中c是变化率。
图(c)中w是数据异常程度。
周期缺失
数据走势图:
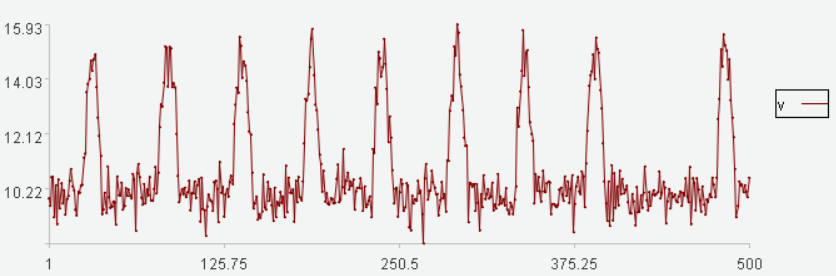
相较于其他数据,数据后半段缺失了一个周期凸起,可以用离散程度来发现该异常。
示例代码:
A |
B |
C |
D |
|
1 |
cycle_miss.json |
|||
2 |
=json(file(A1).read()) |
/read data |
||
3 |
500 |
/learn_interval |
||
4 |
box |
/method |
||
5 |
=A2.to(500) |
/learndata |
||
6 |
50 |
|||
7 |
=to(A6+1).(~|1) |
|||
8 |
=(A5.to(A6).rvs()|A5).(if(#<=A6,null,(s=~[-A6:0],sqrt(var(s))))).to(A6+1,) |
/std |
||
9 |
=A2.to(501,) |
/predictdata |
||
10 |
=[] |
|||
11 |
=[] |
|||
12 |
=[] |
|||
13 |
for A9 |
=s.insert(0,A13).delete(1) |
||
14 |
=sqrt(var(B13)) |
/std |
||
15 |
=A8.insert(0,B14).delete(1) |
|||
16 |
if A4=="box" |
=box(B15,B14,3) |
/tu,td,p |
|
17 |
=A10.insert(0,C16(1)) |
|||
18 |
=A11.insert(0,C16(2)) |
|||
19 |
=A12.insert(0,C16(3)) |
|||
20 |
else if A4=="dense" |
=dense(B13.([~]),[A13],[[0,100]],[2],1) |
/dense,p |
|
21 |
=A12.insert(0,C20) |
|||
22 |
=A12 |
|||
范围分布报警结果
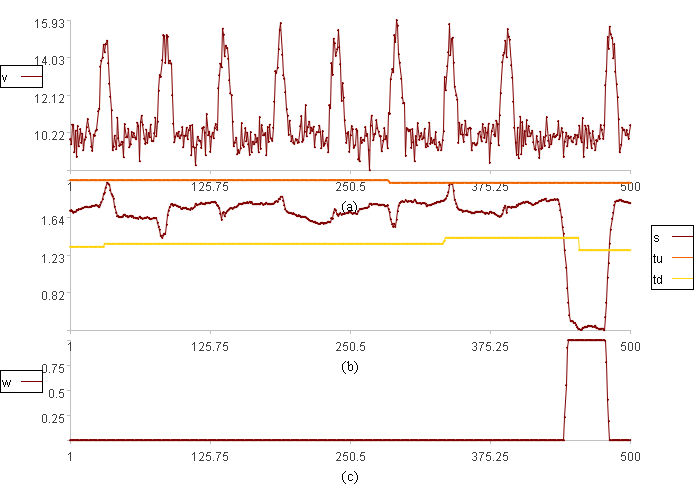
图(a)中v是数据取值。
图(b)中s是变化率,tu是离散程度范围上限,td是离散程度范围下限
图(c)中w是数据异常程度。
概率密度分布报警结果:
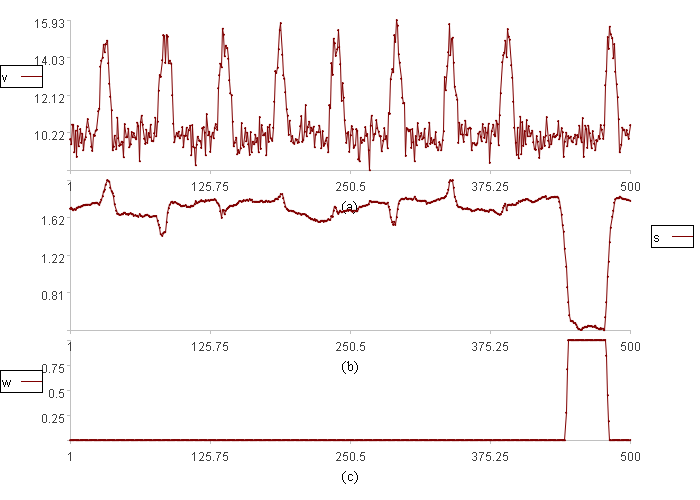
图(a)中v是数据取值。
图(b)中s是离散程度。
图(c)中w是数据异常程度。
梯度分布
数据走势图:
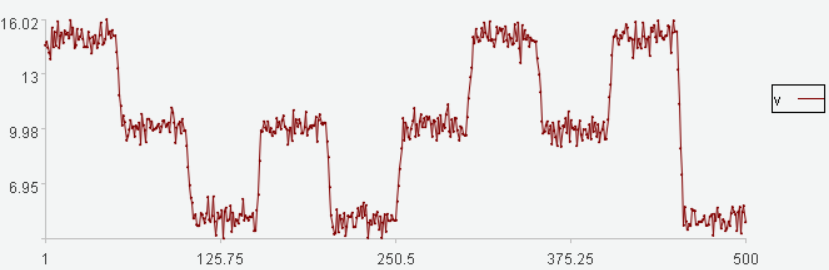
数据本来是3个阶梯连续变化的,可是在最后一次变化时,发生了跳变,这是之前没有发生过的,应该被视为异常。
示例代码:
A |
B |
C |
|
1 |
grad_dtr.json |
||
2 |
=json(file(A1).read()) |
/read data |
|
3 |
500 |
/learn_interval |
|
4 |
=A2.to(500) |
/learndata |
|
5 |
50 |
||
6 |
=to(A5+1).(~|1) |
||
7 |
=(A4.to(A5).rvs()|A4).(if(#<=A5,null,(s=~[-A5:0],s.m(-1,1)))).to(A5+1,) |
/grad |
|
8 |
=A2.to(501,) |
/predictdata |
|
9 |
=[] |
||
10 |
=[] |
||
11 |
=[] |
||
12 |
for A8 |
=s.insert(0,A12).delete(1) |
|
13 |
=s.m(-1,1) |
/grad |
|
14 |
=A7.insert(0,[B13]).delete(1) |
||
15 |
=dense(B14,B13,[[0,20],[0,20]],[2,2],1.5) |
/dense,p |
|
16 |
=A11.insert(0,B15) |
||
17 |
=A11 |
||
概率密度分布报警结果:
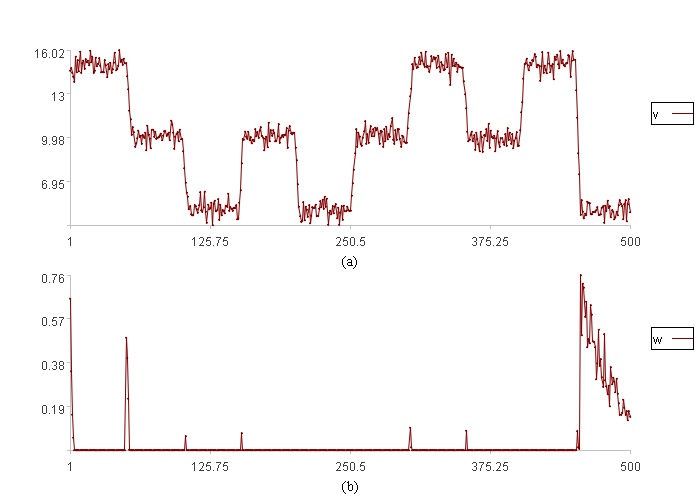
图(a)中v是数据取值。
图(b)中w是数据异常程度。
多维情况
工业生产中有时需要同时监控多块仪表才能发现异常,这时就需要发现多维时间序列的异常。
我们把多维异常分为两类:
1. 综合异常,将多个单维数据的异常合并成一个综合异常。
2. 联合异常,单维正常,但多维联合起来却异常。
综合异常
想把单维数据的异常综合成一个异常程度,最朴素的想法是为每个维度赋予权重,将每个维度的异常程度加权后相加即得到综合异常程度,但权重怎么计算呢?
是经常异常的维度权重高还是不常异常的维度权重高呢,我们可以借鉴 “幸存者偏差”的思想,它是二战时期盟军关于飞机防护提出的,经常异常的维度就像是飞回来的飞机身上满是弹孔的位置(比如机身),后续异常也不会产生多大影响,不常异常的维度就像是没有弹孔的位置(比如引擎),一旦异常就可能严重影响生产。所以应该是不常异常的维度权重高。
综合异常的计算过程如下:
各维度异常度:O=[o1,o2,…,om]
各维度权重:W=[w1,w2,…,wm],wi是幸存者偏差原理计算出来的。
综合异常度: 
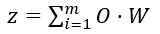
举例
三维数据各自的走势及报警图:
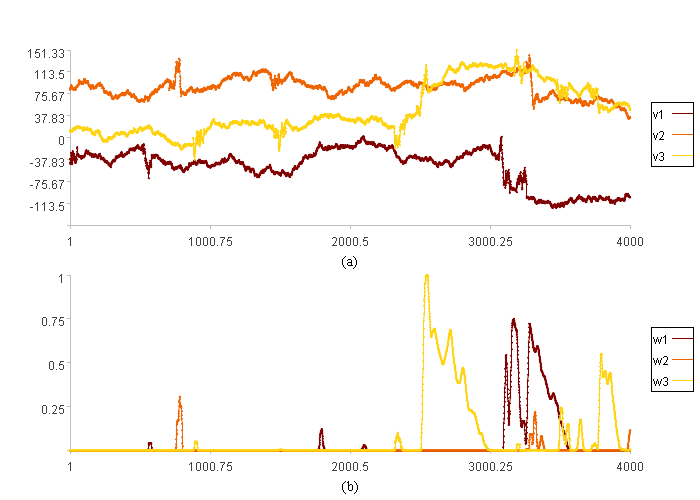
图(a)是三维数据走势图
图(b)是三维数据的报警图
示例代码:
A |
B |
C |
D |
|
1 |
mult_com.json |
|||
2 |
=json(file(A1).read()) |
/read data |
||
3 |
1000 |
/learn_interval |
||
4 |
=A2.to(A3) |
/learndata |
||
5 |
=A2.to(A3+1,) |
/predictdata |
||
6 |
=[] |
/org |
||
7 |
=[] |
/warn |
||
8 |
=[] |
/weight |
||
9 |
=[] |
/comp warn |
||
10 |
=weight=null |
|||
11 |
=transpose(A4) |
|||
12 |
for A5 |
=#A12 |
||
13 |
=[] |
|||
14 |
for A12 |
=#B14 |
||
15 |
=A11(C14).insert(0,B14).delete(1) |
|||
16 |
=dense(C15.([~]),[B14],[[-200,200]],[20],1.5) |
/dense,p |
||
17 |
=B13.insert(0,C16) |
|||
18 |
=A6.insert(0,[B13]) |
|||
19 |
=A6.to(max(1,B12-20),B12) |
/org |
||
20 |
=if(B12==1,B19,mmean(B19)).~ |
/warn |
||
21 |
=A7.insert(0,[B20]) |
|||
22 |
if B12==1 |
=weight=(lth=B20.len(),B20.(1/lth)) |
||
23 |
else if B20.count(~>0)==0 |
=A7.to(max(1,B12-A3),B12) |
||
24 |
=weight=warn_weight(C23) |
|||
25 |
else |
=weight |
||
26 |
=A8.insert(0,[weight]) |
|||
27 |
=(B20**weight).sum() |
/comp warn |
||
28 |
=A9.insert(0,B27) |
|||
29 |
=A9 |
|||
A14代码块:密度分布法计算异常程度。
B22-B26:幸存者偏差法计算权重
综合异常图:
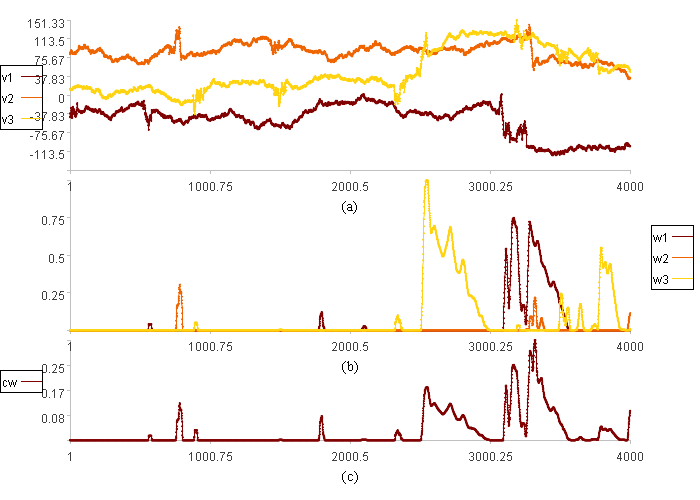
图(a)是三维数据走势图
图(b)是三维数据的报警图
图(c)是综合异常程度
红框位置两个维度出现异常,综合异常程度更高。
联合异常
有些位号,单维看起来正常,但合在一起看就异常。
可以分为两种情况:
1. 有相关关系,即两个位号存在某种关联关系,当关联关系变化时被认为是异常。
2. 未知关联关系,这类异常不容易发现,但可以将多维数据看作空间中的点,出现概率低的点被认为是异常。
有关联关系
工业生产中,有些位号是存在关联关系的,比如阀门开度和流量,阀门开度大,流量就大,阀门开度小,流量就小。下图是某工厂阀门开度和流量的数据:
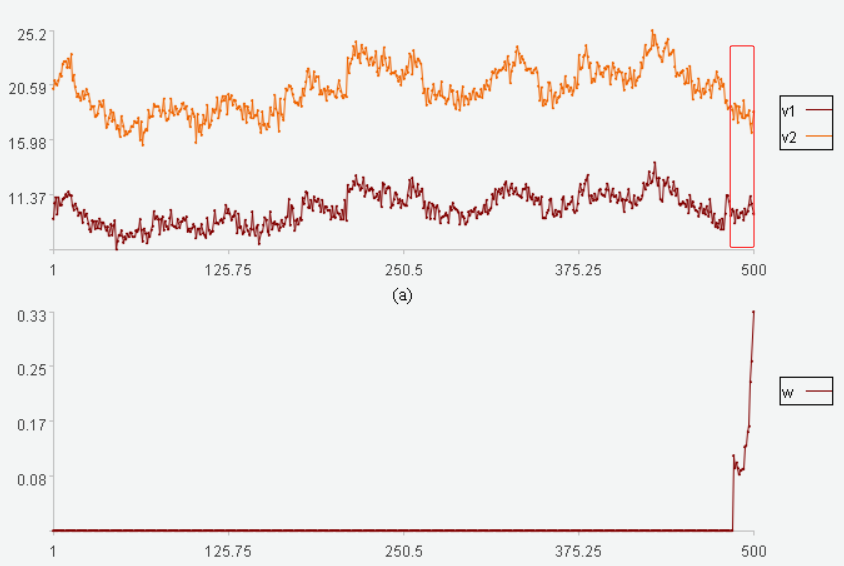
图中v2是阀门开度,v1是流量,红框中两者的关系发生变化,阀门开度增大,流量却在减小,异常了。
用一种数学量表示两者的相关系,就可以延用单维的异常发现方法发现异常了。
示例代码:
A |
B |
C |
D |
|
1 |
2d_cor.json |
|||
2 |
=json(file(A1).read()) |
/read data |
||
3 |
500 |
/learn_interval |
||
4 |
box |
/method |
||
5 |
=A2.to(500) |
/learndata |
||
6 |
30 |
|||
7 |
=(A5.to(A6).rvs()|A5).(if(#<=A6,null,(s=~[-A6:0],linefit(s.(~(1)|1),s.(~(2))).~.~))).to(A6+1,) |
/corr |
||
8 |
=A2.to(501,) |
/predictdata |
||
9 |
=[] |
|||
10 |
=[] |
|||
11 |
=[] |
|||
12 |
for A8 |
=s.insert(0,[A12]).delete(1) |
||
13 |
=linefit(B12.(~(1)|1),B12.(~(2))).~.~ |
/corr |
||
14 |
=A7.insert(0,B13).delete(1) |
|||
15 |
if A4=="box" |
=box(B14,B13,3) |
/tu,td,p |
|
16 |
=A9.insert(0,C15(1)) |
|||
17 |
=A10.insert(0,C15(2)) |
|||
18 |
=A11.insert(0,C15(3)) |
|||
19 |
else if A4=="dense" |
=dense(B14.([~]),[B13],[[-10,10]],[0.5],1.5) |
/dense,p |
|
20 |
=A11.insert(0,C19) |
|||
21 |
=A11 |
|||
范围分布报警结果:
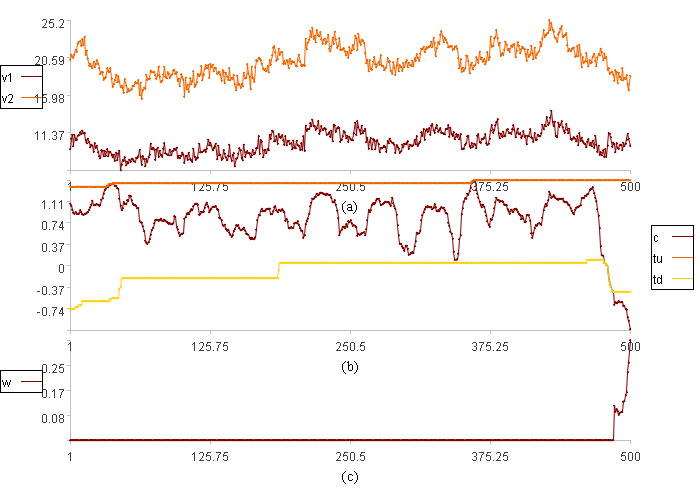
图(a)中v2是阀门开度,v1是流量。
图(b)中c是关联关系,tu是关联关系范围上限,td是关联关系范围下限
图(c)中w是数据异常程度。
概率密度分布报警结果:
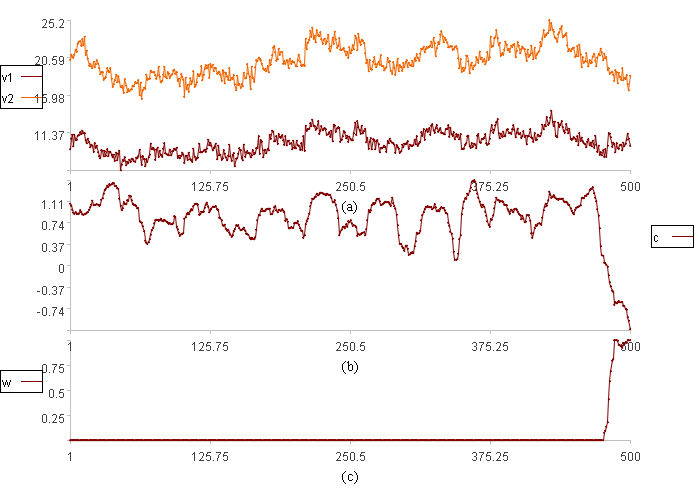
图(a)中v2是阀门开度,v1是流量。
图(b)中c是关联关系。
图(c)中w是数据异常程度。
未知关联关系
未知关联关系的数据不容易发现异常,但回到异常的定义:未发生过或者少发生的情况是异常。
为了便于可视化,我们以二维数据为例来介绍,数据如下:
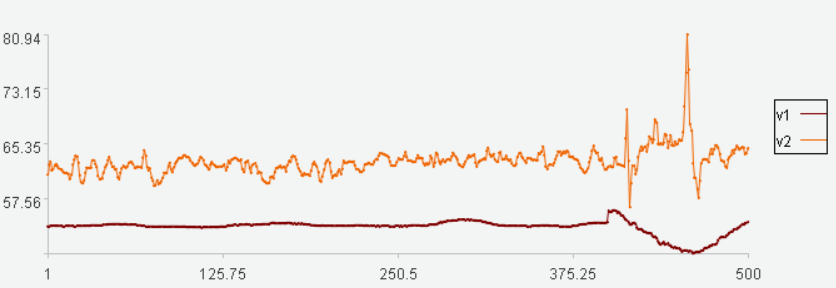
相较于其他位置,数据后半段没有发生过这些情况,把两个维度用散点图表示出来如下图:
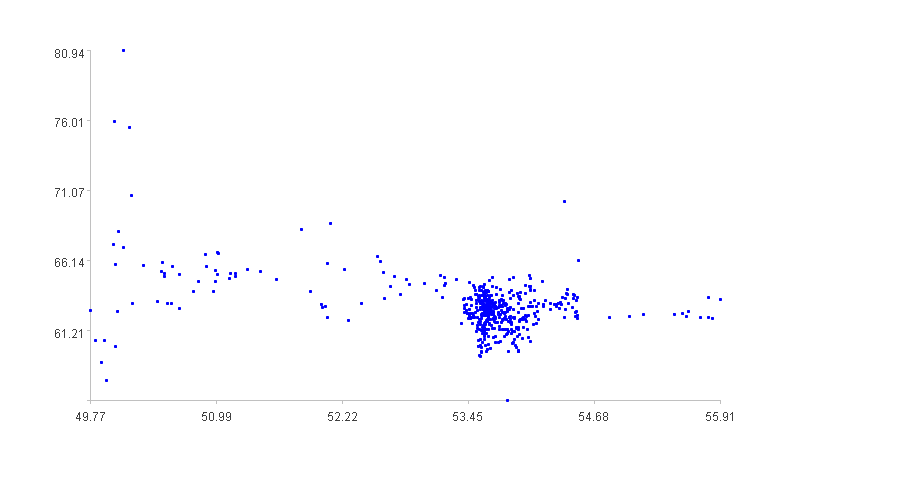
横轴是维度1数据,纵轴是维度2数据。
从散点图不难看出,多数数据比较集中,少数数据分散,分散数据就是少出现的情况,将其找出来作为异常。
示例代码:
A |
B |
C |
|
1 |
no_cor.json |
||
2 |
=json(file(A1).read()) |
/read data |
|
3 |
500 |
/learn_interval |
|
4 |
=A2.to(500) |
/learndata |
|
5 |
50 |
||
6 |
=A2.to(501,) |
/predictdata |
|
7 |
=[] |
||
8 |
for A6 |
||
9 |
|||
10 |
=A4.insert(0,[A8]).delete(1) |
||
11 |
=dense(B10,A8,[[0,100],[0,100]],[1,5],1) |
/dense,p |
|
12 |
=A7.insert(0,B11) |
||
13 |
=A7 |
||
报警结果:
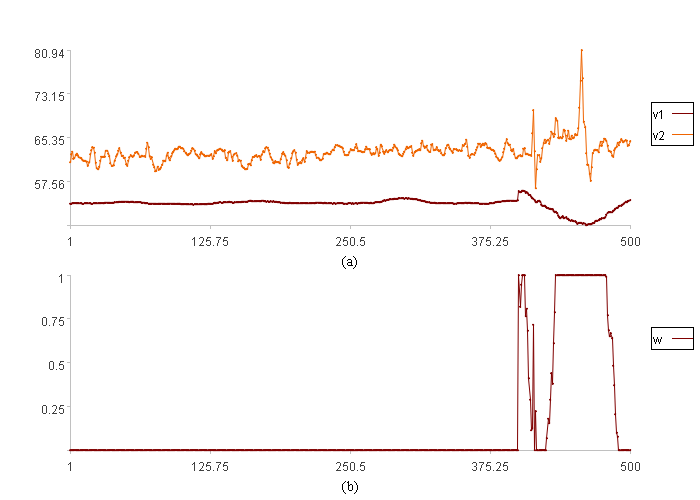
图(a)中是两个维度数据取值。
图(b)中w是数据异常程度。
如果把异常程度大于0的数据作为异常点,散点图中的异常情况如下:
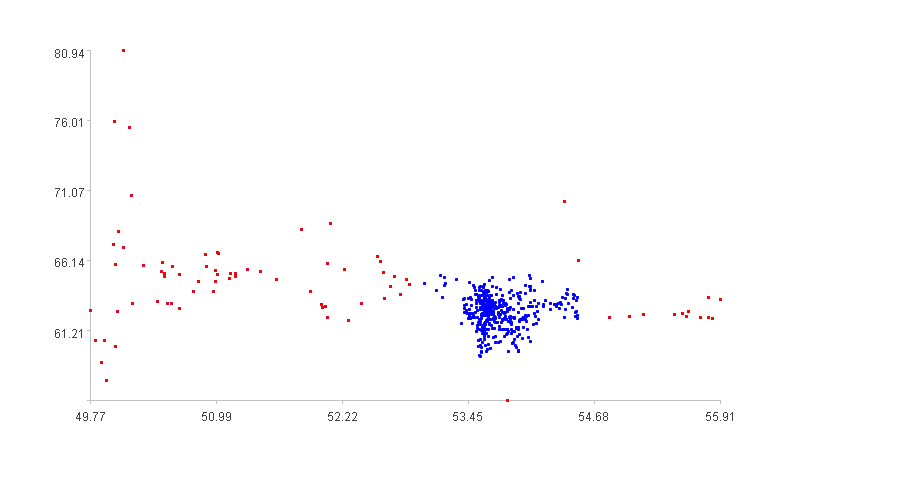
图中红色点对应走势图中异常程度大于0的数据。
总结
基于以上实践,我们自研的工业 AI 监盘异常发现算法已在多种工业场景中得到有效验证。该算法立足于“异常即罕见”的核心思想,借助动态分布建模与多维度联合分析,实现了在无标注条件下的高精度异常识别。其主要优势可总结如下:
1. 完全无监督,无需标注数据
算法基于设备正常运行状态下数据模式相对稳定的假设,通过对历史数据分布的自主学习,自动识别偏离该分布的异常点,彻底摆脱了对人工标注数据的依赖,极大降低了实施成本与数据准备周期。
2. 高实时性与低资源消耗
算法采用轻量化设计与局部动态建模机制,无需复杂模型训练与微调过程,可在数据采集后立即进行异常判断,满足在线任务对高时效性的严苛要求,能够在单台 12C32G 的服务器上完成上千时间序列 5 秒频率的异常发现任务。
3. 可靠性高且可优化
算法的判断基于清晰的历史数据分布与严密的数学逻辑,过程透明、结果可复现、可验证,保障了高可靠性。同时,系统支持现场工程师结合深入的工艺知识,对关键参数进行调整与校准,实现算法效果在现场的持续优化,越用越精准。
4. 多场景适应性与灵活扩展能力
算法支持包括值越界、变化越界、周期缺失、梯度跳变等多种异常类型的检测,不仅能够识别各维度独立异常,更能发现多维度数据变化而导致的联合异常,从而在看似正常的单维数据中捕捉系统级异常,增强了复杂系统中隐性故障的发现能力。
本算法以“异常是历史中未发生或少发生的情况”为根本出发点,结合工业数据的时序特性与多维关联特点,构建了一套完整、轻量且可扩展的无监督异常发现体系,为工业设备的高效、可靠监控提供了切实可行的技术路径。



