线性回归指标
在股市投资中,投资者往往需要根据历史数据来预测未来的市场趋势,以便做出更明智的投资决策。线性回归作为一种经典的统计工具,在股票量化策略中发挥着举足轻重的作用,它通过对历史数据进行统计分析,建立出一个尽可能反映市场规律的模型,从而预测未来的股票价格走势。
建立线性模型的主要思路为:
1. 确定自变量和因变量。因变量一般就是每日的股票价格,如收盘价;自变量可以是价格、财务指标、量化因子等等。
2. 确定训练数据和预测数据的天数,取前 n 天数据做训练,近 m 天数据做预测。例如取前 n 天数据训练,近 m 天数据预测
3. 对自变量特征进行 PCA 主成分分析,提取前 k 个主要成分。
4. PCA 降维之后,用 linefit() 函数做线性回归的预测模型。
5. 在预测数据上做预测,得到第二天的股票价格
指标参数:
y |
指标返回列,模型预测的股票价格 |
n |
数字,训练数据天数 |
m |
数字,预测数据天数 |
k |
数字,主成分个数,缺省值为 4 |
函数代码:
A |
B |
|
1 |
func PCALF(A, $y, n, m, k=4) |
=A.derive@o(~[-m+1:0].conj([开盘,收盘,最高,最低]):PCALF0) |
2 |
=A.run( if( #>n+m, ( ox=PCALF0[-n:-1], tm=pca(ox, k), tx=pca(ox, tm), ty=收盘[-n+1,0], mc=linefit(tx.(~|1), ty ), d=pca([PCALF0], tm ).(~|1),${y}=mul(d, mc) ))) |
|
3 |
=A.alter(; PCALF0) |
这段代码中 pca 函数来自于数学库,读者使用时要在工具→选项菜单中加载数学库。
B49 格中的“[开盘, 收盘, 最高, 最低]”是建模的自变量,读者可以自行修改。
举例:调用脚本计算浦发银行 2024 年的线性回归指标。n 取 100,m 取 5。
A |
B |
|
… |
… |
… |
5 |
=call@f("indicator.splx") |
登记脚本中的函数 |
6 |
… |
计算出源数据 |
7 |
=A6.derive(:LF) |
增加要返回的指标字段 |
8 |
=PCALF(A7, LF, 100, 5) |
调用函数计算指标 |
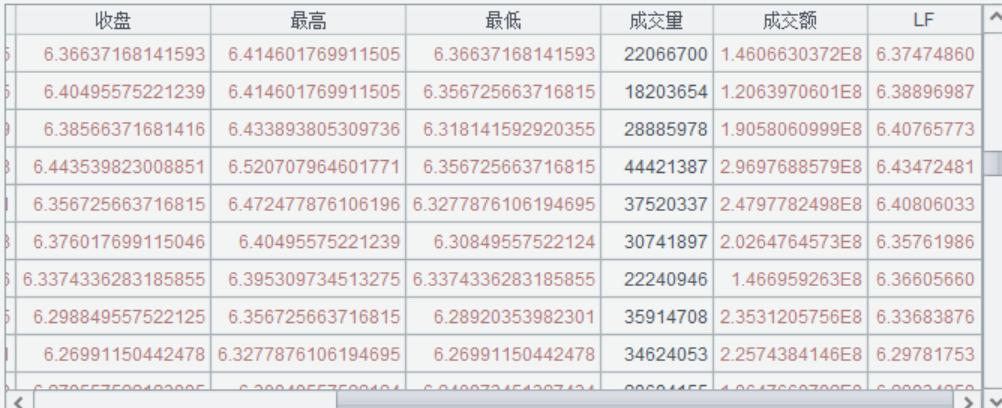
运行效果:
指标应用说明:第 14 章 线性回归预测策略 - 乾学院



