SPL 量化 复权数据
复权概念
由于股票经常发生分红、配股、分拆或合并等事件,使得股价出现较大变化,复权就是用来修正这种股价变化。
例如某支股票每股 10 元,持有 100 股,总资产 1000 元
发生拆股后,持有的 100 股变为 500 股,但是股价也会自动调整为原来的 1/5,变为 2 元,总资产还是 1000 元,并没有发生变化。
股价从 10 元变为 2 元,看似暴跌了 80%,但投资者的资产始终没变,因此股价的变化其实是 0。
为了避免这种价格“暴跌”的影响,需要对股票的价格进行修复,这一过程就叫做复权。
复权分为前复权和后复权。
前复权就是保持新时间点的价格不变,对历史时间点的价格进行调整,使得股价连续。而后复权正好相反,保持早期时间点价格不变,调整后续时间点的价格。
按上面例子,股价从 10 元变为 2 元,向前复权时,会维持今天的股价不变,而把昨天的股价由 10 元变成 2 元与当前价格保持一致,之前的股价也都一律按比例缩小,股价变为一条连续的曲线。
反之,向后复权就是保持昨天的价格 10 元不变,调整当前价格 2 元变 10 元,之后的股价也都按比例增大。
复权价的计算方法有多种,由于数据口径或计算方法的不同,得到的复权价格也会有所不同。这里我们采用的是涨跌幅复权法。
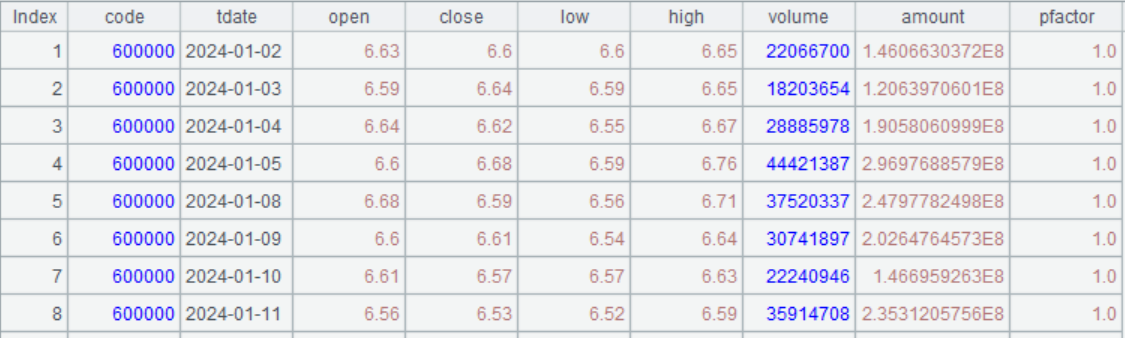
日 K 线数据里,pfactor 为复权因子。需要注意的是:该复权因子为当日复权因子,而不是累计复权因子,这样的好处是更方便随意指定一个时间区间计算出和该区间相关的复权价格。累计复权因子计算的是从头向后复权或从尾向前复权,这会导致距离太远的数会太大或太小,和实际的股票价格相差很大,有些软件还会算出负数。而当日复权因子则可以只计算所需区间的复权价格,计算量小,也不会和实际股票相差很多,用起来更灵活。因此这里我们采用当日复权因子。
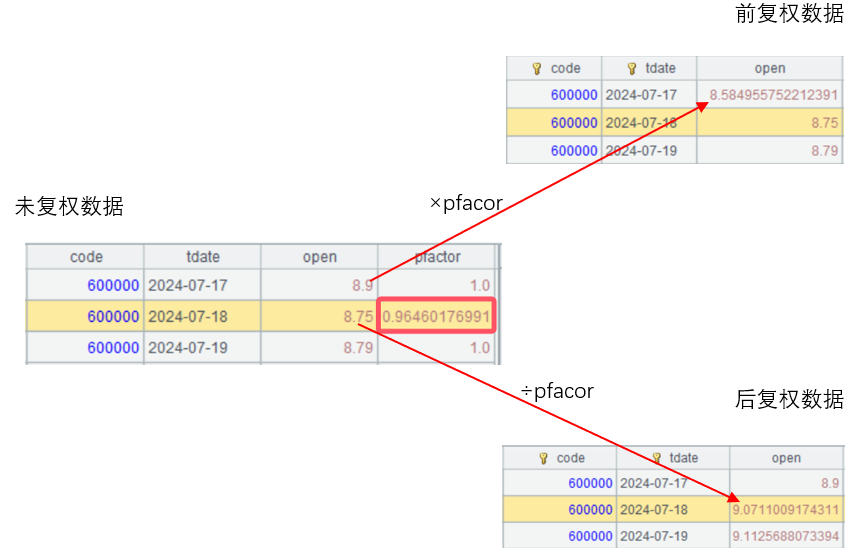
比如以浦发银行为例,数据如下图所示。在 2024 年 7 月 18 日发生了复权动作,复权因子 pfactor 为 0.96460176991。前复权数据就是保持当日股价不变,昨日股价调整为 8.9*0.96460176991=8.584955752212391,以此类推,之前的股价也按比例调整。反之,后复权数据就是保存历史股价不变,当日股价调整为 8.75/0.96460176991=9.0711009174311,之后的股价同样也按比例调整。
由图中也可以看出 pfactor 为当日复权因子,只有在发生复权动作时参数才会变,其余都是 1。网上有些渠道提供的因子可能为累计因子,因此看起来会有所不同,使用时需注意区分。
复权价格
因为复权后价格才有涨跌的可比性,所以做量化策略时通常会使用复权价格,我们可以写一个脚本实现从原始价格到复权价格的计算。
复权脚本:
A |
B |
|
1 |
for data.group(code) |
=A1.sort(tdate).(pfactor) |
2 |
=if(opt=="b",B1.(if(#==1,cp=1,cp=cp/~)), B1.rvs().(if(#==1,cp=1,cp=cp*~[-1])).rvs()) |
|
3 |
=A1.run(cp=B2(#), open*=cp, close*=cp, low*=cp,high*=cp ) |
|
4 |
return data |
脚本参数:
参数名 |
含义 |
opt |
复权类型。填空:前复权,”b”: 后复权; |
dada |
某支或多支股票的 k 线数据 |
将此脚本保存为 adjustprice.splx,可返回股票的前复权或后复权数据。
例如,计算浦发银行 2024 年的复权价格:
A |
B |
|
1 |
=register("loadkday","loadkday.splx") |
将读数脚本登记为函数 |
2 |
=register@o("adjustprice," adjustprice.splx") |
将复权脚本登记为函数,并将第一个参数设为选项 |
3 |
600000 |
股票代码。计算多支股票时传入代码序列如 [600000,600015] |
4 |
2024-01-01 |
开始日期 |
5 |
2024-12-31 |
截止日期 |
6 |
=loadkday(A3,A4,A5) |
读取 k 线数据 |
7 |
=adjustprice(A6) |
返回前复权 |
8 |
=loadkday(A3,A4,A5) |
读取 k 线数据 |
9 |
=adjustprice@b(A8) |
加选项 @b 返回后复权 |
运行效果:
A7 前复权
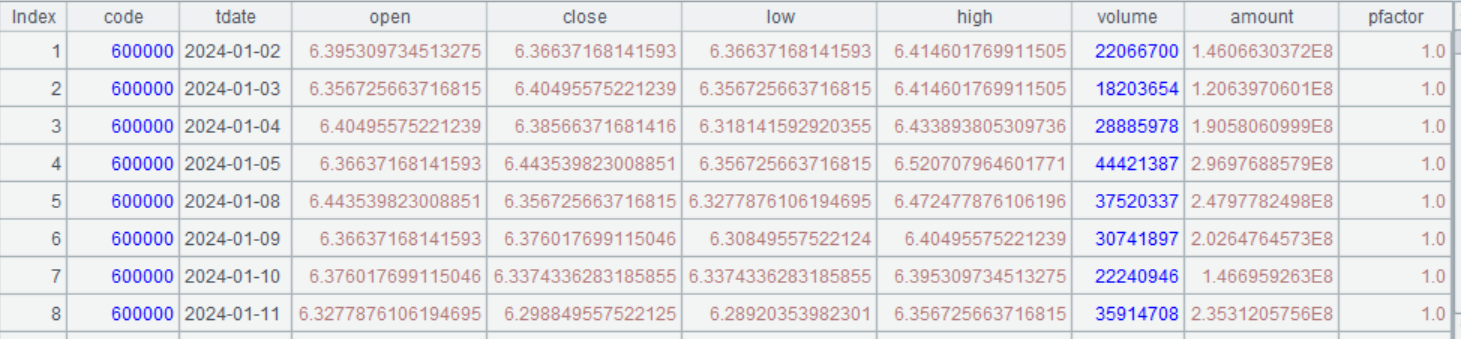
A8 后复权