变量相关性分析—Pearson and Spearman
相关性分析是数据分析和挖掘中经常用的方法,通过对特征和目标之间的关系分析可以发现业务运营中的影响因素,并对业务的发展进行预测。
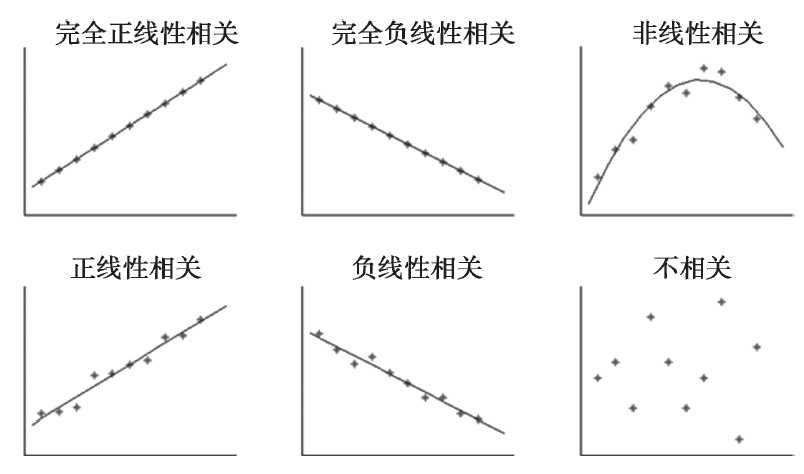
两个变量之间的关系有以下几种:
(1) 完全正线性相关:一个值随着另一个值的增加而增加,两者的关系完美的落在一条斜率大于 0 的直线上
(2) 完全负线性相关:一个值随着另一个值的增加而减少,两者的关系完美的落在一条斜率小于 0 的直线上
(3) 非线性相关:两个变量之间没有明显的线性关系,却存在着某种非线性关系,比如:曲线,S 型,Z 型等等
(4) 正线性相关:一个值随着另一个值的增加而增加,两者的关系近似的落在一条斜率大于 0 的直线上
(5) 负线性相关:一个值随着另一个值得增加而减少,两者的关系近似的落在一条斜率小于 0 的直线上
(6) 不相关:两者之间没有相关性
在实际应用中我们可以通过相关系数来分析两变量之间的相关程度,常用的相关系数为 Pearson 和 Spearman 相关系数
1. Pearson 相关系数
皮尔逊相关也称为积差相关(或积矩相关),是英国统计学家皮尔逊于 20 世纪提出的一种方法。它用来计算两个变量之间线性相关性。
计算公式为:
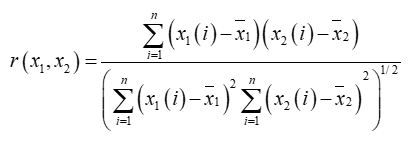
Pearson 相关系数的取值范围为 [-1,1],绝对值越接近 1,相关性越强;绝对值越接近 0,相关性越弱。它是评估线性相关的指标,适用于连续变量,成对数据,总体呈正态分布的数据。
2. Sprarman 相关系数
Spearman 又称秩相关系数,以 Charles Spearman 命名,是基于数据值次序的非参数关联度量。公式是:
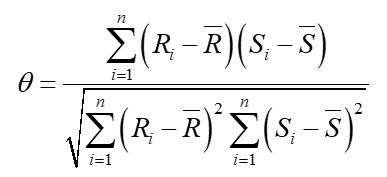
Spearman 系数的取值范围为 [-1,1],绝对值越接近 1,相关性越强绝对值越接近 0,相关性越弱。Spearman 用来评估单调关系(无论是否线性),既适用于连续变量也适用于分类变量,对变量总体分布形态,样本容量大小无要求
Pearson 用来评估两个变量之间的线性关系,而 Spearman 评估的是单调关系。
两者的关系可以用下面几个例子来解释。
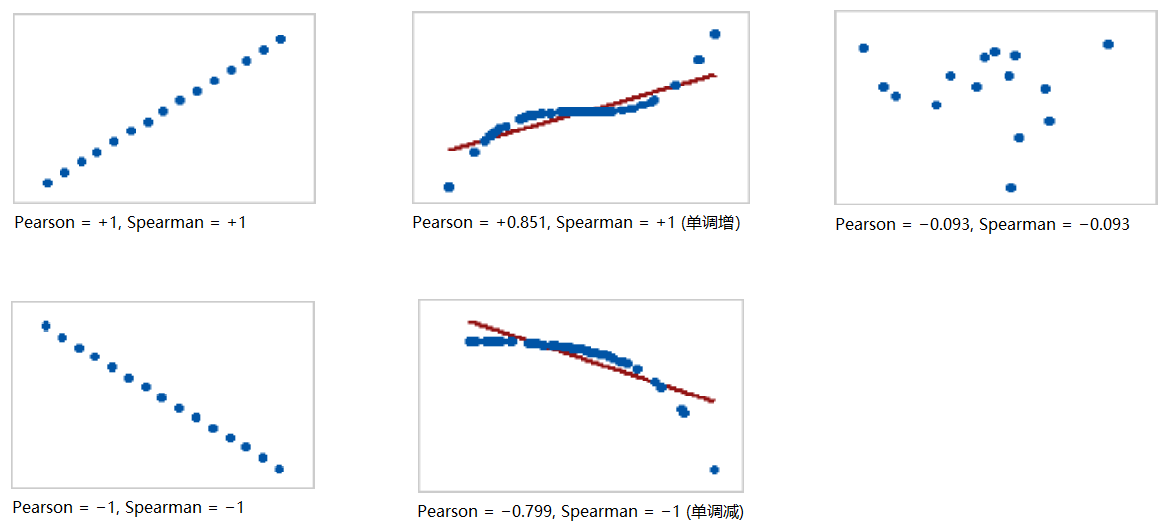
3. 应用举例
下面我们通过一个例子来看下如何分析两变量的关系。
以来自于 Kaggle 上房价预测的数据为例,分析“GrLivArea”居住面积和“SalePrice”房屋的销售价格是否相关。
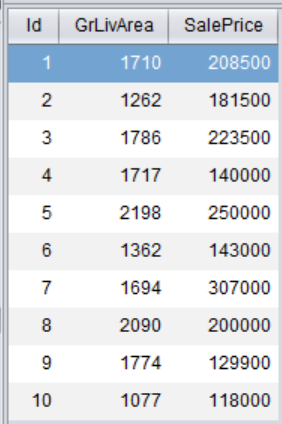
数据分析通常是一个边分析边计算的过程,可以用交互性更强的 SPL 来实现。
首先将数据导入到 SPL,画散点图,观察两变量之间的关系
SPL 代码:
A |
|
1 |
=file("house_prices_train.csv").import@tc() |
2 |
=A1.(GrLivArea) |
3 |
=A1.(SalePrice) |
4 |
=canvas() |
5 |
=A4.plot("NumericAxis","name":"x") |
6 |
=A4.plot("NumericAxis","name":"y","location":2) |
7 |
=A4.plot("Dot","lineWeight":0,"lineColor":-16776961,"markerWeight":1,"axis1":"x","data1":A2,"axis2":"y","data2": A3) |
8 |
=A4.draw(800,400) |
A1 导入数据
A2 居住面积变量

A3 销售价格变量
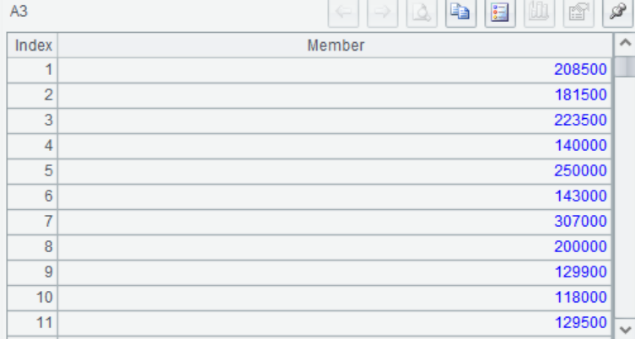
A4-A8 以居住面积为 x 轴,销售价格为 y 轴,画散点图
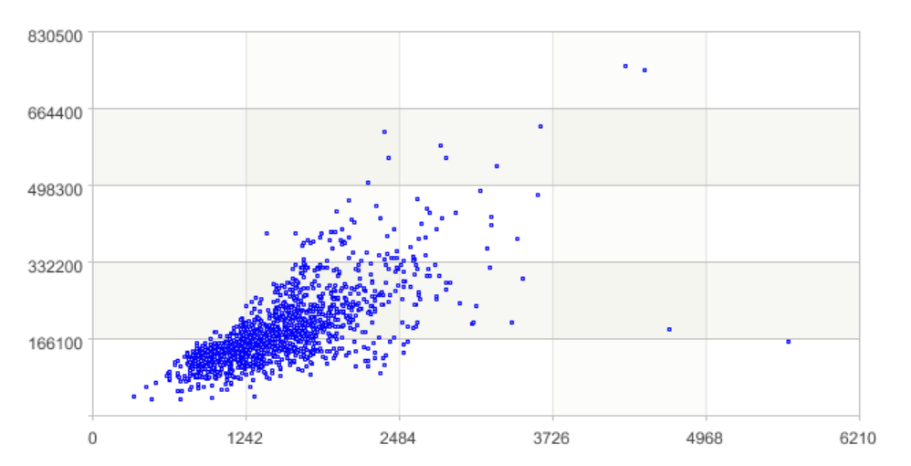
从散点图上可以看到房屋的居住面积和销售价格之间存在线性递增的关系。因此可以尝试用 pearson 和 spearman 来计算相关性。
继续写代码:
A |
|
… |
…… |
9 |
=pearson(A2,A3) |
10 |
=spearman(A2,A3) |
A9 计算 pearson 相关系数

A10 计算 spearman 相关系数

由结果可知,房屋居住面积和销售价格之间存在较强的线性关系。
在回归分析或线性拟合时,有时会对数据进行预处理来进一步增强这种线性关系。例如本例我们可以对数据进行一个纠偏处理然后再观察它们之间的线性关系。
SPL 里有一些自动预处理的函数,用起来很方便。
继续写代码:
A |
|
… |
…… |
11 |
=A2.skew() |
12 |
=A3.skew() |
13 |
=A2.corskew() |
14 |
=A3.corskew() |
15 |
=pearson(A13(1),A14(1)) |
A11-A12 分别计算两个变量的偏度


两个变量的偏度有点大,并非一个标准的正态分布。
A13-A14 自动纠偏
A15 计算纠偏后的 pearson 相关系数

可以看到,经过处理后变量之间的线性关系增强,更方便做一进步的拟合计算。




英文版