SPL 量化系列实践:凯利公式和仓位管理
凯利公式(Kelly Criterion)是一种根据赌博赢或输的概率,计算出每次下注的资金占所有赌本的最佳比例的公式。它适用于只有2种结果的简单赌局:要么输掉所有本金,要么赢得本金乘以特定赔率。公式的一般性陈述为:
f=(bp-q)/b (公式一)
其中,f是现有资金应进行下次投注的比例;
b是投注可得的赔率(不含本金);
p是获胜率;
q是落败率,即1-p。
举例而言,若一赌博有60%的获胜率(p=0.60,q=0.40),而赌客在赢得赌局时,可获得一赔一的赔率(b=1),则赌客应在每次机会中下注现有资金的20%(f=0.20),以最大化资金的长期增长率。如果赔率没有优势,即b<q/p,公式的结果是负的,那么建议不下注。如果赔率是负的,即b<0,也就是暗示应该下注到另外一边。
如果投资中,获胜率和失败率以及赔率和上面的赌局一样,那意味着投资者每次的投资比例只有20%,这会导致利润减少,无法让投资产生最大化的增长率。因为凯利公式的本质是对风险的管理,金融市场上有人更喜欢冒险,凯利公式还有一个衍生的变形公式可以供这类高风险偏好的人选择:
f=(pW-qL)/WL (公式二)
其中,f,p,q同公式一;
W是获胜后的净盈率;
L是失败后的净损率。
举例说明:投资者决定用10万元参与股票投资,30%的增长幅度止盈,20%的亏损幅度止损,最多盈利3万元,最多亏损2万元,这里W=0.30,L=0.20,仍然假设p=0.60,q=0.40,此时可以计算出最优仓位=(pW-qL)/WL=(0.6*0.3-0.4*0.2)/(0.3*0.2)=1.66,大于1理论上认为可以借钱建仓或加杠杆。
温馨提示:珍爱生命,远离杠杆!
在上述例子中,公式一每次只能两成仓位,公式二确是满仓进入。很明显,公式一中损失全部本金的情况在金融市场中很少发生(杠杆类不算),而公式二的情况其实并没有考虑到黑天鹅事件(突发事件导致连续跌停)的情况。也就是说,公式一的结论有些保守,而公式二的结论太过乐观。
既然黑天鹅事件不可避免,那么用投资组合的方式降低黑天鹅事件的影响会更加合理,如果有100万元本金,用来投资市场上最活跃(2023年5月6日至2023年5月6日交易量最大)的前5只股票,仓位应该怎么分配。
计算这5支股票近一年(12个月,2023年5月6日至2023年5月6日)的月收益情况,统计正收益月数(收益>=0)和负收益月数(收益<0),其中:
p=正收益月数/12;
q=负收益月数/12;
W=正收益月的月化收益率
L=负收益月的月化收益率
b=W/L
总资金仓位C:100万
5支股票的平均仓位=ag
投资股票的资金valb_cash=C*max(1,ag)(公式二计算出的仓位可能大于1,所以ag也可能大于1,但是我们不加杠杆,所以仓位最大是1,即满仓)。
剩余资金balance=C-valb_cash。
每支股票的仓位按占所有股票仓位之和的比重分配,比如A,B,C三支股票,计算出来的仓位是0.2,0.3,0.1,则A股票的仓位占比=0.2/(0.2+0.3+0.1)=0.33,这支股票可用的现金是valb_cash*0.33。
SPL代码
A |
B |
|
1 |
=directory("daily") |
|
2 |
=A1.(file("daily/"/~).cursor@tc().select@b(trade_date>20230506&&trade_date<=20240506).fetch@x()).select(~) |
|
3 |
=A2.select((output(#),filename@e(~.ts_code)!="BJ")) |
|
4 |
=A3.top(-5;~.sum(vol)) |
|
5 |
=create(ts_code,months,positive_num,negative_num,p,q,W,L,b,formula1,formula2) |
|
6 |
for A4 |
|
7 |
=A6.derive(if(#>1, close/ pre_close *factor[-1], close/pre_close):factor) |
|
8 |
=hfq_fst=B7(1),B7.new(date(string(trade_date);"yyyyMMdd"):trade_date,round(factor/hfq_fst.factor*hfq_fst.close,2): hfq_close) |
|
9 |
=code=filename@n(B7.ts_code) |
|
10 |
=st=B8.trade_date |
|
11 |
=et=B8.m(-1).trade_date |
|
12 |
=itv=interval@m(st,et) |
|
13 |
=seg_dt=st|itv.(elapse@m(st,~)) |
|
14 |
=gp=B8.group(seg_dt.pseg(trade_date):ID;~.m(-1).hfq_close/if(#!=1,~[-1].m(-1).hfq_close,~.hfq_close)-1:income_ratio) |
|
15 |
=B14.align@a([true,false],income_ratio>=0) |
|
16 |
=B15(1).len() |
|
17 |
=B15(2).len() |
|
18 |
=p=B16/12 |
|
19 |
=q=B17/12 |
|
20 |
=B15(1).(income_ratio).iterate(~~*(1+~),1) |
|
21 |
=B15(2).(income_ratio).iterate(~~*(1+~),1) |
|
22 |
=W=sqrt(B20,B16)-1 |
|
23 |
=L=abs(sqrt(B21,B17)-1) |
|
24 |
=b=abs(W/L) |
|
25 |
=fm1=(b*p-q)/b |
|
26 |
=fm2=(p*W-q*L)/(W*L) |
|
27 |
=A5.record([code,12,B16,B17,p,q,W,L,b,fm1,fm2]) |
|
28 |
1000000 |
|
29 |
=A5.select(formula1>0) |
|
30 |
=transpose(A29.([formula1,formula2])) |
|
31 |
=A30.((ag=~.avg(),valb_cash=A28*min(1,ag),s=~.sum(),~.(~/s*valb_cash)|(A28-valb_cash))) |
|
32 |
=transpose(A31) |
|
33 |
=(A29.(ts_code)|"banlance").new(~:code,A32(#)(1):pos1,A32(#)(2):pos2) |
|
A2:游标选出2023年5月6到2024年5月6日的股票行情数据
A3:过滤掉北京交易所的股票
A4:交易量最大的5支股票的行情数据
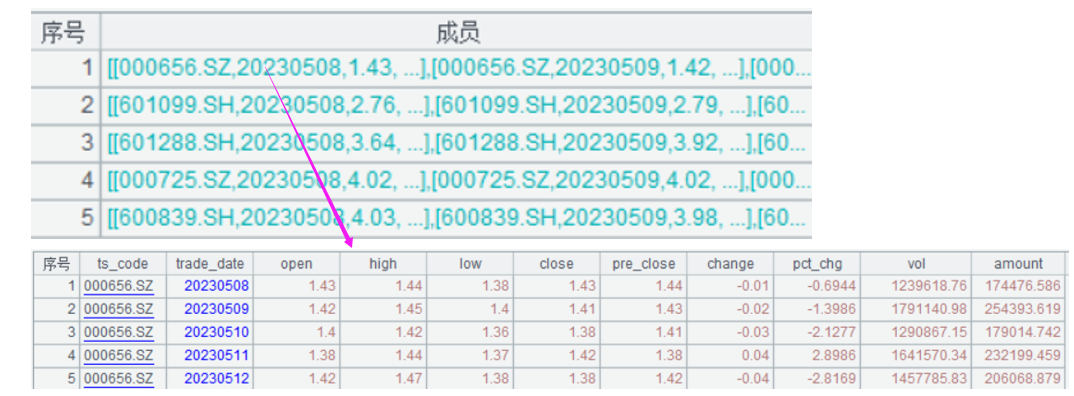
A5:初始化一个序表,用于存储各股票计算仓位需要的数据,包括p、q、W、L等。
A6代码块:循环每支股票计算仓位需要的数据。
B7、B8:后复权收盘价,方便计算收益率。
B10~B14:按不规则月份分组(前一个月6号以后到本月6号为1个月)。
量化交易中难免会遇到不规则月份分组,SPL通过pseg函数可以很轻松的完成分组认为(感兴趣的同学可以尝试用Python来写一下不规则月份分组的代码,两者对比一下)。
B15~B26:计算每组的p、q、W、L等数据。
B27:把数据存到A5初始化的序表中。
循环结束后,A5的数据:

A28:可用现金100万
A29:选出公式一的仓位大于0的股票。
A31:根据计算思路,计算每支股票公式一和公式二的仓位金额和现金余额。
A33:生成股票和仓位信息。
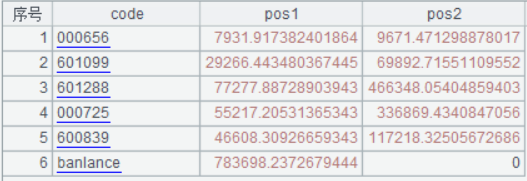
pos1可以看作低风险仓位,pos2可以看作高风险仓位,实战中可以根据个人偏好确定哪一种。



