7.4 层次 kmeans 聚类
有工业经验表明,重要度高的出料划分生产路线时所起的作用更大,为了体现这一作用,我们尝试了层次kmeans聚类,即按出料的重要度分层次进行kmeans聚类,过程如下:
1. 将所有出料数据X在初始化类心后用kmeans聚成2类,记录下类心。
2. 第1类数据不再参与聚类,对第2类数据用同样的方法聚成2类,并记录类心。
3. 按第2步的方法循环下去,直到类别数达到k或者只剩一个成员不能再聚类。
4. 预测时,每个预测数据Yi先和第1层类心计算距离,属于第1类就记录下来,属于第2类再和下一层的类心计算距离,确定是属于这一层的类别还是继续和下一层类心计算距离,如此循环,直到确认了Yi的类别为止。
SPL例程
A |
B |
C |
||
1 |
[[0.113,0.345,0.316], [0.118,0.314,0.322], [0.125,0.334,0.314], [0.139,0.254,0.371], [0.111,0.361,0.306], [0.179,0.257,0.332]] |
/X |
||
2 |
[[0.116,0.371,0.307], [0.143,0.324,0.303]] |
/Y |
||
3 |
=mk=3 |
|||
4 |
=center_seq=[] |
|||
5 |
=xc=A1.(0) |
|||
6 |
=idx_seq=to(A1.len()) |
|||
7 |
=col_seq=to(A1.~.len()) |
|||
8 |
=mstd@s(A1,1).~ |
|||
9 |
for |
=A1(idx_seq) |
/剩下的数据 |
|
10 |
=transpose(B9)(col_seq) |
|||
11 |
=A8(col_seq).psort@z() |
/Sidx |
||
12 |
=B10(B11) |
|||
13 |
=B12.(~.ranks()) |
/ RK的转置 |
||
14 |
=as=to(B13.len()),av_idx=to(B9.len()),B13.((oidx=as\#,pma=(~--msum(B13(oidx),1).~)(av_idx).pmax(),res=av_idx(pma),av_idx.delete(pma),res)) |
/Cb索引 |
||
15 |
=B9(B14.select(~)) |
/Cb’ |
||
16 |
=B15.to(2) |
/初始化类心C |
||
17 |
=k_means(B9,2,300,B16) |
|||
18 |
=B17(1) |
|||
19 |
=B17(2) |
|||
20 |
=B19.run(~=~+A9-1) |
|||
21 |
=B20.group@p(~) |
|||
22 |
=B21(1) |
|||
23 |
=B21(2) |
|||
24 |
=idx_seq(B22) |
|||
25 |
=idx_seq(B23) |
|||
26 |
=xc(B24)=B20(B22) |
|||
27 |
=idx_seq=B25 |
|||
28 |
=col_seq(B11.~) |
|||
29 |
=col_seq=col_seq\B28 |
|||
30 |
=center_seq.insert(0,[B18]) |
|||
31 |
if idx_seq.len()==1||A9==mk-1 |
=xc(B25)=B20(B23) |
||
32 |
break |
|||
33 |
=center_seq |
/类心集合 |
||
34 |
=yc=[] |
|||
35 |
=A33.len() |
|||
36 |
for A2 |
for A33 |
=B36.pmin(dis(~,A36)) |
|
37 |
=#B36 |
|||
38 |
=C36+C37-1 |
|||
39 |
if C36==1||C37==A35 |
=A34.insert(0,C38) |
||
40 |
next A36 |
|||
41 |
return [center_seq,xc,yc] |
|||
计算结果示例:
收率数据X:
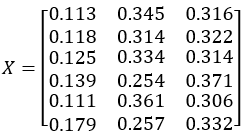
聚类数k=3。
预测数据Y:

第一层聚类类心C1:

第二层聚类类心C2:

X各成员所属类别Xc:
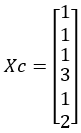
Y所属类别Yc:
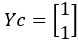
例程中的数据比较少,第2层聚类后,用来聚类的数据就只剩1个,无法继续分层了,所以即使把类别数k改成4甚至更大,聚类的结果还是只有3类。这是层次kmeans算法决定的,所以当需要聚成确定数量的离别时,还是要使用之前介绍的初始化类心的kmeans算法。



