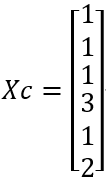kmeans的聚类结果受随机初始化的类心影响较大，有可能两次聚类的结果会因为初始类心的不同而不同，这会造成一种奇怪的现象，同一天的数据，因为两次聚类而属于两条生产路线，这是工业生产中不能接受的。

想要避免随机初始化类心的影响，需要输入一个确定的成员作为kmeans聚类的初始化类心，从而保证聚类结果稳定，可是这个初始化类心怎么选择呢？

生产路线是需要分的类，只要从收率数据中找到各生产路线下一个典型的成员，把这些典型成员作为初始类心传给kmeans算法即可。什么样的成员才是生产路线下的典型成员呢？

生产路线的特点是相应的出料收率较大，而其他收率较小。根据这一特点，可以把出料较大但其他收率和较小成员作为典型成员，应该怎么给生产路线排序呢？

需要一个量来衡量生产路线的重要程度，也就是需要一个量来衡量出料的重要程度。工业上会优先关注收率较大且波动较大的出料，根据这一特点，我们把出料收率的标准差定义为该出料的重要度，即某种出料的标准差越大，该出料越重要。

收率数据X中第j种出料的重要度ipt_j：

ipt_j=std(X_j)

根据上述思路，这样初始化类心C：

1. 计算各出料的重要度：

ipt_j=std(X_j)

其中，ipt_j是第j种出料的重要度。

按重要度倒序排序，并记录索引Sidx：

Sidx=[a_1, a_2,…, a_n],ipt_{a_1}>ipt_{a_2}>…>ipt_{a_n}

其中a_1, a_2,…, a_n是n种出料按重要度倒序排序后索引。

2. 收率数据转置后按出料重要度排序XT：

XT=X^T(Sidx)

其中，XT的每一行都是一种出料的收率，重要性从上到下递减。

3. 计算每种出料收率的排名RK_j，即收率越大，排名越靠后。

Rk_{a_j}=XT_{a_j}.ranks()

其中XT_{a_j}是第a_j种出料的收率，ranks()是排名方法。

排名矩阵RK：

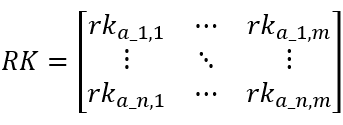
4. 找出备选类心Cb。

每种出料都可能对应一条生产路线，我们不妨把所有出料的典型成员都找出来作为备选类心Cb。

循环各出料收率，找出该出料排名减其他收率排名之和最大的点作为备选类心Cb_t。

Cb_t=X_h,h=pmax(rk_{a_ti}-sum([rk_{a_1i},rk _{a_2i},…,rk_{a_(t-1)i},rk_{a_(t+1)i},…,rk_ni])),i∈[1,2,…,m]\s,t∈[1,2,…,k]

其中Cb_t是第a_t个备选类心，也是第t个重要出料，h是X的第h行，也是RK的的第h列，pmax()是最大值索引方法，s是已经作为过类心的索引集合。

当出料很多时，可能会出现不同类别的初始类心是同一个点的情况，计算时要把已经作为类心的点去掉，即i∈[1,2,…,m]\s。

这里解释一下，为什么用收率的排名数据而不直接用收率的数值计算？

因为不同出料的收率数值差距可能比较大，比如柴油收率可能是0.3-0.5之间，而液化气收率可能只有0.05-0.1之间。它们的加减受数值的影响太大，无法准确找出生产路线下的典型成员，而用收率的排名计算则忽略了数值本身的影响，可以更准确的找出生产路线下的典型成员。

如果分类数k大于出料数n，则遍历所有点，找到距离已有备选类心距离和最远的点，将其加入到备选类心集合中，直到找到k个备选类心。

Cb_n+p=X_h,h=pmax(sum(dis(Cb_t,X_i))),p∈[1,2,…,k-n],t∈[1,2,…,n+p], i∈[1,2,…,m]

其中p是n个备选类心外的第p个。这里是一个循环的过程，每次循环的类心需要加入到原有的备选类心集合中，参与下次循环计算。

如果分类数k小于出料n，则只取重要性最高的k个备用类心最为最终的类心C。

Cb’=Cb(Sidx)

C=[Cb’₁, Cb’₂,…, Cb’_k]

其中，Cb’是Cb按出料重要性倒序排序后的类心，C是取Cb’的前k个成员。

SPL例程

计算结果示例：

收率数据X：

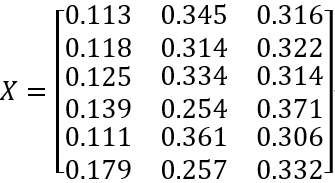
收率数据只是部分主要出料收率，所以收率和不为1，实际应用时也只是选择主要出料进行聚类。

聚类数k=3。

排名矩阵RK：

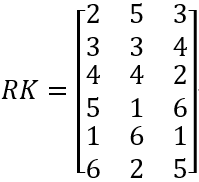
出料重要性IPT：

IPT=[0.0257, 0.0455, 0.0233]

IPT倒序排序后的索引Sidx:

Sidx=[2,1,3]

初始化类心C：

可以看到C₁的第2种出料收率是三个类心中最大的，C₂的第1种出料收率最大，C₃的第3种出料收率最大，最大值的索引[2,1,3]刚好对应Sidx。

kmeans聚类后的类心：

X各成员所属类别Xc：