工业上，某些装置的出料收率波动比较大，其中的一些出料量还需要特别关注，这些需要关注的出料往往与生产路线对应，比如催化装置中，汽油的收率大时，认为是汽油路线，柴油的收率大时，认为是柴油路线…现在希望把历史收率数据分成指定数量的类别，让它们对应到相应的生产路线，后续在建模（质量守恒约束下的线性模型）时，选择相同生产路线下的数据作为输入数据，从而提高模型的准确性。

某种进料不同出料的收率数据用X表示：

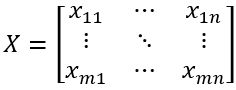
其中n是出料数，m是序号。每一行是某一天生产数据的不同出料的收率，每一列是某种出料每天的收率。

我们希望对收率数据X分类，但历史数据并没有标记好的分类数据，只能用无监督聚类，生产路线数对应分类数，kmeans聚类就可以满足聚类需求。

把收率数据X聚成的k类，聚类过程如下：

1. 随机选择k个数据作为初始类心C。

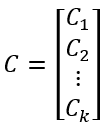
其中C_t是C的第t类的类心，是X中的某个随机成员。

2. 计算每个数据到这k个类心的距离，到哪个类心距离最近，就把该数据划为第k类。

xc_i=t,t=pmin(dis(X_i,C_t))

其中xc_i是X的第i行X_i的类别标记，C_t是第t类的类心，dis()是距离计算方法。

同一生产路线的收率相差不大，如果把X中的每一行看成高维空间中的一个点，同一生产路线下的点应该聚集在一起，不同生产路线的点又相对远离，所以我们选择欧式距离作为距离度量方法。

3. 更新类心。

计算每个类别中各种出料收率的均值，把它作为新的类心CN。

CN_t=avg(Xt_j),j∈[1,2,…,n],t∈[1,2,…,k]

其中CN_t是第t类的新类心，Xt_j是属于第t类的X的第j种出料收率。

4. 重复第2、3步，直到类心不在移动或达到最大迭代次数N。

即类心的距离和小于一个很小的数ε：

sum(dis(CN_t, CO_t))<ε|| iter==N,t∈[1,2,…,k]

其中CO_t是上次迭代类心的第t类的类心，ε是一个很小的数，iter是迭代的次数，dis()是距离计算方法。

迭代结束后，X中每个点到哪个类心C_t的距离最近就属于哪一类。

xc_i=t,t=pmin(dis(X_i,C_t))

SPL例程

计算结果示例：

输入数据X：

聚类数k=2

最大迭代次数iter=300

聚类结果：

类心C：

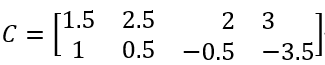
成员所属类别Xc：

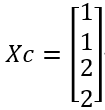
不难验证，X₁，X₂到C₁的距离近，它们的均值就是C₁，X₃，X₄到C₂的距离近，它们的均值就是C₂。