SPL 量化系列实践:KNN 简单策略
交易策略如下:
1. 把第二天是否上涨作为目标(target),收盘价大于前一天,target为1,否则target为-1。
2. 增加两个特征,最高价减最低价(max_dif),收盘价减开盘价(co_dif)。
3. 选择2023年的股价作为预测对象,计算当天的两个特征(max_dif和co_dif)与之前660个交易日的特征距离,找到距离最近的95个交易日,把这95个交易日的target的众数作为第二天涨跌的预测结果(predict),预测涨则为1,否则为-1。
4. 当predict=1且空仓时,下买入订单;predict=-1且有持仓股票时,下卖出订单。据此生成下单信号(flag),flag=1为买入,flag=-1为卖出,flag=0为不操作。
SPL代码
A |
|
1 |
=file("daily/300750.csv").import@tc() |
2 |
=A1.select(trade_date>20200101&&trade_date<=20231231) |
3 |
=A2.derive(if(#>1, close/ pre_close *factor[-1], close/pre_close):factor) |
4 |
=hfq_fst=A3(1),A3.derive((fcls=factor/hfq_fst.factor*hfq_fst.close,c=fcls/close,round(c*open,2)): hfq_open,round(c*high,2): hfq_high,round(c*low,2): hfq_low,round(fcls,2): hfq_close) |
5 |
=A4.derive(round(hfq_high-hfq_open,2):max_dif,round(hfq_close-hfq_open,2):co_dif,if(!hfq_close[1],,if(hfq_close[1]>hfq_close,1,-1)):target) |
6 |
=n=95 |
7 |
=ps=0 |
8 |
=A5.derive(if(trade_date<20230101,null,(train=~[-660,-1].([max_dif,co_dif]),rtarget=~[-660:-1].(target),v=[max_dif,co_dif],rtarget(train.ptop(n,dis(~,v))).mode())):predict,if(ps==0&&predict==1,(ps=1,1),if(ps!=0&&predict==-1,(ps=0,-1),0)):flag,if(flag!=0,100,0):shares) |
9 |
=A8.select(predict) |
A4:对股价进行复权,包括开、高、低、收。
A5:计算2个特征和目标变量。

A8:计算2023年的预测结果(predict),并根据预测结果和是否有仓位确定买卖信号(flag),每次买卖都是100股。

A9:筛选出predict不为null的数据。
SPL虽然没有提供现成的KNN算法,但实现起来并不复杂,只要一句话rtarget(train.ptop(n,dis(~,v)).mode()就能实现,像KNN这种简单的算法,SPL虽然要手动编码,但好在自由,能够根据需要设置参数和优化算法,而Python的第三方库是现成的算法库,参数设置有点烦,想要优化算法几乎不可能,还是要自己编码来完成。
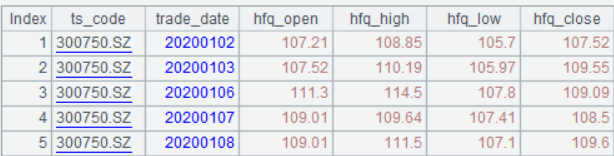
根据A9的数据画出买卖信号图:
红色圆点是买入点,绿色方点是卖出点。
和《海龟策略》一样,计算出flag后就可以回测了,过滤出A9数据中flag不为0的行,调用回测接口即可。
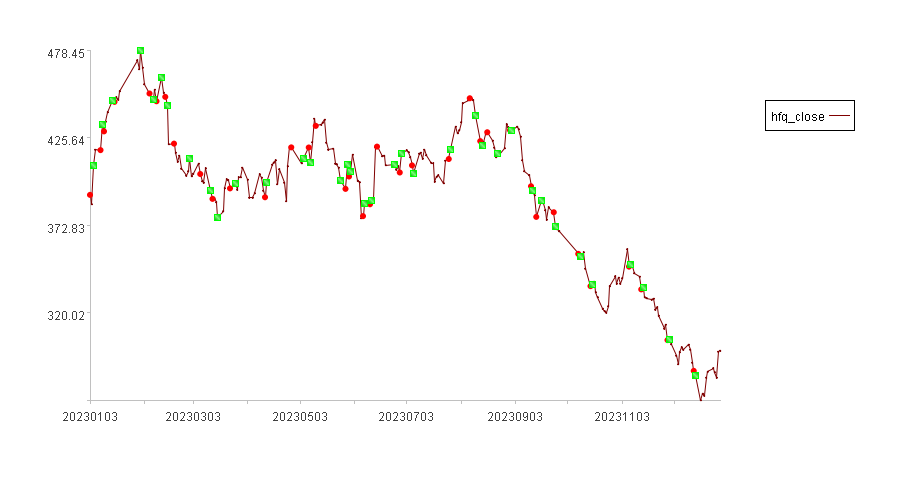
回测收益率图如下:
回测指标见下表:
indicators |
value |
累计收益率 (cumulative rate of return) |
5.54% |
年化收益率 (annualized rate of return) |
5.77% |
年化波动率 (annual volatility) |
15.59% |
夏普比率 (sharpe ratio) |
0.18 |
最大回撤 (maximum drawdown) |
14.63% |
投入现金 (cash invested) |
40425.29 |
总资产 (total assets) |
42664.29 |
仓位占比 (stock holding ratio) |
0.0% |
盈利次数 (profit times) |
18 |
亏损次数 (losses times) |
18 |
这里要说明一下,年化收益率是按每年252个交易日来算的,具体到某一年可能少几天也可能多几天,而且本例中第一次买入的时间是2023年1月20日,所以年化收益率和累计收益率不同。




英文版