程序设计习题 第 6 章 重复用
6.1 自定义函数
1. 编写一个计算整数立方用的函数，并计算1到10每个数和其前一个相邻整数的立方差。
例如2，前一个相邻数为1，两者的立方差等于7
2. 编写函数，把华氏温度转换为摄氏温度，公式为C=(F-32)*5/9，并调用函数计算73℉对应的摄氏温度。
3. 编写函数，利用边长计算三角形面积
给出三条边，判断是否可以组成三角形，如果可以的话计算面积
提示：利用边长计算三角形面积公式为海伦公式
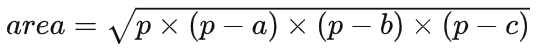，p为周长的一半
4. 自定义函数计算一个空心圆柱体的体积，输入外径R、内径r和高h，计算出体积。
提示：圆柱体的体积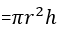
5. 自定一个计算BMI的函数，输入身高，体重，输出BMI
6. 一个数如果恰好等于它的所有因子之和，这个数就称为"完数"。例如6=1＋2＋3。
如何确定完数，欧几里发现，只要2n-1是一个素数，则2n-1（2n-1）一定一个完数（n>=2）。编写程序找出最小的5个完数。要求自定义函数判断2n-1是否是素数
7. 实现一个函数，可统计任一整数中某个数字出现的次数。例如-21252中，2出现了3次，则该函数应该返回3。
8. 求方程ax^2 + bx + c = 0的根。其中参数a,b,c是从main函数输入的。
6.2 递归
1. 编写一个递归函数，返回整数x和y的最大公约数
2. 猴子摘了一堆桃子，第一天吃了一半，觉得不过隐又吃了一个；第二天吃了剩下的一半零一个；以后每天如些，到第十天，猴子一看只剩下一个了。问最初有多少个桃子
3. 一只青蛙一次可以跳上1级台阶，也可以跳上2级。求该青蛙跳上一个n级的台阶总共有多少种跳法。
4. 用递归思想倒序输出一个正整数。例如给出正整数 n=12345，希望以各位数的逆序形式输出，即输出54321
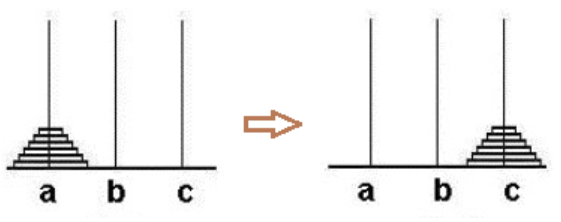
5. 汉诺塔问题： 给定三根柱子，记为a, b, c，其中a柱子上有n个盘子，且上面的盘子一定比下面的盘子小。问：将a柱上的盘子经由b柱移动到c柱最少需要多少次？
移动时应注意：
① 一次只能移动一个盘子
②大的盘子不能压在小盘子上
6.3 可复用脚本
1. 将利用边长计算三角形面积的方法编辑为可复用脚本，并调用
2. 将BMI的计算方法编辑为可复用脚本，并调用
参考答案：
6.1 自定义函数
1.
| A | B | |
| 1 | func | return A1*A1*A1 |
| 2 | =10.(func(A1,~)-func(A1,~[-1])) | |
2.
| A | B | |
| 1 | func | return (A1-32)*5/9 |
| 2 | =func(A1,73) | |
3.
| A | B | C | D | |
| 1 | func | |||
| 2 | if A1 + B1 > C1 && A1 + C1 > B1 && B1 + C1 > A1 | =A1+B1+C1 | =C2/2 | |
| 3 | =sqrt(D2*(D2-A1)*(D2-B1)*(D2-C1)) | |||
| 4 | return C3 | |||
| 5 | else | return "This side length group does not form a triangle" | ||
4.
| A | B | C | |
| 1 | func | ||
| 2 | return pi()*A1*A1*C1-pi()*B1*B1*C1 | ||
5.
| A | B | |
| 1 | func | |
| 2 | return B1/(A1*A1) | |
6.
| A | B | C | D | E | |
| 1 | 0 | 2 | |||
| 2 | for A1<5 | if func(A5,B1)==1 | >output(int(power(2,B1-1)*(power(2,B1)-1))) | >A1+=1 | |
| 3 | >B1+=1 | ||||
| 4 | |||||
| 5 | func | =power(2,A5)-1 | |||
| 6 | if A5==2 | return 1 | |||
| 7 | else | for 2,sqrt(B5) | if B5%C7==0 | return 0 | |
| 8 | break C7 | ||||
| 9 | return 1 | ||||
7.
| A | B | C | D | |
| 1 | func | 0 | ||
| 2 | if A1<0 | >A1=-A1 | ||
| 3 | if A1==0 && B1==0 | return 1 | ||
| 4 | for A1 | if A1%10==B1 | >C1+=1 | |
| 5 | >A1\=10 | |||
| 6 | return C1 | |||
| 7 | =func(A1,-21252,2) | |||
8.
| A | B | C | D | |
| 1 | func | |||
| 2 | if A1==0 | return -C1/B1 | ||
| 3 | else | =B1*B1-4*A1*C1 | ||
| 4 | if C3 >0 | return [(-B1+sqrt(C3))/(2*A1),(-B1-sqrt(C3))/(2*A1)] | ||
| 5 | else if C3==0 | return -B1/(2*A1) | ||
| 6 | else | return "There are no real roots" | ||
| 7 | =func(A1,3,8,5) | |||
6.2 递归
1.
| A | B | C | |
| 1 | func | ||
| 2 | if B1==0 | return A1 | |
| 3 | else | return func(A1,B1,A1%B1) | |
| 4 | =func(A1,54,63) | ||
2.
| A | B | C | |
| 1 | func | ||
| 2 | if A1==1 | return 1 | |
| 3 | return (func(A1,A1-1)+1)*2 | ||
| 4 | =func(A1,10) | ||
3.
| A | B | C | |
| 1 | func | ||
| 2 | if A1==1 | return 1 | |
| 3 | elseif A1==2 | return 2 | |
| 4 | else | return func(A1,A1-1)+func(A1,A1-2) | |
| 5 | =func(A1,9) | ||
4.
| A | B | C | |
| 1 | func | if A1<10 | return output(A1%10) |
| 2 | =output(A1%10) | ||
| 3 | return func(A1, A1\10),B2 | ||
| 4 | =func(A1,12345) | ||
递归思想：首先输出这个数的个位数，然后再输出前面数字的个位数，直到之前没数字。
5.
| A | B | C | |
| 1 | func | if A1==1 | return 1 |
| 2 | return 2*func(A1,A1-1)+1 | ||
| 3 | =func(A1,10) | ||
英文版