SPL 实践:高维二值向量查找
本次实践的目标是从大量的高维(比如 512 维)二值向量中找到与目标向量最相似的成员。二值向量即各维度取值均为 0 或 1 的向量,“相似”指在高维空间中距离近,而距离有很多种,如欧式距离,马氏距离,cos 相似度等等。其中 cos 相似度是业内最常用于衡量向量的相似程度的方法,cos 相似度越大,距离越近,两个向量越相似。
高维向量数据集上不能定义出和距离相关的序,也就无法像关系数据库那样建立有效的索引,这时候要找出距离最近的成员就只能全遍历,当数据量很大时,性能就会很差了。
业界通常会用专业的向量数据库来解决这个问题,向量数据库中内置了一些用于向量查找的 ANN 算法(Approximate Nearest Neighbor),可以在相当大的概率下快速找到与目标向量距离最近的成员(不能保证 100% 找到),而大多数应用场景中这种近似解已经可以满足需求了。
不过向量数据库非常复杂沉重,ANN 算法很多(不同的相似问题需要不同的 ANN 算法),算法本身的参数也很多,实践过程中,几乎不可能一次就选对 ANN 算法且把算法参数调好,需要反复实验,遇到 ANN 算法无法满足需求时,还要自己重新定义距离并调整算法等,这些对于向量数据库而言也“超纲”了。
SPL拥有灵活高效的计算能力,而且提供了丰富的计算函数,可以方便地进行这类问题的实践,与其研究、部署、安装、调试向量数据库,还不如用 SPL 实践一遍。
数据按位存储
二值向量可以按位存储,每个维度只占一个二进制位,存储量更小,计算时按位运算,效率会提高很多。
512维二值向量是 512 个二进制位,即 64 字节。在 SPL 中可以用长度为 8 的 long 类型的序列表示。
下面代码将一批 512 维的二值向量转换成 SPL 的 btx 文件存储。
A |
|
1 |
=directory@p("raw_data") |
2 |
=A1.(file(~).read@b()) |
3 |
=A2.(blob(~)) |
4 |
=A3.new(filename@n(A1(#)):name,~.bits():data) |
5 |
=file("longdata.btx").export@b(A4) |
raw_data是原始数据的储存目录,其中每个文件对应一个向量,文件名是向量的标识,文件长度为 512 个字节,每个字节对应一个维度,形式如下:

A1:列出目录下的文件名
A2:读取文件
A3:将每份数据转成长度为 512 的二值序列,形式如下:
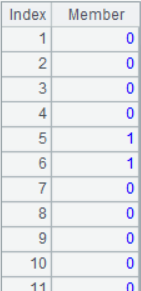
A4:创建序表,name 字段是向量的标识,即文件名,data 是 512 维二值序列转成的由 8 个 long 型整数构成的序列,形式如下:
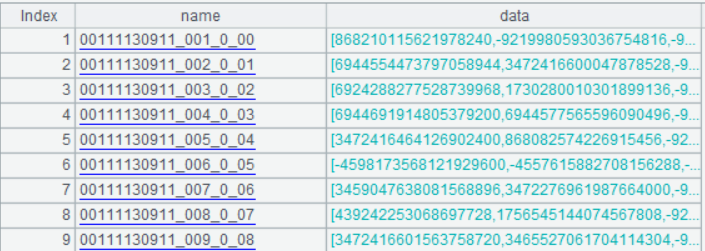
下面是第一行的 data 序列:
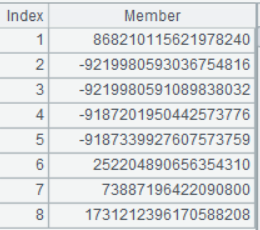
测试数据量 90 万行左右,转换后的longdata.btx 文件是一个 90 万行、2 列的二进制文件,大约 11M 大小。
把用于测试的待查找目标向量用同样的方式转换,生成”target_vec.btx”文件,方便后续比对。
用异或距离替代 cos 相似度
业界通常用 cos 相似度来衡量两个向量是否相似,但本例有点特殊,向量中的维度值非 0 即 1,cos 相似度会违反人的直观感受。比如:当 1 很多时,如果只有少量维度不同,算出的 cos 相似度会很大;当 0 很多时,还是少量维度不同时,算出的 cos 相似度会小很多。
比如 8 维向量:
x1=11111100
x2=11111010
x1,x2 只有两个维度不同,它们的 cos 相似度是 0.833。
x3=00000011
x4=00000101
x3,x4 也只有两个维度不同,它们的 cos 相似度却只有 0.5。
x1,x2 和 x3,x4 都只有两个维度不同,直观的感受是两组向量的相似度应该相同,但是 cos 相似度算出来的结果却相差很大。当维度更大时,这种差距会更大。
为了使结果更符合直观感受,我们使用异或距离来衡量向量相似度,异或距离是两向量对位不同的维度数。比如上例中 x1,x2 和 x3,x4 的异或距离都是 2,即两组向量的相似度相同。
SPL提供了 bit1() 函数,可以方便地算出两个序列的异或距离,下文中如无特别指出,距离均指异或距离。
SPL计算异或距离:
A |
||
1 |
=512.(rand(2)) |
/二值向量 1 |
2 |
=512.(rand(2)) |
/二值向量 2 |
3 |
=A1.bits() |
/long型数据序列 1 |
4 |
=A2.bits() |
/long型数据序列 2 |
5 |
=bit1(A3,A4) |
/异或距离 |
异或距离还有 1 个好处,相较于 cos 相似度,它只有位运算,没有除法运算,可以更快速地算出结果。
聚类尝试
ANN算法通常分为两部分:
1. 聚类,即把数据按照某种规则分到不同的子集,使这些子集内的点距离较近,同时使两个子集内的点距离较远,通俗点说就是把扎堆的数据分成一组, 同时使各堆尽量远。
2. 查询,查询目标向量的最相似向量时,只要遍历距目标向量最近的部分子集即可,不必遍历全部数据,这样做有时可能会找不到最近的成员,但大概率能找到,这是权衡准确率和查找效率的结果。
k-means是最常用的聚类方法,它要求事先确定类数k,这对于当前任务来讲是个难题,需要大量的尝试才能找到正确的k值;k-means 聚类过程中还要计算质心,而二值向量的质心不容易定义。综合考虑,k-means 算法对于当前问题并不太适用。
我们决定自行研发聚类方法,大概过程如下:
尝试将数据拆分成N个子集,每个子集的成员数阈值是M。
1. 所有数据是集合X,随机选 1 个向量作为第一个基向量x1,此时的集合也可以称作第一个子集X1。
2. 从X1中找到和基向量距离最远的向量,把它作为第二个子集X2的基向量x2。
3. 当有i个子集时,计算所有向量到每个基向量xi的距离,距离哪个基向量最近就将该向量划分到哪个子集。
4. 第i+1 个子集Xi+1的基向量xi+1是从已有的i个子集中找到成员数超过M且半径最大的子集中选择与其基向量最远的向量作为第i+1 个基向量xi+1。(子集的半径定义为子集中所有成员到其基向量的最远距离)
5. 重复第 3、4 步,直到所有子集成员数都小于M或子集数达到N。
计算距离(第 3 步的最近距离和第 4 步的最远距离)时会遇到距离相等的情况,这时可以加入随机数,让聚类更均匀一些。
完成聚类后,目标向量x’的比对过程如下:
1. 计算x’与所有基向量xi的距离,并按距离排序,取前K个最近子集。
2. 遍历K个子集的成员,计算他们与x’的距离,找到最近距离成员。
K的取值需要权衡计算效率和比对精度,K较小时,遍历量很少,计算很快,但找到最近距离成员的可能性也会小;调大K后,遍历量会增多,计算变慢,但找到最近成员的可能性会增大。
经过一些数学上的分析和实验测算,我们将K取为维度数或 2 倍维度数(每个维度有一个或两个方向寻找),并令M=10*sqrt( 数据量 / 维度数),N=20* 数据量 /M。
下面是用 SPL 实现的聚类过程:
A |
B |
C |
|
1 |
longdata.btx |
||
2 |
=s_no=600 |
||
3 |
=sub_no_thd=30000 |
||
4 |
=rad_thd=100 |
||
5 |
=file(A1).import@b() |
||
6 |
=X=A5.run(data=data.i()).i() |
||
7 |
=G=create(base,num,rad) |
||
8 |
=x1=X.maxp(data.sum(bit1(~))).data |
||
9 |
=X.len() |
||
10 |
=A8.len()*64 |
||
11 |
=G.record([A8,A9,A10]) |
||
12 |
=X.derive@o(1:grp,bit1(data,x1):dis,:new_dis,:flag) |
||
13 |
for |
||
14 |
=G.count(rad==0) |
||
15 |
=G.max(num) |
||
16 |
=G.max(rad) |
||
17 |
if G.len()>=sub_no_thd||B15<=s_no||B16<=rad_thd |
break |
|
18 |
=x1=X.groups@m(;maxp(if(G(grp).num>s_no||G(grp).rad>rad_thd, dis+rand(), 0)):mx).mx.data |
||
19 |
=G.record([x1]) |
||
20 |
=G.len() |
||
21 |
=X.run@m(bit1(data,x1):new_dis,new_dis-dis<2*rand()-1:flag,if(flag,new_dis,dis):dis,if(flag,B20,grp):grp) |
||
22 |
=X.groups@nm(grp;count(1):cnt,max(dis):rad) |
||
23 |
=G.run@nm(B22(#).cnt:num,B22(#).rad:rad) |
||
24 |
=X.new(A5(#).name:name,data,grp,dis).o() |
||
25 |
=A24.group(grp) |
||
26 |
=A25.align@a([false,true],~.len()==1) |
||
27 |
=A26(2).conj().new(name,data,int(grp):grp) |
||
28 |
=A27.len() |
||
29 |
=A26(1).conj().group([grp,dis]).conj().new(name,data,int(grp):grp) |
||
30 |
=file("indexes_1.btx").export@b(A27) |
||
31 |
=file("indexes_m.btx").export@b(A29) |
||
A6、A7:设置两个变量 X 和 G,分别存储每个向量的信息和聚类子集的信息。
A12:新增每个向量需要的信息,grp 是所属子集号,dis 是该向量到所属子集基向量的距离,new_dis 是循环过程中,有新基向量时,存储该向量到新基向量的距离,flag 是判断该向量属于新子集还是旧子集的标志。、
A13代码块:按照上述算法思路聚类的过程。
A24-A29:整理聚类结果,先按 grp 分组,把 1 个成员的子集和多成员子集单独存储,再按 [grp,dis] 分组,每个子集的第一个向量是基向量,方便后续查询,最后将其存储为二进制文件。
代码中的输入文件是二值向量转换后的 longdata.btx。
聚类完成后,输出两个文件,分别是 1 个成员子集数据 "indexes_1.btx" 和多成员子集数据 "indexes_m.btx",两者的数据结构相同,形式如下:
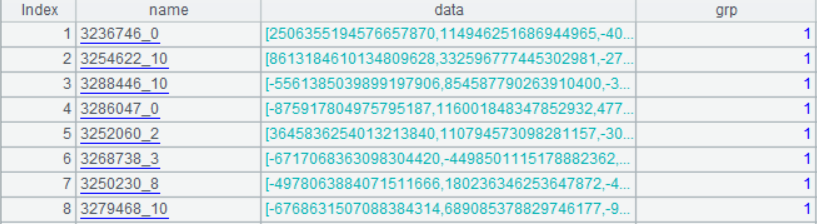
下面是用 SPL 实现的比对过程:
A |
B |
|
1 |
=file("target_vec.btx").import@b().run(data=data.i()).i() |
|
2 |
=sub_no=512 |
|
3 |
=X1=file("indexes_1.btx").import@b().run(data=data.i()).i() |
|
4 |
=X=file("indexes_m.btx").import@b().run(data=data.i()).i() |
|
5 |
=XG=A4.group@v0(grp).(~.run(data=data.i()).i()) |
|
6 |
=A5.(~(1)).run(data=data.i()).i() |
|
7 |
=(A3|A4).i() |
|
8 |
=ath_data_num=0 |
|
9 |
=ath_time=0 |
|
10 |
=all_time=0 |
|
11 |
=miss_bit=0 |
|
12 |
for A1 |
=xx=A12.data.i() |
13 |
=now() |
|
14 |
=A6.ptop(sub_no;bit1(xx,data)) |
|
15 |
=XG(B14) |
|
16 |
=B15.conj@v() |
|
17 |
=B16|X1 |
|
18 |
=B17.minp(bit1(xx,data)) |
|
19 |
=interval@ms(B13,now()) |
|
20 |
=now() |
|
21 |
=A7.minp(bit1(data,xx)) |
|
22 |
=interval@ms(B20,now()) |
|
23 |
=B18.(bit1(data,xx)) |
|
24 |
=B21.(bit1(data,xx)) |
|
25 |
=ath_data_num+=B17.len()+A6.len() |
|
26 |
=ath_time+=B19 |
|
27 |
=all_time+=B22 |
|
28 |
=if(B23!=B24,1,0) |
|
29 |
=miss_bit+=B28 |
|
30 |
=A1.len() |
|
31 |
=ath_data_num/A30 |
|
32 |
=ath_time/A30 |
|
33 |
=all_time/A30 |
|
34 |
=miss_bit/A30 |
|
35 |
=file("target_vec.btx").import@b().run(data=data.i()).i() |
|
36 |
=sub_no=512 |
|
A1:读入目标向量数据;
A3:读入 1 个成员的子集数据;
A4:读入多成员的子集数据;
A5:将多成员集合按 grp 分组;
A6:A5 中每个子集的第一个成员是基向量;
A12代码块:每个目标向量的比对过程;
B14:选出距离最近的K个子集;
B18:算出最近距离成员;
B21:全遍历最近距离成员。
变量 ath_data_num、ath_time、all_time、miss_hit 分别统计算法遍历数据量、算法耗时、全遍历耗时和算法最近距离不等于全遍历最近距离的次数。
A33-A36是上述统计量的平均值。
我们把算法找出的最近距离不等于全遍历计算出来最近距离的次数占全部目标向量数的比例(A36 的结果)叫做击不中率,作为算法有效性的考虑指标,显然击不中率越低说明这个算法有效性更高。
下面是 1 万个目标向量在聚类输出文件 "indexes_1.btx" 和 "indexes_m.btx" 上的统计结果:
数据量 |
遍历子集数 |
算法遍历数据量 |
算法耗时 |
全遍历耗时 |
击不中率 |
90万 |
512 |
80683 |
2.02ms |
18.15ms |
5.68% |
1024 |
114384 |
3.92ms |
17.48ms |
2.46% |
数学分析表明,这个算法的理论复杂度和数据量的平方根成正比,数千万数据量的耗时不超过 100ms, 比如数据量扩大到 9000 万,相当于 90 万的 100 倍,算法耗时只扩大到原来的 10 倍,遍历 512 个子集时耗时在 20ms 左右,遍历 1024 个子集时耗时在 40ms 左右,而全遍历耗时会扩大 100 倍,需要 1800ms 左右。
逐步聚类
上述的聚类方法是将整个集合拆分,形成一个个子集,我们把这种方法叫做拆分式聚类。它有一个弊端,数据拆分经常不彻底,即还没有把所有子集都拆成小于阈值M时,子集数已经到达阈值N了,这样很容易造成各子集成员数分布非常不均匀,即有的子集很大,而很多子集只有 1 个成员。
有鉴于此,我们又设计了逐步聚类的方法,过程如下:
设子集成员数阈值为M
1. 第一个基向量是第一个向量,记为x1,第一个子集记为X1。
2. 遍历整个集合X,把X的成员加到最近的子集Xi中(距离相等时,随机加)。
3. 加到有Xi的成员数超过M时,对遍历过的数据拆分,使所有Xi成员数都小于等于M(拆分过程就是拆分式聚类过程)。
4. 循环 2,3,直到X遍历完。为了避免拆分式聚类无限进行,按遍历过的数据量动态计算子集数阈值M’=sqrt(遍历过的数据量 *1024),M’是遍历过的数据量的子集数阈值,这样做可以保证后面的数据总有机会作为基向量。)
相较于拆分式聚类,逐步聚类的方式可以使聚类更彻底,最终的子集数通常小于拆分式聚类。
SPL逐步聚类代码:
A |
B |
C |
D |
E |
|
1 |
longdata.btx |
||||
2 |
=s_no=600 |
||||
3 |
=file(A1).import@b() |
||||
4 |
=to(A3.len()).psort(rand()) |
||||
5 |
=X=A3(A4).new(data).run(data=data.i()).derive@o(:grp,:dis,:new_dis,:flag).i() |
||||
6 |
=G=create(base,num,rad,max_rad_v) |
||||
7 |
=x1=X.data |
||||
8 |
=G.record([A7,0,0,null]) |
||||
9 |
for X |
=xid=#A9 |
|||
10 |
=sub_num_step=sqrt(xid*1024) |
||||
11 |
=v0=A9.data |
||||
12 |
=G.@m(bit1(base,v0)) |
||||
13 |
=B12.pmin(~+rand()) |
||||
14 |
=B12(B13) |
||||
15 |
=G(B13).run(num=num+1,(dst=B14,flg=dst+rand()>rad+rand(),rad=if(flg,dst,rad)),max_rad_v=if(flg,v0,max_rad_v)) |
||||
16 |
=A9.run(B13:grp,B14:dis) |
||||
17 |
=G(B13).num |
||||
18 |
=G.len() |
||||
19 |
if B18>sub_num_step |
next |
|||
20 |
if B17>s_no |
=X(to(#A9)) |
|||
21 |
for |
=G.len() |
|||
22 |
if D21>sub_num_step |
break |
|||
23 |
=G.groups@m(;maxp(if(num<=s_no||rad==0,-1,rad+rand())):mx).mx |
||||
24 |
if D23.num>s_no |
=x1=D23.max_rad_v |
|||
25 |
else |
break |
|||
26 |
=G.record([x1]) |
||||
27 |
=C20.run@m(bit1(data,x1):new_dis,new_dis-dis<2*rand()-1:flag,if(flag,new_dis,dis):dis,if(flag,D21+1,grp):grp) |
||||
28 |
=D27.groups@nm(grp;count(1):cnt,max(dis):rad,maxp(dis).data:max_rad_v) |
||||
29 |
=G.run@m((rcd=D28(#),num=rcd.cnt,rad=rcd.rad,max_rad_v=rcd.max_rad_v)) |
||||
30 |
=A3(A4).derive(X(#).grp:grp,X(#).dis,G(grp).rad:rad) |
||||
31 |
=A30.group(grp) |
||||
32 |
=A31.align@a([false,true],~.len()==1) |
||||
33 |
=A32(2).conj().run(grp=int(grp)).derive(int(#):ID) |
||||
34 |
=A33.len() |
||||
35 |
=A32(1).conj().group([grp,dis]).conj().run(grp=int(grp)).derive(int(A34+#):ID) |
||||
36 |
=file("indexes2_1.btx").export@b(A33) |
||||
37 |
=file("indexes2_m.btx").export@b(A35) |
||||
算法的输入和输出和拆分式聚类类似,只是名字不同。
A4:将数据随机排序;
A9代码块:逐步聚类过程;
C21代码块:拆分式聚类过程。
查询过程和之前相同,这里不再赘述。
下面是同样数据逐步聚类的实验结果:
数据量 |
遍历子集数 |
算法遍历数据量 |
算法耗时 |
全遍历耗时 |
击不中率 |
90万 |
512 |
81212 |
2.33ms |
16.63ms |
2.43% |
1024 |
128311 |
4.37ms |
17.20ms |
0.82% |
效果比拆分式聚类更好一些。
交集方法
遍历 512 个子集的击不中率为 2.43%,还是有点高。
逐步聚类是随机打乱所有数据顺序后再聚类,聚类过程中距离相等时也会随机处理,可能会产生随机性较强的聚类结果。我们可以利用聚类的随机性,多次聚类后,取两者击不中的交集,减少击不中率。
具体做法如下:
1. 按原来的比对方法找到每次随机聚类的最近距离成员;
2. 再从两个最近距离成员中选出距离更近的成员(相当于取两次结果的击不中成员的交集)。
下面是用 SPL 实现的交集方法:
A |
B |
C |
|
1 |
=file("target_vec.btx").import@b().run(data=data.i()).i() |
||
2 |
=sub_no=1024 |
||
3 |
indexes2_1_1.btx |
||
4 |
indexes2_1_2.btx |
||
5 |
indexes2_m_1.btx |
||
6 |
indexes2_m_2.btx |
||
7 |
=[A3:A6].(file(~).import@b(name,data,grp).run(data=data.i()).i()) |
||
8 |
=A7.to(2) |
||
9 |
=A7.to(3,) |
||
10 |
=A7.to(3,).(~.group@v0(grp).(~.run(data=data.i()).i())) |
||
11 |
=A10.(~.(~(1)).run(data=data.i()).i()) |
||
12 |
=(A7(1)|A7(3)) |
||
13 |
=ath_data_num=0 |
||
14 |
=ath_time=0 |
||
15 |
=all_time=0 |
||
16 |
=miss_hit=0 |
||
17 |
for A1 |
=xx=A17.data.i() |
|
18 |
=s=0 |
||
19 |
=now() |
||
20 |
for 2 |
||
21 |
=X1=A8(B20) |
||
22 |
=X=A9(B20) |
||
23 |
=XG=A10(B20) |
||
24 |
=A11(B20) |
||
25 |
=C24.ptop(sub_no;bit1(xx,data)) |
||
26 |
=XG(C25) |
||
27 |
=C26.conj@v() |
||
28 |
=C27|X1 |
||
29 |
=s+=C28.len()+C24.len() |
||
30 |
=C28.minp(bit1(xx,data)) |
||
31 |
=@|C30 |
||
32 |
=C31.minp(bit1(xx,data)) |
||
33 |
=interval@ms(B19,now()) |
||
34 |
=C31=[] |
||
35 |
=now() |
||
36 |
=A12.minp(bit1(data,xx)) |
||
37 |
=interval@ms(B35,now()) |
||
38 |
=B32.(bit1(data,xx)) |
||
39 |
=B36.(bit1(data,xx)) |
||
40 |
=if(B38!=B39,1,0) |
||
41 |
=ath_time+=B33 |
||
42 |
=all_time+=B37 |
||
43 |
=miss_hit+=B40 |
||
44 |
=ath_data_num+=s |
||
45 |
=A1.len() |
||
46 |
=ath_time/A45 |
||
47 |
=all_time/A45 |
||
48 |
=miss_hit/A45 |
||
49 |
=ath_data_num/A45 |
||
B20代码块:两次次聚类结果的比对过程。
两次聚类后,查询时也要比对两次,遍历数据量是两次比对的遍历数据量之和,这会增加比对耗时,但能大幅降低了击不中率。
以下是逐步聚类随机聚类两次的实验结果:
遍历子集数 |
遍历数据量 |
算法耗时 |
全遍历耗时 |
击不中率 |
512 |
163771 |
6.16ms |
16.62ms |
0.18% |
1024 |
260452 |
9.34ms |
17.11ms |
0.06% |
维度排序
除了减少遍历量的方式可以减少计算量外,还可以通过减少维度数来减少计算量,假如某个维度上全是 0(或 1),则该维度对距离的贡献永远是 0,也可以说该维度对于距离计算的敏感度是 0,显然没有计算的必要。类比地考虑,如果某个维度绝大部分是 0(或 1),则它在距离上的贡献会比 0 和 1 数量接近的维度要小很多,也就是敏感度更低。我们优先计算敏感度更高的维度,敏感度过低的维度不再计算,这样能更充分地利用有限的计算资源。
维度的敏感度定义为:
1-abs(数据集在该维度上 1 的数量 / 数据量 -0.5)
我们将所有维度按敏感度排序,只使用前一部分维度来减少计算量。在数据准备阶段,将维度排序后再把二值序列转换成 long 型数据。
重新改造最初的数据转换程序:
A |
B |
C |
|
1 |
=directory@p("raw_data") |
||
2 |
=512*[0] |
||
3 |
=A1.run(A2=A2++blob(file(~).read@b())) |
||
=A1.len() |
|||
5 |
=A2.psort(abs(~/A4-0.5)) |
||
6 |
=func(A12,A1,A5) |
||
7 |
=directory@p("x0_data") |
||
8 |
=func(A12,A7,A5) |
||
9 |
=file("longdata1.btx").export@b(A6) |
||
10 |
=file("div_index1.btx").export@b(A5) |
||
11 |
=file("target_vec1.btx").export@b(A8) |
||
12 |
func |
||
13 |
=A12.group((#-1)\100000) |
||
14 |
=A12.len() |
||
15 |
=create(name,data) |
||
16 |
for B13 |
=B16.(blob(file(~).read@b())(B12).bits()) |
|
17 |
=B16.(filename@n(~)) |
||
18 |
=C17.(~|[C16(#)]).conj() |
||
19 |
=B15.record(C18) |
||
20 |
return B15 |
||
A3:统计各维度 1 的个数;
A5:按 (1- 敏感度) 排序;
A6:转换所有数据;
A8:转换目标数据;
A12代码块:将二值数据排序并转换成 long 型数据;
聚类过程和原来类似,区别只是用前部分敏感度高的维度(比如前p个 long 型数据,也就是前p*64 个维度)来聚类。
比对过程也差不多,有以下几点区别:
1. 目标向量要按敏感度排序后再转换成 long 型数据,同样取前p个 long 型数据;
2. 按原来的方式从前p个 long 型数据选出距离最近的topn个向量,因为只计算前p个 long 的距离,无法确定前p个 long 的最近距离成员一定是全维度最近距离成员,所以取前topn个向量,使其大概率包含全维度最近距离成员,结合交集方法,可以进一步增加这一概率;
3. 计算这topn个向量的全维度距离,找到最近距离成员;
4. 用交集方法降低击不中率。
经过实验,当p=5 时(前 320 个维度),可以获得不错的击不中率。
下面是用 SPL 代码实现的比对过程:
A |
B |
C |
|
1 |
=pre_n_long=5 |
||
2 |
=topn=50 |
||
3 |
=sub_no=1024 |
||
4 |
indexes3_1_1.btx |
||
5 |
indexes3_1_2.btx |
||
6 |
indexes3_m_1.btx |
||
7 |
indexes3_m_2.btx |
||
8 |
=[A4:A7].(file(~).import@b(name,data,grp).derive(data.to(pre_n_long):data1).run(data=data.i(),data1=data1.i()).i()) |
||
9 |
=A8.to(2) |
||
10 |
=A8.to(3,) |
||
11 |
=A8.to(3,).(~.group@v0(grp).(~.run(data=data.i(),data1=data1.i()).i())) |
||
12 |
=A11.(~.(~(1)).run(data=data.i(),data1=data1.i()).i()) |
||
13 |
=(A8(1)|A8(3)) |
||
14 |
=ath_data_num=0 |
||
15 |
=ath_time=0 |
||
16 |
=all_time=0 |
||
17 |
=miss_hit=0 |
||
18 |
=file("target_vec1.btx").import@b() |
||
19 |
for A18 |
=xx=A19.data.i() |
|
20 |
=xx.to(pre_n_long) |
||
21 |
=s=0 |
||
22 |
=now() |
||
23 |
for 2 |
||
24 |
=X1=A9(B23) |
||
25 |
=X=A10(B23) |
||
26 |
=XG=A11(B23) |
||
27 |
=A12(B23) |
||
28 |
=C27.ptop(sub_no;bit1(B20,data1)) |
||
29 |
=XG(C28) |
||
30 |
=C29.conj@v() |
||
31 |
=C30|X1 |
||
32 |
=s+=C31.len()+C27.len() |
||
33 |
=C31.top(topn;bit1(B20,data1)) |
||
34 |
=C33.minp(bit1(xx,data)) |
||
35 |
=@|C34 |
||
36 |
=C35.minp(bit1(xx,data)) |
||
37 |
=interval@ms(B22,now()) |
||
38 |
=C35=[] |
||
39 |
=now() |
||
40 |
=A13.minp(bit1(data,xx)) |
||
41 |
=interval@ms(B39,now()) |
||
42 |
=B36.(bit1(data,xx)) |
||
43 |
=B40.(bit1(data,xx)) |
||
44 |
=ath_time+=B37 |
||
45 |
=all_time+=B41 |
||
46 |
=if(B42!=B43,1,0) |
||
47 |
=miss_hit+=B46 |
||
48 |
=ath_data_num+=s |
||
49 |
=A18.len() |
||
50 |
=ath_time/A50 |
||
51 |
=all_time/A50 |
||
52 |
=miss_hit/A50 |
||
53 |
=ath_data_num/A49 |
||
B23代码块:比对过程;
C34:全维度最近距离;
维度排序减少了横向计算量,聚类也提速不少。
下面是 90 万数据综合采用逐步聚类、交集方法、维度排序的比对结果:
数据量 |
遍历子集数 |
遍历数据量 |
算法耗时 |
全遍历耗时 |
击不中率 |
90万 |
512 |
159381 |
5.60ms |
17.46ms |
0.68% |
算法性能约有 10% 的提升。




英文版