北京
润乾公司大数据计算专家
2 回帖  •  928 浏览  • 
     ...

SPL 计算性能系列测试：位置关联

 
二分法(2) 集算器(484) SQL困难(18) 性能优化(158) 解决方案(56) 列式计算(1)

一、 测试任务

基于位置计算两个实体之间的距离，进而决定是否建立关联关系。这是典型的非等值关联运算，此时不能再使用 HASH 方法来优化。

任务原型来自国家天文台的星体聚类运算，经过简化后描述如下：

一张天体照片中有 n 个天体，每个天体有各种属性，一个天体及其属性为一条记录，一张照片中的所有天体及其属性组成一张表。

现有两张照片的数据，分别存储在表 A 和表 B 中，表结构一样，如下：

列名

数据类型

说明

SN

int

序号，从 0 开始

InputMAGG

decimal

天体的属性，最后需要把认定为同一个天体的所有记录的此属性值汇总求平均值

OnOrbitRA

decimal

天体位置坐标里的赤经

OnOrbitDec

decimal

天体位置坐标里的赤纬

生成结果表的结构：

列名

数据类型

说明

SN

int

匹配上的天体为第一张表的 SN，没匹配上的天体为该天体的 SN

CNT

int

匹配上的天体个数，没匹配上则为 1

SN_COM

varchar

匹配上的天体的 SN，用下划线连接成字符串，未匹配上的天体填 null

InputMAGG

decimal

匹配上天体的InputMAGG平均值，未匹配上的天体则填自己的InputMAGG

OnOrbitRA

decimal

匹配上天体的OnOrbitRA平均值，未匹配上的天体则填自己的OnOrbitRA

OnOrbitDec

decimal

匹配上天体的OnOrbitDec平均值，未匹配上的天体则填自己的OnOrbitDec

计算 A 照片中的天体和 B 照片中天体的距离，如果小于某个阈值，则认定这两个天体为同一个，然后按照上述要求生成结果表。

SN 是天体的编号，A、B 表中的 SN 都是从小到大有序且唯一。对于 A 表的某条记录，从 B 表的第一条记录开始遍历，一旦找到认定为同一个天体的记录（距离小于阈值）后，后面的就不再遍历了，即 B 表中满足同一条 A 表记录距离条件的所有记录中 SN 值最小的记录才被认定为与 A 表相应记录是同一个天体。

当 B 中的某条记录被 A 中的某条记录认定为同一个天体后，开始计算 A 中下一个天体时，曾经被匹配上的记录不再参与计算。即 B 表中的记录最多只能被匹配一次。

A、B 表中未被匹配上的记录，也合并到结果表中，SN_COM 字段值为空，表示没有匹配的天体，CNT 字段值为 1，表示只有自己一个天体。

天体的距离

天体（object）在天球上的位置坐标由（ra,dec）表示，其中ra为赤经，dec为赤纬（可类比地球的经度、纬度）。

如果object1在天球上的位置为（ra1,dec1），object2的位置为（ra2,dec2），他们之间的距离dis这样计算：

..

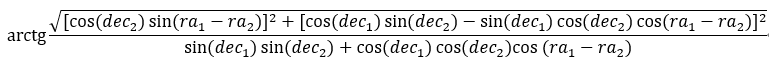
天体的匹配条件即是计算出来的dis<=D，D是指定的参数，在这里用0.3/3600。

上述公式中的dec和ra分别对应表结构中的OnOrbitDec和OnOrbitRa。

初筛 delta

上述计算式较为复杂，计算量较大。

可以从数学上证明如下结论，如果上式满足时，必然有：

..

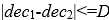
且存在某个delta，使得：

..

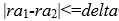
这样可以用这个简单的条件做初筛，不满足此条件的，必然不会满足上面的复杂条件。

其中的delta 计算方法如下：

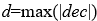..，即数据中所有dec的绝对值的最大值

..

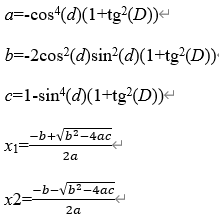
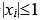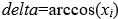若有某个..时，则..，两个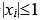.. 时，任取一个就可以

若两个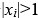..，则..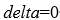

二．对比技术

我们选择了下面两种数据库产品用为对比技术：

1、Starrocks, 宣称最快的 SQL 数据仓库，测试版本 3.0

2、Oracle，使用量很大，常常作为数据库性能测试的对比标杆，测试版本 19

目前 SPL 尚未提供针对三角函数的向量式计算，企业版并不会有明显优势，因此只测了社区版，版本是 20230528。

三．测试环境和数据

单台物理服务器，配置：

2 颗 Intel3014，主频 1.7G，共 12 核 CPU

64G 内存

SSD 固态硬盘

虚拟机配置：

操作系统：Red Hat 4.8.5-44

VM1：8CPU，32G 内存

VM2：4CPU，16G 内存

当前应用大多数会跑在虚拟机上，因此我们在这里直接在虚拟机上测试，考查被测技术在虚拟机上的表现以及 CPU 核数和内存的敏感性。根据业界较常见的云虚拟机规格，我们设计了上述两套虚拟机测试环境 VM1 和 VM2。

Starrocks 至少要安装两个节点 BE 和 FE，将承担计算任务的 BE 安装在虚拟机上，管理节点 FE 安装在物理机上，这样不会影响测试效果。SPL 和 Oracle 都只要在虚拟机下安装就可以了。

测试的数据量规模分三种：A、B 表各 1 万行、10 万行、50 万行，以下为供下载的数据压缩包

data.zip

四．SQL 测试 (Starrocks)

SQL 的逻辑说明：

1、将 A、B 表中的 OnOrbitRA 和 OnOrbitDec 从角度转成弧度，并提前算好其 sin 值和 cos

2、将 A、B 表关联，关联条件为前述的满足距离 dis<=D，并同时使用了初筛，即 |dec1-dec2|<=D 和 |ra1-ra2|<=delta

3、SQL 中的 1.6548341646645552E-6 就是提前算好的 delta

4、然后按照 A 表的 SN 分组，每组中的记录按 B 表的 SN 排序，算出记录序号，筛选出序号为 1 的记录，即为匹配上的天体

5、最后按照要求，将满足匹配条件的天体算出 OnOrbitRA、OnOrbitDec 和 InputMAGG 的平均值，将 SN 用 _ 拼接起来作为 SN_COM 的值，将匹配的天体个数存在 CNT 字段中。

6、没有匹配上的 A、B 表中的记录，将 SN_COM 置为空，CNT 置为 1，合并到结果集中

WITH A AS(
	SELECT SN,
		OnOrbitRA,
		OnOrbitDec,
		InputMAGG,
		PI()/180*OnOrbitRA RA,
		PI()/180*OnOrbitDec aDEC,
		SIN(PI()/180*OnOrbitDec) SIN_DEC,
		COS(PI()/180*OnOrbitDec) COS_DEC 
	FROM A
	),
B AS(
	SELECT SN,
		OnOrbitRA,
		OnOrbitDec,
		InputMAGG,
		PI()/180*OnOrbitRA RA,
		PI()/180*OnOrbitDec aDEC,
		SIN(PI()/180*OnOrbitDec) SIN_DEC,
		COS(PI()/180*OnOrbitDec) COS_DEC 
	FROM B
	),
T0 AS (
	SELECT A.SN A_SN,B.SN B_SN, 
		B.OnOrbitRA B_OnOrbitRA,B.OnOrbitDec B_OnOrbitDec,B.InputMAGG B_InputMAGG, 
		A.OnOrbitRA A_OnOrbitRA,A.OnOrbitDec A_OnOrbitDec,A.InputMAGG A_InputMAGG 
	FROM A JOIN B 
		ON A.OnOrbitDec>=B.OnOrbitDec-0.5/3600 
			and A.OnOrbitDec<=B.OnOrbitDec+0.5/3600 
			and A.RA>=B.RA-1.6548341646645552E-6 
			and A.RA<=B.RA+1.6548341646645552E-6 
			and (SQRT(POWER(B.COS_DEC*SIN(A.RA-B.RA),2)
				+POWER(A.COS_DEC*B.SIN_DEC-A.SIN_DEC*B.COS_DEC*COS(A.RA-B.RA),2))
				/(A.SIN_DEC*B.SIN_DEC+A.COS_DEC*B.COS_DEC*COS(A.RA-B.RA)))
				<=TAN((PI()/180)*(0.3/3600))
	),
T1 AS (
	SELECT *,ROW_NUMBER() OVER ( PARTITION BY B_SN ORDER BY A_SN ) RN 
	FROM T0
	), 
T2 AS (
	SELECT * FROM T1 WHERE RN=1
	),
T3 AS (
	SELECT A_SN SN, 
		1+COUNT(*) CNT, 
		CONCAT(CAST(A_SN AS VARCHAR(1000)), '_', GROUP_CONCAT(CAST(B_SN AS VARCHAR(1000)),'_')) SN_COM,
		(A_OnOrbitRA+SUM(B_OnOrbitRA))/(COUNT(*)+1) OnOrbitRA,
		(A_OnOrbitDec+SUM(B_OnOrbitDec))/(COUNT(*)+1) OnOrbitDec,
		(A_InputMAGG+SUM(B_InputMAGG))/(COUNT(*)+1) InputMAGG 
	FROM T2 
	GROUP BY A_SN,A_OnOrbitRA,A_OnOrbitDec,A_InputMAGG
	)
SELECT * FROM T3
UNION ALL 
	SELECT SN, 1 CNT, NULL SN_COM, OnOrbitRA, OnOrbitDec, InputMAGG 
	FROM A 
	WHERE NOT SN IN ( SELECT A_SN FROM T1 ) 
UNION ALL 
	SELECT SN, 1 CNT, NULL SN_COM, OnOrbitRA, OnOrbitDec, InputMAGG 
	FROM B 
	WHERE NOT SN IN ( SELECT B_SN FROM T1 );

五．SQL 测试 (Oracle)

Oracle 的 SQL 逻辑和 Starrocks 一样，只是语法不同，有如下几处改动点：

1、 用 ACOS(-1) 代替 PI()

2、 临时表名不能和实际表名一样，所以临时表名改成了 A1，B1

3、用CONCAT(CONCAT(A_SN, '_'), LISTAGG(B_SN,'_') WITHIN GROUP (ORDER BY B_SN))代替了CONCAT(CAST(A_SN AS VARCHAR(1000)), '_', GROUP_CONCAT(CAST(B_SN AS VARCHAR(1000)),'_'))

WITH A1 AS(
	SELECT SN,
		OnOrbitRA,
		OnOrbitDec,
		InputMAGG,
		ACOS(-1)/180*OnOrbitRA RA,
		ACOS(-1)/180*OnOrbitDec aDEC,
		SIN(ACOS(-1)/180*OnOrbitDec) SIN_DEC,
		COS(ACOS(-1)/180*OnOrbitDec) COS_DEC
	FROM a
	),
B1 AS(
	SELECT SN,
		OnOrbitRA,
		OnOrbitDec,
		InputMAGG,
		ACOS(-1)/180*OnOrbitRA RA,
		ACOS(-1)/180*OnOrbitDec aDEC,
		SIN(ACOS(-1)/180*OnOrbitDec) SIN_DEC,
		COS(ACOS(-1)/180*OnOrbitDec) COS_DEC
	FROM b
	),
T0 AS (
	SELECT A1.SN A_SN,B1.SN B_SN,
		B1.OnOrbitRA B_OnOrbitRA,B1.OnOrbitDec B_OnOrbitDec,B1.InputMAGG B_InputMAGG,
		A1.OnOrbitRA A_OnOrbitRA,A1.OnOrbitDec A_OnOrbitDec,A1.InputMAGG A_InputMAGG
	FROM A1 JOIN B1  
		ON 	A1.OnOrbitDec>=B1.OnOrbitDec-0.5/3600 
			and A1.OnOrbitDec<=B1.OnOrbitDec+0.5/3600
			and A1.RA>=B1.RA-1.6548341646645552E-6 
			and A1.RA<=B1.RA+1.6548341646645552E-6
			and (SQRT(POWER(B1.COS_DEC*SIN(A1.RA-B1.RA),2)
				+POWER(A1.COS_DEC*B1.SIN_DEC-A1.SIN_DEC*B1.COS_DEC*COS(A1.RA-B1.RA),2))
				/(A1.SIN_DEC*B1.SIN_DEC+A1.COS_DEC*B1.COS_DEC*COS(A1.RA-B1.RA)))
				<=TAN((ACOS(-1)/180)*(0.3/3600))
	),
T1 AS (
	SELECT A_SN,B_SN,
		B_OnOrbitRA,B_OnOrbitDec,B_InputMAGG,
		A_OnOrbitRA,A_OnOrbitDec,A_InputMAGG,
		ROW_NUMBER() OVER ( PARTITION BY B_SN ORDER BY A_SN ) RN
	FROM T0
	), 
T2 AS (
	SELECT * FROM T1 WHERE RN=1
	),
T3 AS (
	SELECT A_SN SN, 1+COUNT(*) CNT, CONCAT(CONCAT(A_SN, '_'), LISTAGG(B_SN,'_') WITHIN GROUP(ORDER BY B_SN)) SN_COM,
		(A_OnOrbitRA+SUM(B_OnOrbitRA))/(COUNT(*)+1) OnOrbitRA, 
		(A_OnOrbitDec+SUM(B_OnOrbitDec))/(COUNT(*)+1) OnOrbitDec,
		(A_InputMAGG+SUM(B_InputMAGG))/(COUNT(*)+1) InputMAGG
	FROM T2 
	GROUP BY A_SN,A_OnOrbitRA,A_OnOrbitDec,A_InputMAGG
	)
SELECT * FROM T3
UNION ALL 
	SELECT SN, 1 CNT, NULL SN_COM, OnOrbitRA, OnOrbitDec, InputMAGG
	FROM A 
	WHERE NOT SN IN ( SELECT A_SN FROM T1 ) 
UNION ALL 
	SELECT SN, 1 CNT, NULL SN_COM, OnOrbitRA, OnOrbitDec, InputMAGG 
	FROM B 
	WHERE NOT SN IN ( SELECT B_SN FROM T1 );

六．SPL 测试

A

1

=now()

2

>radius=0.3/3600, delta_rad=0.5/3600, pi=pi()/180, std=tan(pi*radius)

3

=A=file("A.csv").import@tc(SN,InputMAGG,OnOrbitRA,OnOrbitDec).sort@m(OnOrbitDec) .derive@om(pi*OnOrbitRA:RA,pi*OnOrbitDec:DEC,sin(DEC):SIN_DEC, cos(DEC):COS_DEC,SN:AR)

4

=B=file("B.csv").import@tc(SN,InputMAGG,OnOrbitRA,OnOrbitDec).sort@m(OnOrbitDec) .derive@om(pi*OnOrbitRA:RA,pi*OnOrbitDec:DEC,sin(DEC):SIN_DEC, cos(DEC):COS_DEC)

5

=delta_ra=func(A11,B.max(abs(DEC)),std)

6

=B.derive@mo(OnOrbitDec-delta_rad:g, OnOrbitDec+delta_rad:h, RA-delta_ra:s,RA+delta_ra:e, A.select@b(between@b(OnOrbitDec,g:h)).select(RA>=s && RA<=e && (sqrt(power(COS_DEC*sin(B.RA-RA),2)+power(B.COS_DEC*SIN_DEC-B.SIN_DEC*COS_DEC*cos(B.RA-RA),2))/(B.SIN_DEC*SIN_DEC+B.COS_DEC*COS_DEC*cos(B.RA-RA)))<=std).min(SN):AR)

7

=(A|A6.select@m(AR)).groups@n(AR+1:SN; count(1):CNT, iterate(~~/"_"/SN,""):SN_COM, sum(OnOrbitRA):OnOrbitRA, sum(OnOrbitDec):OnOrbitDec, sum(InputMAGG):InputMAGG ).run@m(SN=SN-1, if(CNT==1,SN_COM=null,(SN_COM=mid(SN_COM,2),OnOrbitRA/=CNT,OnOrbitDec/=CNT,InputMAGG/=CNT)) )

8

=A7|A6.select@m(!AR).new(SN,1:CNT,null:SN_COM,OnOrbitRA,OnOrbitDec,InputMAGG)

9

=interval@s(A1,now())

A2 预算几个常数

A3-A4 读入 A、B 两张表，按 OnOrbitDec 排序，把 DEC 和 RA 转成弧度值，并提前算好 DEC 的 sin 和 cos 值

A5 算出 delta_ra

A6 用 B 找 A，找出 A 后选出 SN 最小的，因为要保持原序。由于 A 事先按 OnOrbitDec 排序了，所以对 OnOrbitDec 初筛时采用了二分法，可以极大地减少比较计算量

A7-A8 把匹配上的数据按要求的结果格式整理计算，同时把 A 和 B 中没有匹配上的记录也合并进去

A

B

C

11

func

12

=B11*B11+1

13

=a=-power(cos(A11),4)*B12

14

=b=-2*power(sin(A11),2)*power(cos(A11),2)*B12

15

=c=1-power(sin(A11),4)*B12

16

=sqrt(b*b-4*a*c)

17

=-(b-B16)/2/a

18

if abs(B17)<1

return acos(B17)

19

=-(b+B16)/2/a

20

if abs(B19)<1

return acos(B19)

21

return 0

A11 计算 delta_ra 的函数


七．测试结果

VM1（单位：秒）

数据规模

1万

10万

50万

Starrocks

5.87

211

执行一个小时后报错

Oracle

1.722

30

509

SPL

1.182

6.169

33.475

VM2（单位：秒）

数据规模

1万

10万

50万

Starrocks

8.15

423

未测试

Oracle

1.526

30

511

SPL

1.072

5.637

45.863

另外，在 VM1 上尝试了 SQL 无初筛的效果，Oracle 在 1 万行数据规模时 20 分钟内跑不出结果，而 Starrocks 在 1 万行时跑了 5.86 秒，和有初筛的结果差不多，在 10 万行时跑了 9 分 49 秒，比有初筛的慢了许多。总体看来 SQL 上增加初筛是有意义的。

八．结果点评

1、SPL 社区版的表现最好，远远超过 SQL 型数据库。

2、作为专业 OLAP 数据库的 Starrocks 在有初筛的情况下没有跑过 Oracle 是比较奇怪的现象，很可能是这里的非等值关联造成的，无法使用 HASH JOIN 算法时就只能硬计算了。看来对于复杂计算的优化，这些新兴数据库的能力还尚有不足。

3、SPL 优势的原因主要在于可以实现更优的算法，计算量会低很多。而 SQL 无法描述这种过程分步的运算，非等值关联无法优化，尽管初筛已经减少了很大一部分计算量，但剩余计算量仍然很大。

4、SPL 数据量比较小的时候，CPU 多看起来不起作用，原因可能是当数据量较小的时候，多个线程间匹配到的重复数据比较多，再多 CPU 的作用也就不大了。

5、测试结论

对于 SQL 无法自动优化的非常规计算任务，使用 SPL 能方便地写出适合算法的代码（事实上代码比 SQL 更短，开发也更简单），性能会比 SQL 大幅领先。


二分法(2) 集算器(484) SQL困难(18) 性能优化(158) 解决方案(56) 列式计算(1)