在建模数据中经常遇到这样一种变量，其本身是受因变量影响的（即它不但不是因变量的影响因素，反而因变量是它的影响因素），若该变量被作为自变量添加入模型，则会造成其他自变量不能进入模型。同时，由于这类变量是依附于因变量存在的，在实际预测应用时会得不到这些变量的数据，从而使得模型无法真正使用。对于这样的变量我们将其称为“伪自变量”。比如在贷款违约预测的变量中，同时含有用户是否违约和逾期天数两个变量，其中用户是否违约为预测目标即因变量，而逾期天数则就是受到因变量影响的，只有违约的客户逾期天数才会大于0，没有违约的客户逾期天数都为0，这样的变量就是伪自变量应该从建模数据中剔除。

例如在信用卡欺诈的数据中，构造一个伪自变量fraud_days，然后用易明建模外部库进行建模，通过观察模型指标AUC值和每个变量的重要度，识别出伪自变量。

A1 导入数据

A2 构造伪自变量fraud_days，当目标变量Class为0时，fraud_days=0，Class为1时，fraud_days为一个1到100的随机数

A3 初始化环境

A4 加载建模文件，生成md对象

A5 设置目标变量为Class

A6 执行自动建模

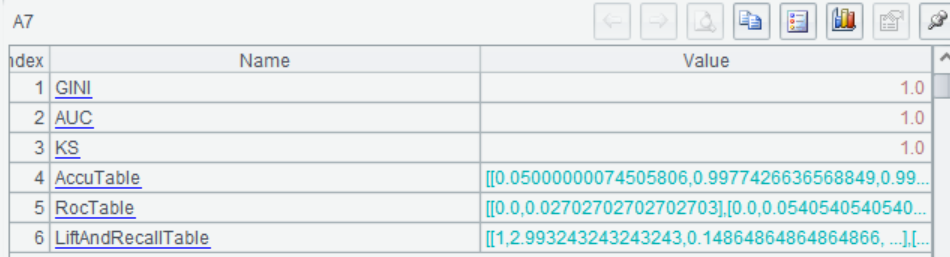
A7 读取模型表现指标，观察AUC值

A8 读取变量重要度，并降序排列

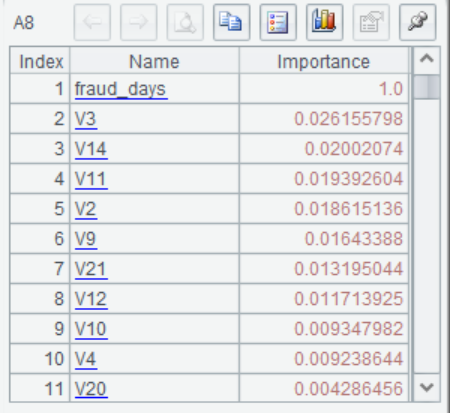
可以看到模型的AUC为1，实现了“完美预测”，但这种“完美”往往不是好现象，它意味着模型中出现了能够“完美解释”因变量的自变量，进一步观察各变量的重要度，发现我们构造出来的fraud_days重要度为1，其他变量为0或几乎为0，这说明在建立的模型中fraud_days在起作用，其他的变量都被排除在模型之外。这样的自变量即为伪自变量，建模时应当予以剔除。