对于时间序列来说，比较两个时间序列的相似性是一个很普遍的任务。通俗来说，两个时间序列的数据越接近，它们的图像“长得越像”，两个时间序列就越相似，而形容它们“长得像”的程度就是相似度，用sm表示。

假设用数学方法可以计算两个时间序列A、B的的相似度，用Sim(…)来表示这个方法，则：

sm=Sim(A,B)

理论上Sim(…)的函数形式有无穷多种，我们还是介绍一种简单有效的方法——动态时间规划（Dynamic Time Warping，简称DTW）。

如果两个时间序列是完全对齐（对应位置的点数值接近）的，只要计算两个时间序列数据对应位置的距离（如绝对差）之和即可，如下图中的两个时间序列：

图(a)(b)中的两个时间序列A、B完全对齐，两者非常相似，只要计算两者的距离之和即可，把它作为时间序列A、B的相似度sm。

sm=sum(|A_i-B_i|),i∈[1,n]

其中A_i是A的第i个元素，B_i是B的第i个元素，n是A、B的元素个数。

实际中的时间序列并不总是完全对齐的，但直观看上去两个时间序列还是“长的很像”，比如下图中的两个时间序列：

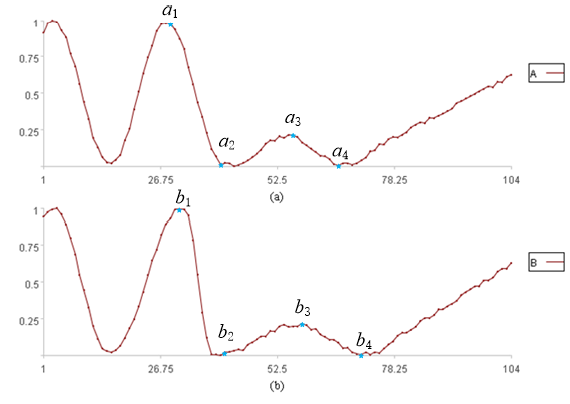
图(a)(b)中的两个时间序列整体上形状非常相似，但是它们在x轴上并不完全对齐，比如A上的a₁,a₂,a₃,a₄与B上的b₁,b₂,b₃,b₄应该一一对应，但是从图中很明显的看出，它们不能完全对齐。直接计算对应位置数据的距离之和不一定能得到两者相似的结果，遇到这种情况应该怎么做呢？

在比较两个时间序列的相似度之前，需要将其中一个（或者两个）时间序列在x轴上扭曲，以使两个时间序列对齐。

那如何才能使两个时间序列对齐呢？也就是说怎样扭曲才是正确的？直观上理解，当然是扭曲一个序列后可以与另一个序列重合，这时两个时间序列中所有对应点的距离之和是最小的。

假设我们有两个时间序列A和B，他们的长度是n：（DTW算法允许两个时间序列不等长，但无论是否等长，算法过程都是一样的，实际应用中等长的时间序列更常见，所以就以长度相等的时间序列来介绍了）

A= [a₁,a₂,…, a_n]

B= [b₁,b₂,…, b_n]

我们依然采用两个时间序列中对应点的距离来计算相似度，因为可以扭曲x轴，所以并不是在两个序列中依次取对应点来计算距离，而是每个点有可能对应另一个序列中的多个点，从下图中可以看到有这种情况发生：

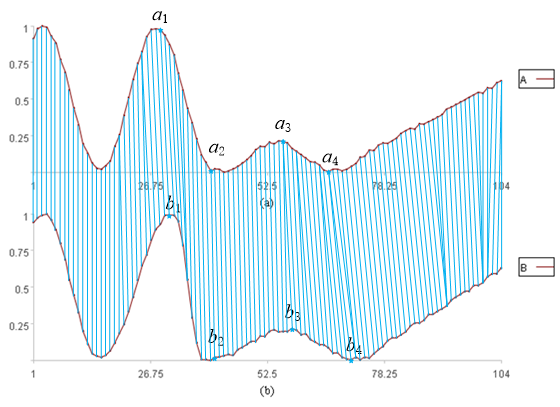
当然，扭曲x轴有一定要求：

1. 每个点都必须用到，不可跳过；

2. 时间序列中数据顺序不变；

3. 虽然可以“一对多”，但不可以交叉。

如果时间序列的长度是有限的，理论上扭曲x轴的方式就是有限的，只要穷举所有的扭曲方式，逐一计算扭曲后的两个时间序列的距离，距离最小时的扭曲方式就是我们需要的，但这样计算量太大，所以采用动态规划的方法来高效的完成计算。

为了对齐这两个序列，我们需要构造一个n*n的距离矩阵D，矩阵元素d_ij表示a_i和b_j两个点的距离（也就是时间序列A的每一个点和B的每一个点之间的距离，距离越小则相似度越高，这里先不考虑顺序），一般采用绝对差d_ij= |a_i-b_j|表示两点的距离。每一个矩阵元素表示点a_i和b_j对齐。DTW算法可以归结为寻找一条通过距离矩阵中若干个点的路径，路径通过的点即为两个序列进行计算的对齐的点，如下图：

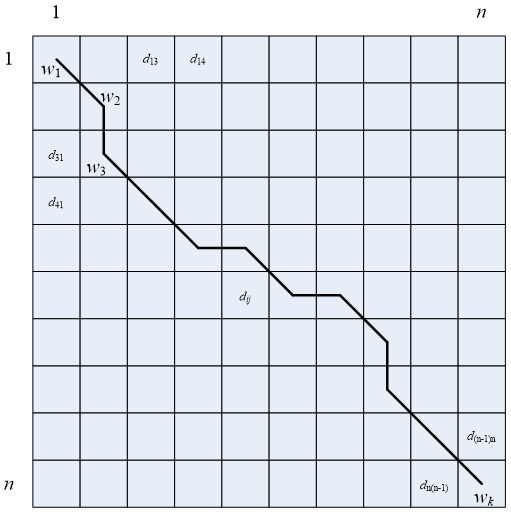
假设上图的网格就是距离矩阵D，每个格都是一个矩阵元素d_ij，图中的实线W是最短距离之和的路径，怎么才能找到这条W呢？

我们把这条路径定义为规整路径，用W来表示，W的第k个元素定义为w_k=(i,j)，定义了序列a_i和b_j的对应关系，即：

W=[w₁,w₂,…,w_k],k∈[n,2*n-1]

这条路径不是随意选择的，需要满足以下几个约束：

1. 边界条件

两个时间序列A、B的首尾位置必须对应，即a₁对应b₁，a_n对应b_n，因此所选的路径必定是从左上角出发，在右下角结束，即w₁=(1,1),w_n=(n,n)。

2. 连续性

如果w_m-1=(a’,b’)，那么对于路径的下一个点w_m=(a,b)需要满足 (a-a’)≤1和 (b-b’)≤1，也就是不可能跨过某个点去对齐，只能和自己相邻的点对齐。这样可以保证A和B中的每个坐标都在W中出现。

3. 单调性

如果w_m-1=(a’,b’)，那么对于路径的下一个点w_m=(a,b)需要满足(a-a’)≥0和(b-b’)≥0，这样就限制了W上面的点必须是随着时间单调进行的。

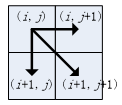
结合连续性和单调性约束，每一个格点的路径就只有三个方向了。比如路径已经通过了格点(i, j)，那么下一个通过的格点只可能是下列三种情况之一：(i+1, j)，(i, j+1)或者(i+1, j+1)，如下图：

满足上面这些约束条件的路径有近3ⁿ个，我们感兴趣的是使规整路径W经过的距离和最小，把它作为时间序列A、B的相似度sm：

sm=min(sum(D(w_i)))/n

其中D(w_i)是距离矩阵D按w_i的位置信息取距离，除以n是计算平均距离。

为了得到距离和最小的路径W，我们定义一个累加距离矩阵C，从(1, 1)点开始匹配两个时间序列A和B，每到一个点都累加之前所有点计算的距离，到达终点(n, n)后，这个累积距离就是我们上面说的总距离，也就是序列A和B的相似度sm。

累积距离c_ij可以按下面的方式表示，累积距离c_ij为当前距离d_ij(距离矩阵D第i行第j列的元素)与可以到达该点的最小的邻近元素的累积距离之和：

c_ij=α*d_ij+min(c_(i-1)(j-1),c_(i-1)j,c_i(j-1))

其中α是惩罚系数，用来对不同的路径进行惩罚，如不希望两个时间序列发生一对多时，可以使他们该路径的α大于1。

最佳路径W是使得延路径的积累距离达到最小值的这条路径，而最小值就是时间序列A、B的相似度。

sm=c_kk/n

SPL例程：

计算结果示例

距离矩阵D：

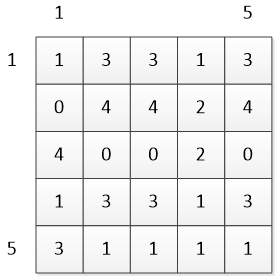
累计距离矩阵C：

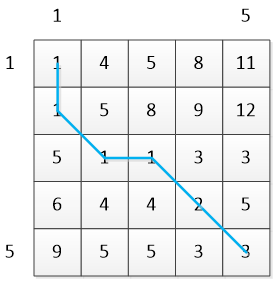
图中蓝色的线是最佳路径W

W=[(1,1),(2,1),(3,2),(3,3),(4,4),(5,5)]

最终的曲线相似度sm：

sm=3/5=0.6

两个时间序列的对应关系：

两个时间序列的对齐后的时间序列：

图(a)中是时间序列A、B，图(b)是它们对齐后的时间序列A2、B2，从图中可以明显看出对齐后，两个时间序列还是比较相似的。

例程中计算时间序列A、B相似度时用的是它们的原值，实际情况中两个时间序列的量纲可能不一致，所以可能需要对他们进行标准化（第4章的4.2节介绍过这些方法），而后才能用DTW计算它们的相似度。

DTW算法还支持多维空间的曲线计算相似度，只是距离要重新定义了（比如用欧式距离），其他计算过程是类似的。