时间序列中，如果某一时段内的数据变化不大，我们称之为稳定段；某一时段内数据快速上升或者下降，我们称之为不稳定段；不稳定段通常是前一段稳定段的结束，也是后一段稳定段的开始，发现不稳定段可以确定每一段稳定段的起止时间，这属于发现形状的问题，但相对较简单，只要找出区分平稳段和不平稳段的特征然后用异常发现的模型来做即可。

模型尝试

下图是两个稳定段多次切换的时间序列，其中红框时段是不稳定段：

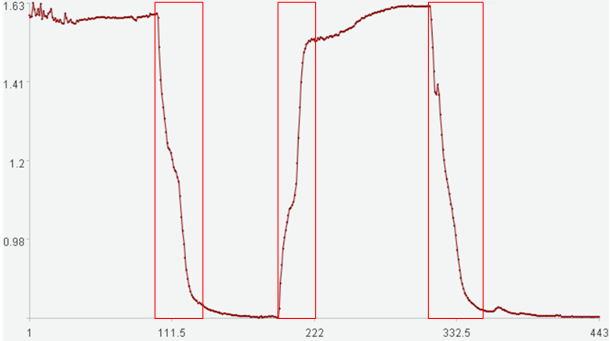
横轴是时间序列索引，纵轴是时间序列取值。

不稳定段处于两个稳定段之间，使用原值很难准确发现不稳定段的起止时间，考虑使用衍生时间序列来发现。稳定段的变化率小，不稳定段的变化率大，选择用变化率来完成此任务。

假设时间序列为X：

X= [x₁,x₂,…,x_n]

变化率C：

C=Fc(X)

Fc(…)是变化率函数。

异常度O：

O=E(C,arg₁,arg₂,…)

E(…)是异常发现函数，arg₁,arg₂,…是发现异常时需要的参数。

SPL例程

threshold(…)是阈值计算函数，这里选用距离法算阈值。

计算结果示例

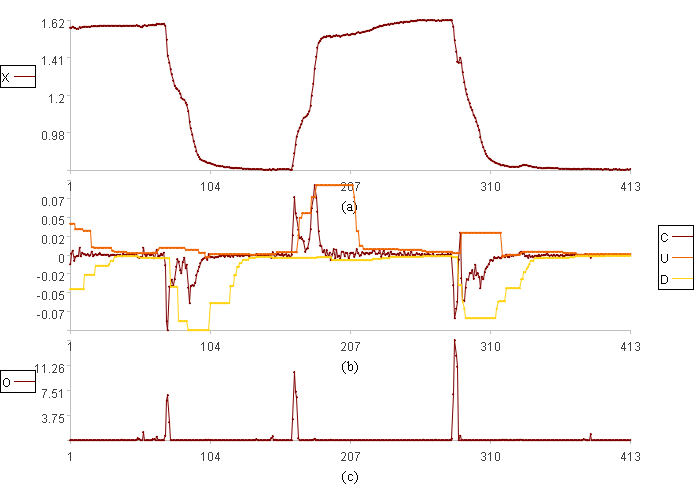
图(a)是时间序列X，图(b)是变化率C和它的上限U、下限D，图(c)是异常度O。因为学习长度是30，无法计算异常度，所以此图比原值图少30个数据。

模型优化

模型尝试并不算成功，只是发现了不稳定段的开始时间，异常并没有持续到不稳定段结束，但变化率这一衍生列是有效的，明显将稳定段和不稳定区分开了，只是计算过程中不稳定段的变化率陆续被用于计算阈值上下限了，导致上下限随之移动，影响了对后续变化率的判断。为了避免这种情况，可以考虑当变化率过大或过小时，不把当前时刻的变化率加入学习数据，这样阈值上下限就不会因变化率过大或过小而移动，从而准确发现不稳定段。另外学习数据应该包含当前时刻的变化率，这样可以使阈值上下限有机会取到当前时刻变化率，减少误判。

对模型做如下优化：

稳定段变化率很小，一般不会超过某个值，为平稳段变化率设置一个阈值（比如0.01），称为平稳阈值，记为c₀。

当变化率的绝对值大于等于平稳阈值时，不把该时刻的变化率加入到学习数据中，仍然延用之前的阈值上下限；当变化率绝对值小于平稳阈值时，正常更新学习数据，更新阈值上下限。

SPL例程

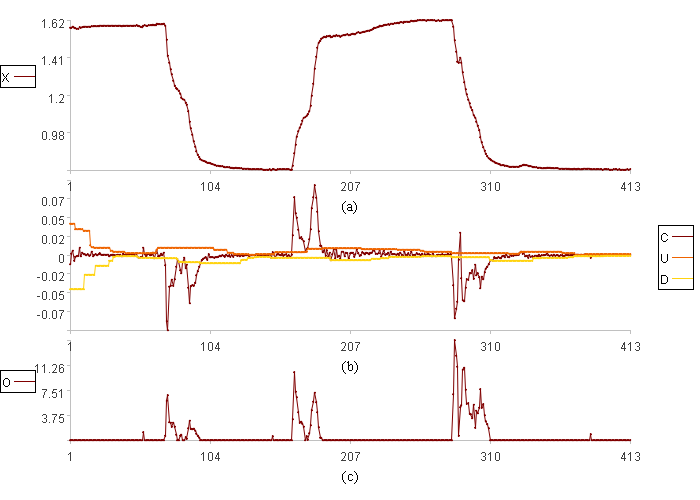
计算结果示例

模型精细化

模型优化后，异常度大于0时基本可以覆盖不稳定段，但平稳段还有一些小异常，不稳定段也有部分没有发现。这是因为平稳段有部分变化率较大，不平稳定段也有部分变化率较小，为了使结果更准确，可以将原值平滑化，即计算主线。主线的平稳段变化率更小，不平稳段的偶然变化也会被平滑掉，更容易准确发现不平稳段。

模型精细化内容：

计算主线M：

M=fit_main(X,k’)

其中fit_main(…)是最小二乘法拟合主线函数，k’是拟合时的平衡系数。

SPL例程

计算结果示例：

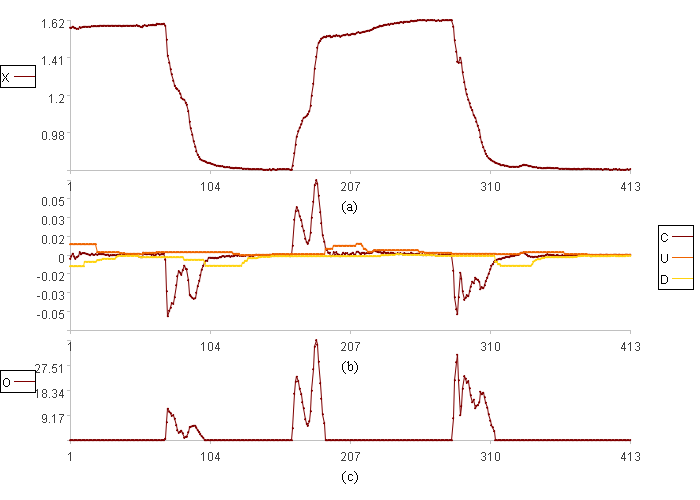
模型精细化后能准确发现不稳定段。

本例程只是一个案例，介绍了一种简单的发现形状案例，但是模型优化和精细化并非总是这么简单，这是一个复杂的过程，其实本例程还可以增加一些平稳段和不平稳段的衍生值（如波动频率，平稳段波动频率高，不平稳段波动频率低）作为辅助观察值来进一步优化模型，使不平稳段的发现更加准确。

根据工业环境和工艺知识不断优化模型是一项手艺活儿，只有锻造好自己的手艺才能真正提高工业生产效率和提升生产安全性。