2.5 波动幅度
波动幅度是描述原值波动大小的衍生序列。
通俗的讲,一段时间内最大值与最小值之差就可以作为波动幅度W。
wi=ma-mi
其中ma和mi是X[-l]i内的最大值和最小值。
但这么做会有隐患,当X中有特别大或特别小的值时,wi会持续一段时间(长度为l),受异常值影响很大。所以考虑将异常值去掉后,把正常数据的最大值、最小值以及当前值做差后的结果作为波动幅度W。
时间序列X的波动幅度序列W:
mu=max(Norm(X[-l]i))
md= min(Norm(X[-l]i))
其中mu、md分别是X[-l]i中正常数据的最大值和最小值,Norm(…)是之前介绍的异常发现方法(箱线图法、正态统计法、距离法),返回所有的正常数据。
SPL例程:
A |
B |
C |
|
1 |
=data=file(“1Ddata.csv”).import@tci().to(100) |
/时间序列X |
|
2 |
=l=5 |
/区间l |
|
3 |
=data.((if(#<=l,null,(xi=~,s=~[-l:-1],norm=func(A5,s,1.5), ma=max(norm),mi=min(norm),max(ma-xi,xi-mi,ma-mi))))) |
/波动幅度W,箱线图法中的四分位距倍数为1.5 |
|
4 |
/箱线图法,返回正常数据,参数:序列,四分位距倍数 |
||
5 |
func |
||
6 |
=A5.median(:4) |
||
7 |
=B6(1) |
/Q1 |
|
8 |
=B6(3) |
/Q3 |
|
9 |
=B8-B7 |
/IQR |
|
10 |
=B7-B9*B5 |
/td |
|
11 |
=B8+B9*B5 |
/tu |
|
12 |
=A5.select(~>=B10&&~<=B11) |
/正常值 |
|
A3格中计算波动幅度序列W;
A5代码块是箱线图发现异常法,返回所有正常数据,这里也可以换成其他的发现异常方法,比如正态统计法、距离法。
计算结果示例:
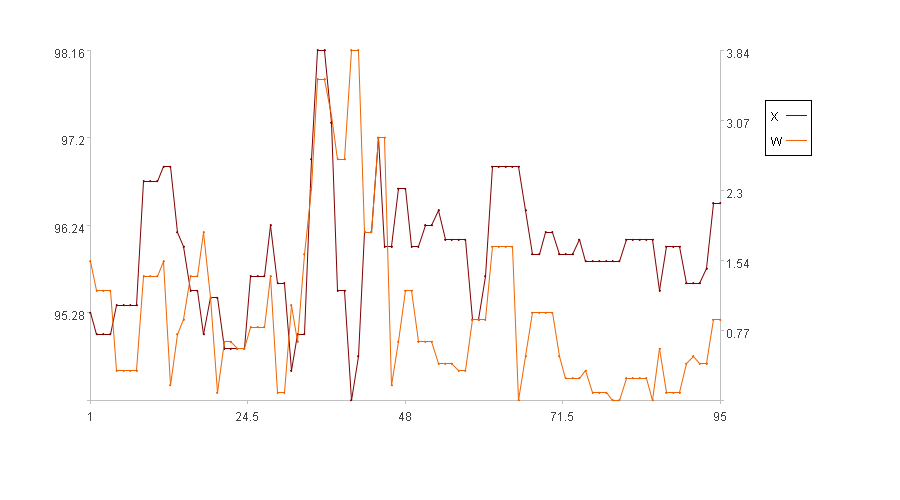
图中横轴是序列索引,左纵轴是原值X的取值,右纵轴是波动幅度W的取值。图例中X是原值,W是波动幅度。(前5个时刻没有波动幅度,图中只画了后95个时刻的波动幅度)
根据最大值和最小值算出的波动幅度只考虑原值本上的波动,没有考虑原值的趋势,比如当原值整体呈下降趋势时,波动的幅度会很大。所以波动幅度还可以考虑主线后再计算。
原值与主线对位相减后的序列称为波动序列,记为Wv,取Wv [-(l+1)]i+1内绝对值最大的前一半数的均值作为波动幅度wi。
时间序列X的波动幅度序列W:
Wv=X—M
tophi=top(-n\2,|Wv [-(l+1)]i+1|)
wi=avg(tophi)
其中|Wv [-(l+1)]i+1|是指Wv [-(l+1)]i+1的数都取绝对值,tophi是xi对应的|Wv [-(l+1)]i+1|中最大的前一半数。
SPL例程:
A |
B |
C |
|
1 |
=data=file(“1Ddata.csv”).import@tci().to(100) |
/时间序列X |
|
2 |
=l=5 |
/区间l |
|
3 |
=fit_main(A1,10) |
/主线M,k=10 |
|
4 |
=A1--A3 |
/波动序列Wv |
|
5 |
=A4.(if(#<=l,null,(s=~[-l:0],s.top(-(l+1)\2,abs(~)).avg()))) |
/波动幅度 |
|
A3格中是最小二乘法算出的主线(也可以用移动平均的方法算主线);
A5格中计算波动幅度序列W;
计算结果示例:
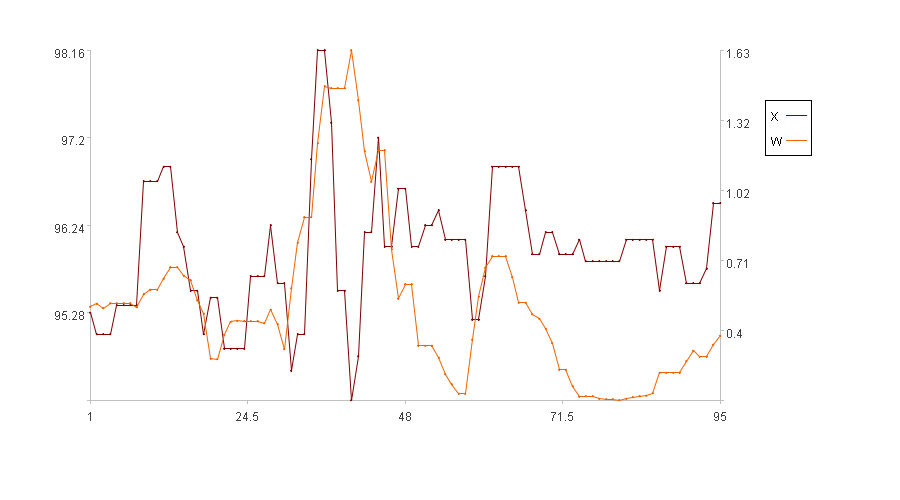
图中横轴是序列索引,左纵轴是原值X的取值,右纵轴是波动幅度W的取值。图例中X是原值,W是波动幅度。(前5个时刻没有波动幅度,图中只画了后95个时刻的波动幅度)



