原值的波动可能比较频繁，但整体上呈现某一种趋势，主线就是描述这种趋势的衍生序列。

通俗的讲，将原值平滑后就可以描述原值的趋势。平滑化最常见的手段的就是平均，具体到时间序列就是移动平均。

时间序列X的主线M：

m_i=avg(X[-(l+1)]_i+1)

SPL例程：

A3格中计算主线M；

思考：尝试用SPL实现线性加权移动平均和指数加权移动平均。

计算结果示例：

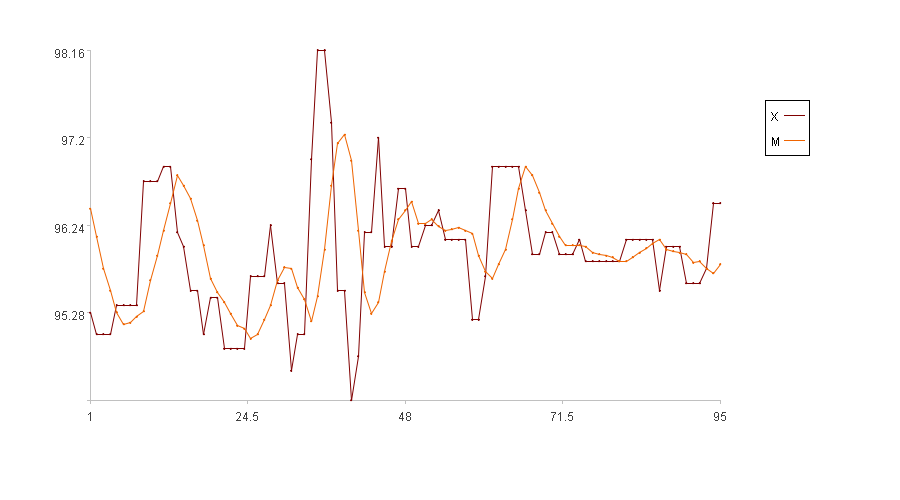
图中横轴是序列索引，纵轴是原值X的取值。图例中X是原值，M是主线。（前5个时刻没有主线，图中只画了后95个时刻的主线）

移动平均方便计算，平滑效果也不错，但缺点也很明显，比如主线上的每个点都是之前某个区间所有值的平均，这就必然导致主线整体延迟于原值，即原值开始下降时，主线可能还保持原来的状态，延迟一段时间后主线才会下降。这会导致异常发现不够及时，对即时性要求高的场景不太适合选用此方法。

我们再换一种方法计算主线。

主线要表征原值的信息，所以原则上要与原值接近；主线还要平滑，所以相邻点也要接近。假设已经计算出主线，我们把主线与原值的绝对差之和称为原值距离，主线上相邻点的绝对差之和称为主线距离。合适的主线应该使这两种距离都尽量小，那么对这两类距离加权合计后求其最小值即可得到合适的主线M。

这种方法计算的主线将权衡两类距离，延迟效应不明显，及时性很好，适合对即时性要求高的场景。但它也有自己的缺点，计算复杂度相较于移动平均高不少，对计算效率要求高的场景要慎用。

1. 计算距离

主线距离是主线上相邻两点的距离(差的平方和)的总和，记为MD。

MD=sum(m_i-m_i-1)²

原值距离是主线与原值的距离(差的平方和)的总和，记为VD。

VD=sum(m_i-x_i)²

2. 两类距离加权后的最小值

设置平衡系数k来平衡两类距离的权重，则总距离D

D=VD+k*MD

3. 优化m_i使总距离D最短

对每个m_i求偏导：

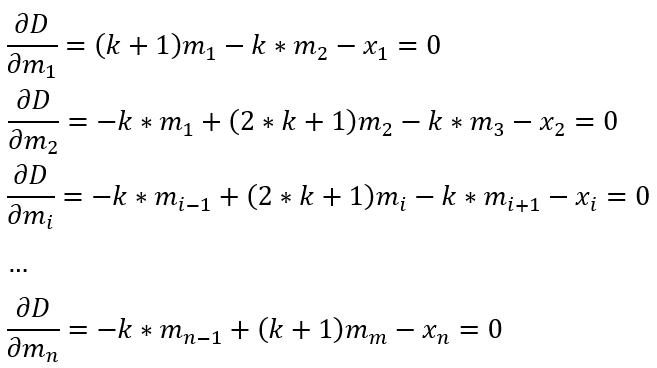
转换后的问题变为解多元线性方程问题。

系数矩阵用Cm表示

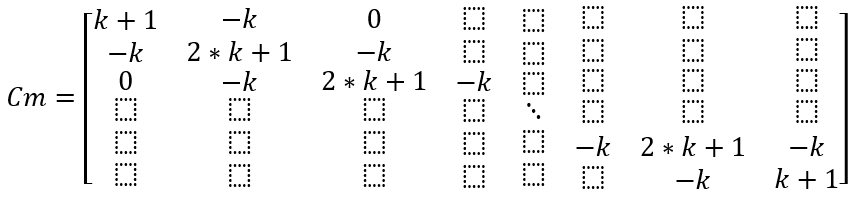
矩阵中未填写数值处都是0。

Cm*M=X

解上述方程就得到了主线M。

M=linefit(Cm,X)

其中linefit()是解线性方程的函数。

平衡系数k调节两类距离的权重，k越大，主线距离MD占比越大，主线越平滑，k越小，原值距离VD占比越大，主线越接近原值。当k=0时，主线就是原值。当k=∞时，主线是一个常数，常数值等于原值的平均值。

SPL例程：

A4格构造系数矩阵Cm；

A5格计算主线序列M。

计算结果示例：

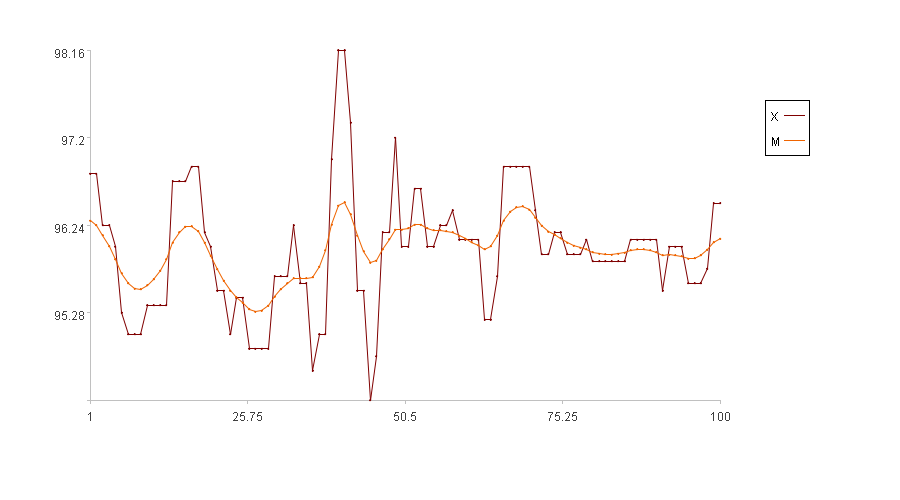
图中横轴是序列索引，纵轴是原值X的取值。图例中X是原值，M是主线。