2.3 离散度
离散度是描述原值分布情况的衍生序列。
在统计学上经常使用方差来衡量一组数的离散程度,我们也可以延用方差来计算离散度,称为方差方法。
时间序列X的离散度序列S:
si=sum((xj-a)2)/(n-1),j∈[1,n]
其中n是X[-(l+1)]i+1的长度n=l+1,xj是X[-(l+1)]i+1中的第j个元素,a是X[-(l+1)]i+1的平均数。
SPL例程:
A |
B |
C |
|
1 |
=data=file(“1Ddata.csv”).import@tci().to(100) |
/时间序列X |
|
2 |
=l=5 |
/区间l |
|
3 |
=data.((if(#<=l,null,(s=~[-l:0],var@s(s))))) |
/离散程度S |
|
A3格中计算离散度序列S,var@s(...)是计算方差的函数。
计算结果示例:
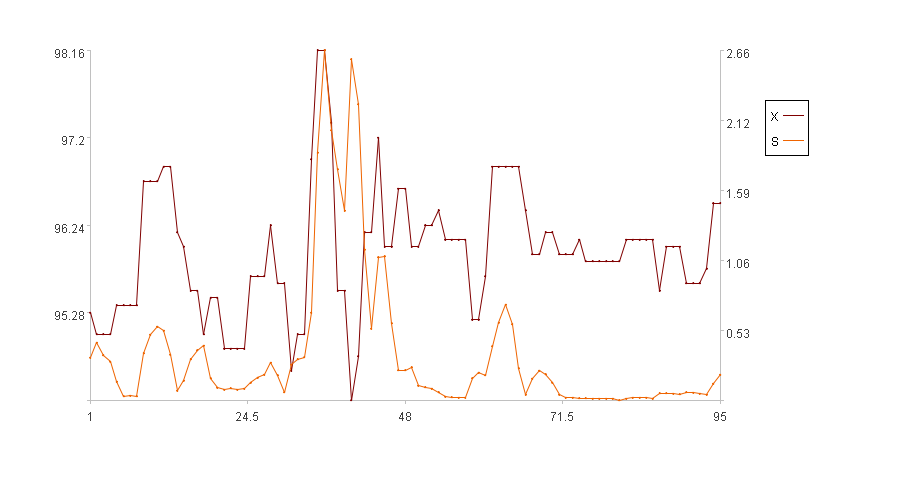
图中横轴是序列索引,左纵轴是原值X的取值,右纵轴是离散度S的取值。图例中X是原值,S是离散度。(前5个时刻没有离散程度,图中只画了后95个时刻的离散程度)



