1.7 通道阈值调整
对于大多数数据来说,百分比阈值调整法都可以满足需求,但有一些特殊数据是它无能为力的,如下图这个时间序列:
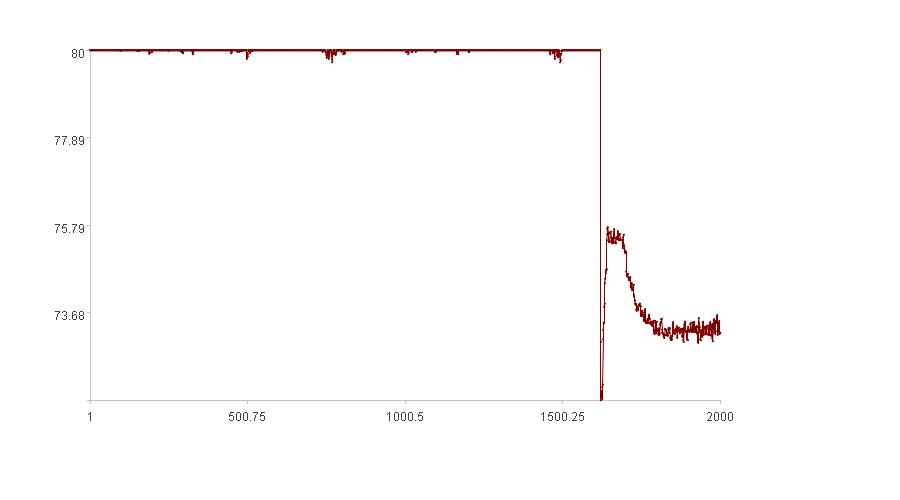
图中时间序列前半段数据都在80附近,后半段突然下降,调整后稳定在73附近,直觉上调整的过程是异常时段,其他时段都可以认为是正常。
先按原来的参数发现异常:
学习区间k=100;
距离法半径倍数n=2;
阈值差百分比dst=0。
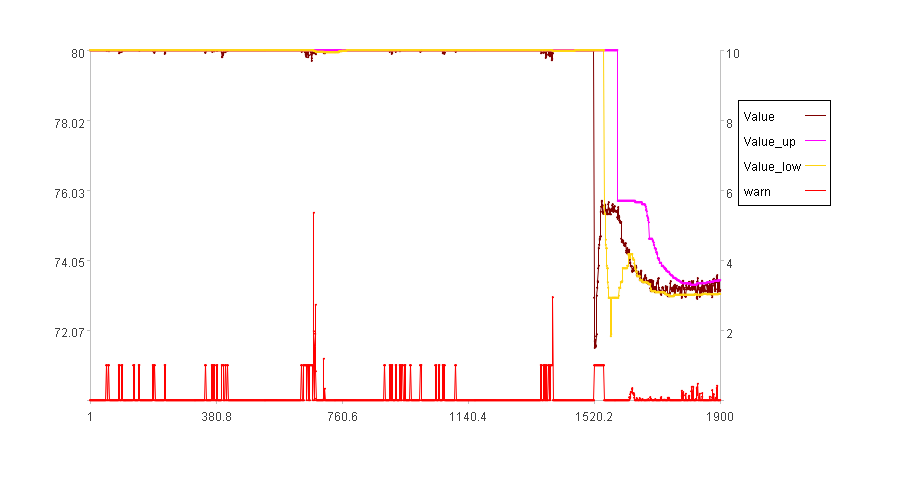
发现的异常符合算法的逻辑,80附近的突变点的确属于少数,可以认为是异常,但相较于调整时段的变化幅度,这样的变化根本不算什么,可以认为是正常的。
观察tu和td,两者在前半段相差很小,甚至相等,此时用百分比阈值调整法是无法调整异常度的。
下图是dst=0.3的异常发现结果:
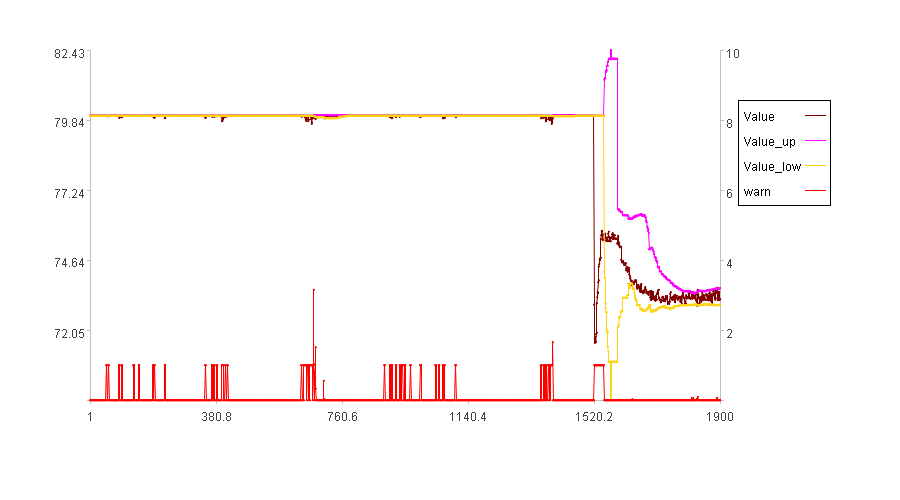
可以发现dst几乎没有作用,面对这类数据应该怎么做呢?
对于这类数据,我们允许时间序列X中的值在某个范围内变化,无论其在该范围内怎么变化,都认为是正常的。如上图的数据,允许数据的变化范围不超过0.5,就像一个“管道”似的,只要数据在这个宽度的“管道”内,都可以认为是正常的,将这个管道称为通道,用ch表示。利用通道调整阈值的方法称为通道阈值调整法。
通道阈值调整法也很简单:当xi大于tu时且td+ch也大于tu时,将tu调整为tu’=td+ch;当xi小于td时且tu-ch也小于td时,将td调整为td’=tu-ch。
tu’=if(xi>tu&&td+ch>tu, td+ch,tu)
td’=if(xi<td&&tu-ch<td, tu-ch,td)
这样就可以保证在通道ch内,xi都是正常的。
SPL
A |
B |
|
1 |
=file(C1).import@tci() |
/时间序列X |
2 |
100 |
/学习区间k |
3 |
2 |
/半径倍数 |
4 |
0.5 |
/ch |
5 |
=A1.(if(#<=A2,,Threshold(~[-A2:-1],"up",A3))) |
/阈值上限 |
6 |
=A1.(if(#<=A2,,Threshold(~[-A2:-1],"down",A3))) |
/阈值下限 |
7 |
=to(A2+1,A1.len()) |
/有效X索引 |
8 |
=A1(A7) |
/有效X |
9 |
=A5(A7) |
/tu |
10 |
=A6(A7) |
/td |
11 |
=A9.(if(A8(#)>~&&A10(#)+A4>~,A10(#)+A4,~)) |
/tu' |
12 |
=A10.(if(A8(#)<~&&A9(#)-A4<~,A9(#)-A4,~)) |
/td' |
13 |
=A8.((a=max(~-A11(#),A12(#)-~,0),b=(A11(#)-A12(#)),if(a==0,0,if(b==0,1,a/b)))) |
/异常度Od |
计算结果示例:
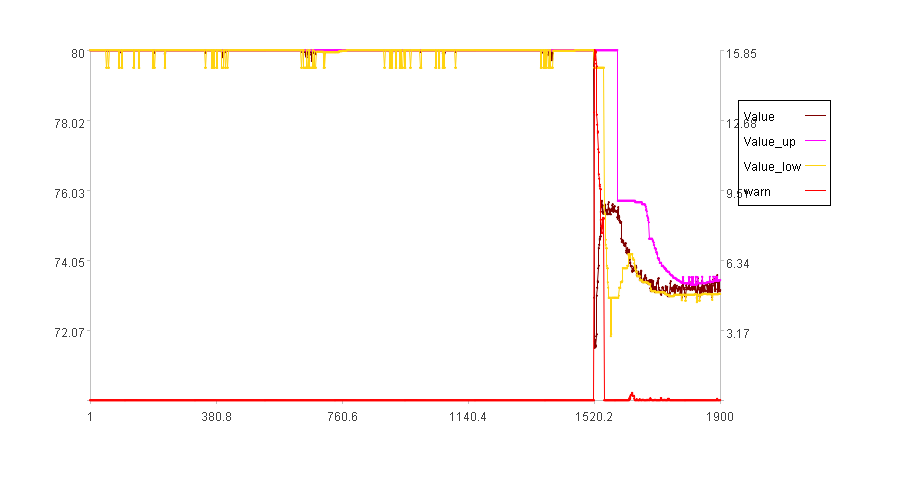
从图中可以看到,在通道内的数据都是正常了,也符合我们的直观判断。



