1.5 极值
箱线图法、正态统计法、距离法都是用X[-k]i的全部数据学习tu、td,计算复杂多相对高,尤其是距离法,计算复杂度是O(n2)。tu、td是数据中除异常点外的最大和最小值,我们可以用较大的一部分数据计算tu,较小的一部分数据计算td,这样就可以大大降低计算复杂度。
数学上极值这样定义:若函数f(x)在x0的一个邻域D有定义,且对D的所有点,都有f(x)<f(x0),则称f(x0)是函数f(x0)的一个极大值。同理,若对D的所有点,都有f(x)>f(x0),则称f(x0)是函数f(x)的一个极小值。
时间序列的极值可以类似描述,时间序列X中,若xi大于它之前1个区间的所有值且不小于之后1个区间的所有值,就称xi是极大值。同理,如果xi小于它之前1个区间的所有值且不大于之后1个区间的所有值,就称xi是极小值
极大值刚好是数据中较大的一部分,可以用来算tu,极小值是较小的一部分,可以用来算td。计算的方法是一样的,区别是原来用X[-k]i算tu、td。现在用X[-k]i中的极大值算tu,X[-k]i中的极小值算td。
极值的计算很简单:
令
Z=X[-k]i
极大值序列Mav
Mav=[zj, zj>max(Z[-l]j)&&zj≥max(Z[-l]j)]
极小值序列Miv
Miv=[zj, zj<min(Z[-l]j)&&zj≤=min(Z[-l]j)]
其中l是计算极值的区间长度。
还有一点需要注意,当Z是单调增、单调减或者常数的曲线时,极大值和极小值可能不存在或数量很少,无法描述整体数据的情况,此时不适合用极值来计算tu、td。
SPL例程
A |
B |
|
1 |
=data=file(B1).import@tci().to(100) |
|
2 |
1 |
/l |
3 |
=A1.len() |
|
4 |
=A1.select(#>A2&&#<=A3-A2&&~>~[-A2,-1].max()&&~>=~[1,A2].max()) |
/极大值序列Mav |
5 |
=A1.select(#>A2&&#<=A3-A2&&~<~[-A2,-1].min()&&~<=~[1,A2].min()) |
/极小值序列Miv |
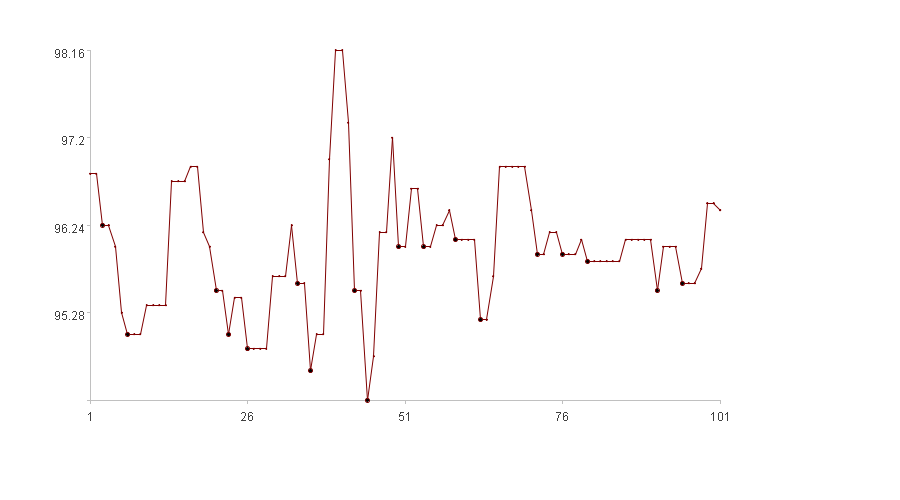
计算结果示例:
极大值(图中的加粗点)
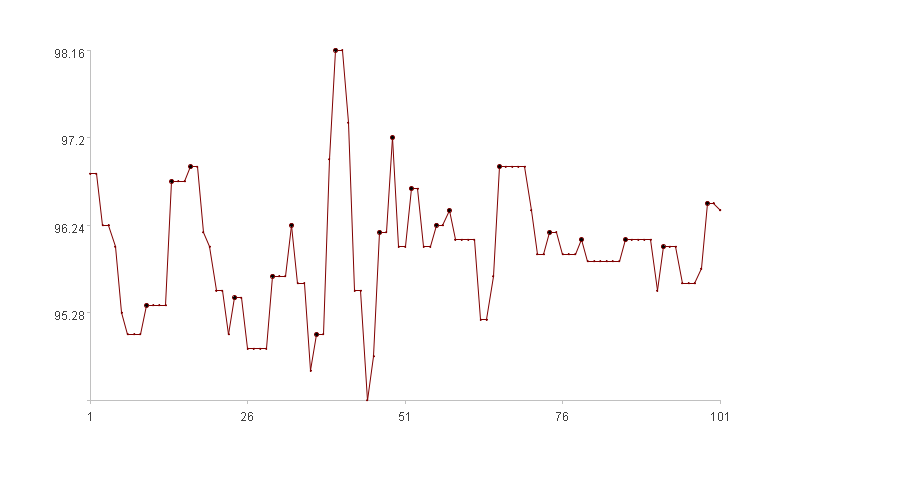
极小值(图中的加粗点)