数据中远离其他点的数据是不常见数据，比较数据中的每个点与其他所有点的距离（绝对差）之和，以最小距离和作为基准，超过该基准一定倍数的点就是异常值。

找出距离其他点都“不远”的数据，可以认为这些是正常数据，正常数据的最大值与最小值之外的数据可以认为是异常数据。

选定阈值型异常度函数：

TA[tu,td](x)=max(x-tu, td-x,0)/(tu-td)

其中tu、td是通过X[-k]_i学习得到的上下限。

用X[-k]_i计算tu、td的方法如下：

1.计算X[-k]_i中每个点到其他所有点的距离和

第p个点x_p的距离和记为d_p

d_p=sum(|x_p-x_q|),x_q∈X[-k]_i

其中x_p是X[-k]_i中的第p个点，x_q是X[-k]_i中的第q个点。距离和形成的序列用D表示。

2.最小距离和记为dmi

dmi=min(D)

3.将不大于n倍最小距离和（n*dmi）的x_p序列看作距离其他点“不远”的数据，记为SX，把它的最小值作为下限值td，最大值最为上限值tu。

SX=[x_p,d_p≤n*dmi]

td=min(SX)

u= max(SX)

异常度od这样计算：

od=max(x_i-tu, td-x_i,0)/(tu-td)

SPL例程：

调整n的大小可以调整上下限， n的默认值可以设置为2。

计算结果示例：

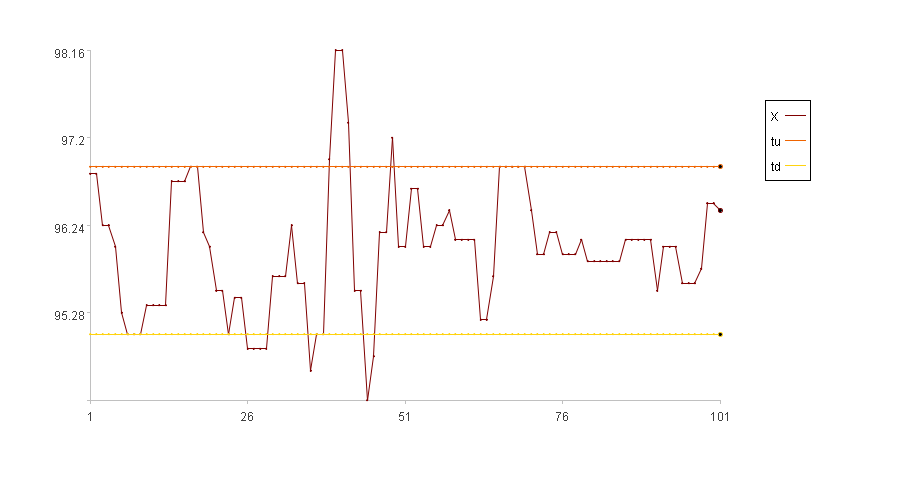
x_i在tu和td之间，所以异常度是0。