1.3 正态统计法
标准的正态分布,三个标准差(σ)覆盖的范围内,可以覆盖99.7%的数据,那么在 3σ 以外的数据就可以认定为异常点。
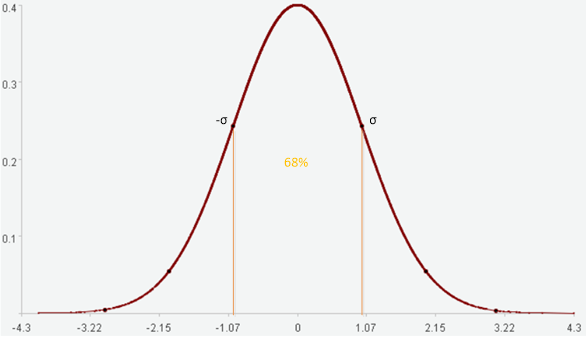
1个标准差内可以覆盖68%的数据。
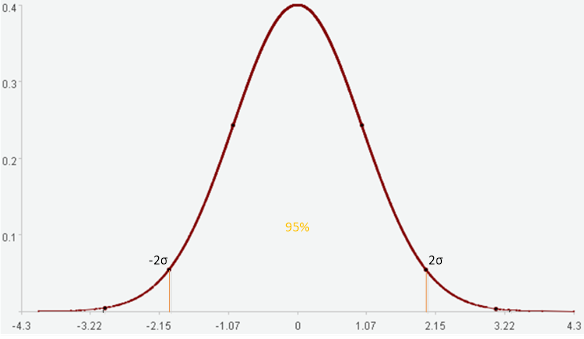
2个标准差内可以覆盖95%的数据。
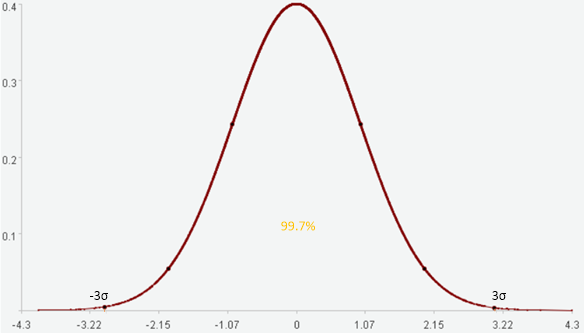
3个标准差内可以覆盖99.7%的数据。
正态分布的特点决定了n倍标准差范围外的数据是不常见数据,可以认为是异常。
选定阈值型异常度函数:
TA[tu,td](x)=max(x-tu, td-x,0)/(tu-td)
用X[-k]i计算tu、td的方法如下:
a=avg(X[-k]i)
σ=std(X[-k]i)
tu=a+n*σ
td=a-n*σ
其中a是X[-k]i的平均数,σ是X[-k]i的标准差,n是标准差倍数,调节它可以调节tu、td的大小。
异常度od这样计算:
od=max(xi-tu, td-xi,0)/(tu-td)
SPL例程:
A |
B |
|
1 |
=data=file(“1Ddata.csv”).import@tci().to(100) |
|
2 |
=n=3 |
/标准差倍数 |
3 |
=ldata=data.m(:100) |
/区间是100的学习数据x[-k]i |
4 |
=xi=data(101) |
/xi |
5 |
=a=A3.avg() |
/平均数a |
6 |
=sigma=sqrt(var@s(A3)) |
/标准差σ |
7 |
=td=a-n*sigma |
/下限td |
8 |
=tu=a+n*sigma |
/上限tu |
9 |
=od=max(xi-tu,td-xi,0)/(tu-td) |
/异常度od |
调整n的大小可以调整上下限, n的默认值可以设置为3。
计算结果示例:
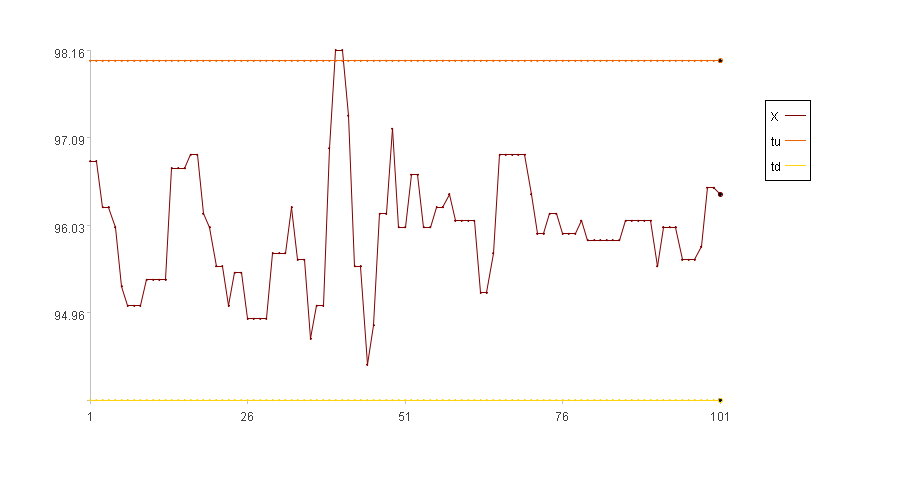
xi在tu和td之间,所以异常度是0。



