1.2 箱线图法
箱线图(Box Plot)是由一组或多组连续型定量数据的「最小观测值」、第一四分位数、中位数、第三分位数和「最大观测值」来反映数据的分布情况的统计图,因外形似箱子而得名。
箱线图的外形组成:
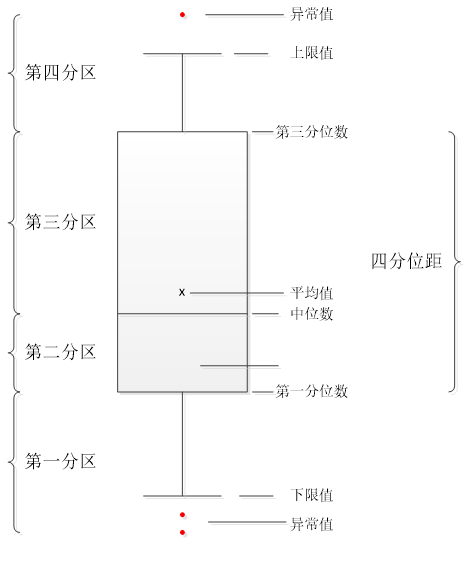
从箱线图的外形组成图中可以看出,上下限之间包含了大部分数据,少数数据被排除在上下限之外,这些数据不常见,可以认为是异常值。
选定阈值型异常度函数:
TA[tu,td](x)=max(x-tu, td-x,0)/(tu-td)
用X[-k]i计算tu、td的方法如下:
tu=Q3+n*IQR
td=Q1-n*IQR
其中Q1是第1四分位数,Q3是第3四分位数,n是四分位距的倍数,调节它可以调节tu、td的大小。
异常度用od表示,可以这样计算:
od=max(xi-tu, td-xi,0)/( tu-td)
SPL例程:
A |
B |
|
1 |
=data=file(“1Ddata.csv”).import@tci().to(100) |
/数据 |
2 |
=n=1.5 |
/分位距倍数 |
3 |
=ldata=data.m(:100) |
/区间是100的学习数据x[-k]i |
4 |
=xi=data(101) |
/xi,需要判断是否异常的数据 |
5 |
=ldata.median(:4) |
/3个四分位数 |
6 |
=Q1=A5(1) |
/第1四分位数Q1 |
7 |
=Q3=A5(3) |
/第3四分位数Q3 |
8 |
=IQR=Q3-Q1 |
/四分位距IQR |
9 |
=td=Q1-n*IQR |
/下限td |
10 |
=tu=Q3+n*IQR |
/上限tu |
11 |
=rg=max(xi-tu,td-xi,0)/(tu-td) |
/异常度od |
import@i()当数据只有1列时,返回序列。
A.median(:k)将数据k等分,返回k-1个分段值。调节n的大小可以调节tu、td的值,n的取值通常在[1.5,3]之间。
计算结果示例:
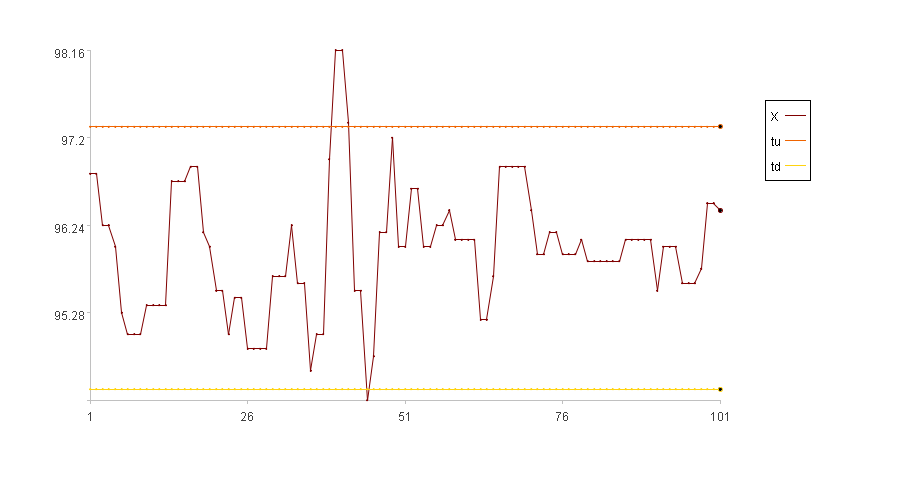
图中横轴是序列索引,纵轴是序列值。图例中X是数据值,tu是阈值上限,td是阈值下限(说明:tu和td都是数值,为了展示清晰画成线),最后一个加粗的点是xi,它在tu和td之间,所以异常度是0。



