11.13 函数递归:海盗分金问题
递归调用函数解决海盗分金问题。
海盗分金问题:
5 个海盗抢得 100 枚金币,他们按抽签的顺序依次提方案:首先由 1 号提出分配方案,然后 5 人表决,投票要超过半数同意方案才被通过,否则他将被扔入大海喂鲨鱼,依此类推。
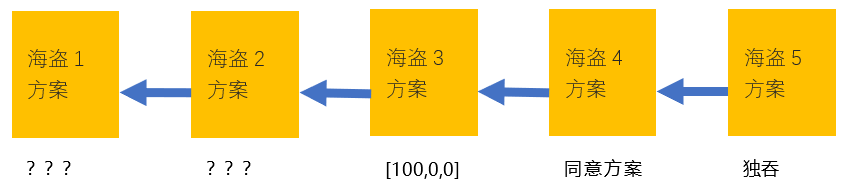
当只有两个海盗时,海盗 5 会否决海盗 4 的任何方案,独吞 100 金币。所以海盗 4 为了保命,会无条件同意海盗 3 方案。知道了海盗 4 的想法,贪婪的海盗 3 一定会给出 [100,0,0] 的分配方案。依此类推。
使用 func(c,…) 函数进行递归运算。
脚本:
| A | B | C | D | |
|---|---|---|---|---|
| 1 | func | |||
| 2 | if(A1==2) | return [-1,B1] | ||
| 3 | =func(A1,A1-1,B1) | |||
| 4 | =B3.psort() | =A1/2 | ||
| 5 | for B4.len() | if (B5<=C4) | =B3(B4(B5))+=1 | |
| 6 | >B1-=D5 | |||
| 7 | else | >B3(B4(B5))=0 | ||
| 8 | return B1 | B3 | |||
| 9 | =func(A1,5,100) | |||
B2-C2 只有 2 个海盗时, 最后一个海盗全拿
B3 使用 func() 函数,递归计算自己被否决后,剩下海盗会采用的方案
B4-C4 对该方案排序, 计算除了自己还需要几个海盗支持
B5-C5 争取分配最少的海盗们支持,多给 1 金币
C6 总金币里扣除分配的金币,剩下是自己的
C7 剩下的海盗分配 0 金币
B8 返回自己剩下的金币和修改后的方案,就是自己的分配方案。
A9 执行 func() 函数,参数是 5 个海盗,100 个金币
运行结果:
| Member |
|---|
| 97 |
| 0 |
| 1 |
| 2 |
| 0 |




代码中的 C2 格,两个海盗的时候,是不是要返回 [0,100]?
1、当只有海盗 5 的时候,独得金币 100,此时返回 [海盗 5]=>[100];
2、当海盗 4 加入分配时,根据自身利益最大化原则,海盗 5 无论如何都想独吞,而海盗 4 为了保命只好同意海盗 5 的方案,此时返回 [海盗 4, 海盗 5]=>[0,100];
3、当海盗 3 加入分配时,为了获取半数以上的支持,得拉拢原先获利最少的那几个海盗,所以海盗 3 会分一个金币给海盗 4,得到两个支持者 (自己肯定支持自己),此时就不用管海盗 5 了,分配方案为 [海盗 3, 海盗 4, 海盗 5]=>[99,1,0];
4、当海盗 2 加入分配,小心思也是一样的,尽量拉拢获利最少的那些海盗,所以为了自身获利最大,海盗 2 会用 2 个金币得到海盗 4 和海盗 5 的支持,各分配 1 个。此时得到的方案是 [海盗 2, 海盗 3, 海盗 4, 海盗 5]=>[97,0,2,1]
5、海盗 1 加入分配时,同样的手法,为了得到获利最少者的支持,会给海盗 3 和海盗 5 各一个金币,此时返回 [97,0,1,0,2]