11.12 函数递归:汉诺塔问题
递归调用函数解决汉诺塔问题。
汉诺塔问题是递归的经典问题。把 A 杆上的圆盘全部移到 C 杆上,并仍保持原有顺序叠好。每次移动一个圆盘,移动时要始终保持大盘在下,小盘在上。
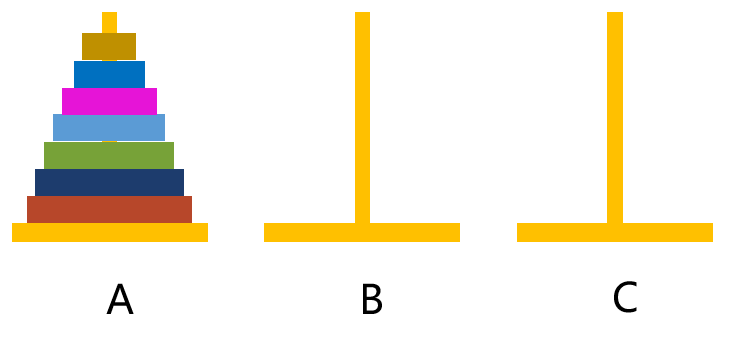
盘子从小到大依次命名为 1 到 n。我们总是把 n 个盘子看成第 n 个盘子和 n-1 个盘子两组。把 n-1 个盘子移动到 B,把第 n 个盘子移动到 C,再把 n-1 个盘子移动到 C 即可。
使用 func(c,…) 函数进行递归运算。
脚本:
| A | B | C | |
|---|---|---|---|
| 1 | func | ||
| 2 | if(A1==1) | >output("move disk" + string(A1) + "from" + B1 + "to" + D1) | |
| 3 | else | >func(A1,A1-1,B1,D1,C1) | |
| 4 | >output("move disk" + string(A1) + "from" + B1 + "to" + D1) | ||
| 5 | >func(A1,A1-1,C1,B1,D1) | ||
| 6 | >func(A1,5,“A”,“B”,“C”) | ||
A1 定义函数
B2-C2 圆盘只有一个时移动到 C
C3 将 A 上的 n-1 个盘子移动到 B
C4 将 A 最下面的盘子移动到 C
C5 将 B 上的 n-1 个盘子移动到 A
A6 函数有 4 个参数,分别是盘子个数(也是名称)、初始塔、中介塔和目标塔。
当 A 上有 5 个盘子时,输出结果如下图:




