最小二乘法线性拟合
最小二乘数据拟合的步骤为：
给定一组数据点(x1,y1)，(x2,y2)……(xm,ym)
（1）确定用于拟合数据的曲线类型，例如，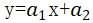
（2）将数据点代入曲线，得到系统AX=Y
（3）使用linefit()线性最小二乘法求解AX=Y
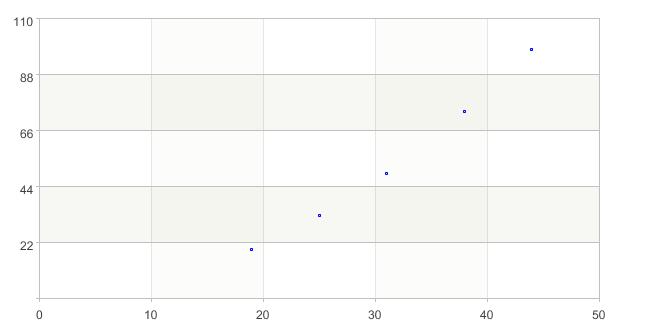
例如，用最小二乘法拟合下表中的数据
x |
19 |
25 |
31 |
38 |
44 |
y |
19 |
32.3 |
49 |
73.3 |
97.8 |
SPL代码如下：
A |
|
1 |
[19,25,31,38,44] |
2 |
[19,32.3,49,73.3,97.8] |
3 |
=canvas() |
=A3.plot("NumericAxis","name":"x") |
|
5 |
=A3.plot("NumericAxis","name":"y","location":2) |
6 |
=A3.plot("Dot","lineWeight":0,"lineColor":-16776961,"markerWeight":1,"axis1":"x","data1":A1,"axis2":"y","data2": A2) |
7 |
=A3.draw(800,400) |
8 |
[[19,1],[25,1],[31,1],[38,1],[44,1]] |
9 |
=linefit(A8,A2).conj() |
10 |
=to(10,50) |
11 |
=A10.([~,A9(1)*~+A9(2)]) |
12 |
=A3.plot("Line","markerStyle":0,"axis1":"x","data1":A11.(~(1)),"axis2":"y", "data2":A11.(~(2))) |
13 |
=A3.draw(800,400) |
A1-A7导入数据，画出散点图，确定曲线类型
A3 生成画布
A4 绘制横轴”x”
A5 绘制纵轴”y”
A6 绘制点图元，x 轴数据取 A1，y 轴数据取 A2
A7 画图，观察点的分布呈直线型，选取拟合曲线类型为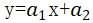
A8-A9 得到系统AX=Y，并求解拟合曲线
将数据点带入曲线并写成矩阵形式，得到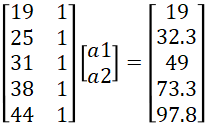
，即AX=Y形式。
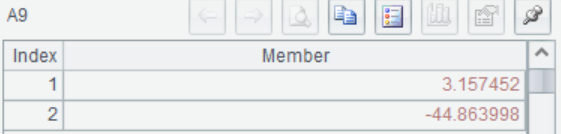
将矩阵参数传入linefit(A,Y)，求解出a1，a2的值，a1=3.157452，a2=-44.8639981
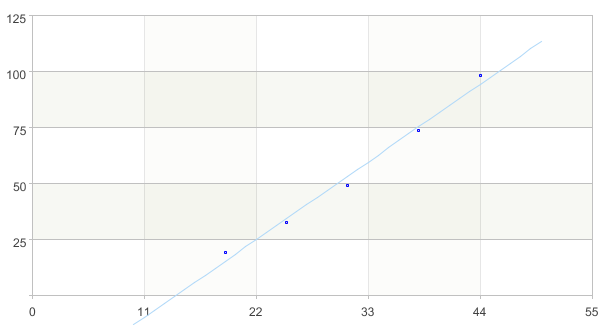
A10-A13将拟合曲线画到散点图上，直观对比
A10根据点的分布，选取10-50 的区间作图
A11区间内循环取数，生成x 轴和 y 轴数据
A12绘制线图元
A13 画图
可以用线性最小二乘法linefit() 拟合的曲线类型有多种，常用的曲线有：
（1）直线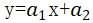
（2）多项式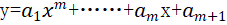
（3）双曲线（一支）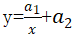
（4）指数曲线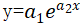
对于双曲线和指数曲线，需做变量代换，转化为对a1，a2的线性函数
