pca 降维
主成分分析是一种常用的降维方法,能将许多相关性很高的变量转化成少数几个彼此相互独立或不相关的变量。例如,有一份6 个样本,4 个变量的数据
x1 |
x2 |
x3 |
x4 |
|
1 |
7 |
26 |
6 |
60 |
2 |
1 |
29 |
15 |
52 |
3 |
11 |
56 |
8 |
20 |
4 |
11 |
31 |
8 |
47 |
5 |
7 |
52 |
6 |
33 |
6 |
11 |
55 |
9 |
22 |
对x1,x2,x3,x4 降维,代码如下:
A |
|
1 |
[[7,26,6,60],[1,29,15,52],[11,56,8,20],[11,31,8,47],[7,52,6,33],[11,55,9,22],[3,71,17,6],[1,31,22,44],[2,54,18,22],[21,47,4,26],[1,40,23,34],[11,66,9,12],[10,68,8,12]] |
2 |
=pca(A1) |
3 |
=A2(2).((~)/sum(A2(2))) |
4 |
=A3.(cum(~)) |
5 |
=pca@r(A1,2) |
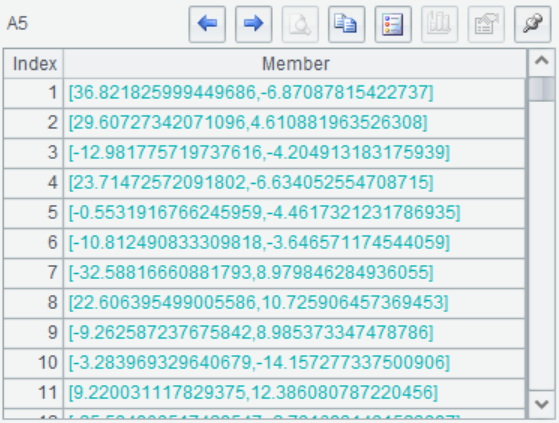
A1 矩阵的行对应样本,列对应变量
A2 对A1进行主成分分析,返回降维用的信息
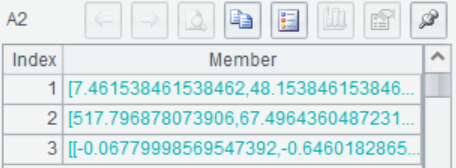
A2(1) 返回每一列的平均值
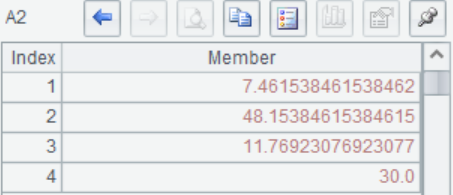
A2(2) 主成分方差,也就是各特征向量对应的特征值,从大到小进行排列
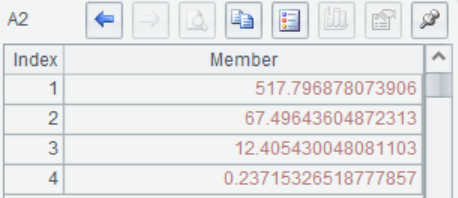
A1(3) 主成分系数,也就是样本协方差矩阵的特征向量矩阵
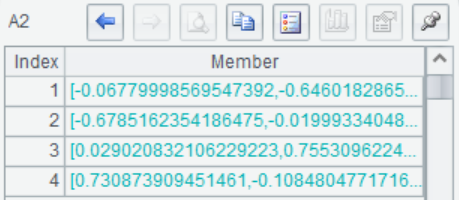
A3 计算四个特征值的信息贡献率
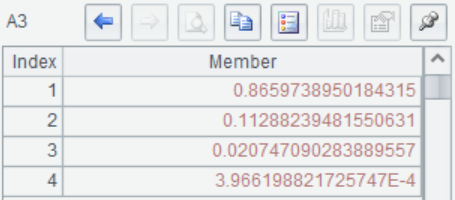
A4 计算累计贡献率,可以看到前两个特征之和已经达到97% 以上,因此可以取前两个主成分。
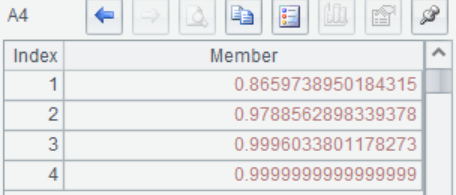
A5 对A1进行降维,n 值取 2,返回降维结果。