回归模型的假设检验
在多元线性回归模型中，因变量y 和自变量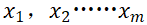
之间是否存在线性关系以及回归系数的显著性是需要检验的，比如在下面的例子中我们可以通过F 检验和 t 检验来分析判断自变量和因变量之间的关系。
表中的数据为某养猪场25 头育肥猪 4 个胴体性状的数据资料，需要进行瘦肉量 y 对眼肌面积x1、腿肉量x2、腰肉量x3的多元回归分析
序号 |
眼肌面积x1 |
腿肉量x2 |
腰肉量x3 |
瘦肉量y |
1 |
23.73 |
5.49 |
1.21 |
15.02 |
2 |
22.34 |
4.32 |
1.35 |
12.62 |
3 |
28.84 |
5.04 |
1.92 |
14.86 |
4 |
27.67 |
4.72 |
1.49 |
13.98 |
5 |
20.83 |
5.35 |
1.56 |
15.91 |
6 |
22.27 |
4.27 |
1.5 |
12.47 |
7 |
27.57 |
5.25 |
1.85 |
15.8 |
8 |
28.01 |
4.62 |
1.51 |
14.32 |
9 |
24.79 |
4.42 |
1.46 |
13.76 |
10 |
28.96 |
5.3 |
1.66 |
15.18 |
11 |
25.77 |
4.87 |
1.64 |
14.2 |
12 |
23.17 |
5.8 |
1.9 |
17.07 |
13 |
28.57 |
5.22 |
1.66 |
15.4 |
14 |
23.52 |
5.18 |
1.98 |
15.94 |
15 |
21.86 |
4.86 |
1.59 |
14.33 |
16 |
28.95 |
5.18 |
1.37 |
15.11 |
17 |
24.53 |
4.88 |
1.39 |
13.81 |
18 |
27.65 |
5.02 |
1.66 |
15.58 |
19 |
27.29 |
5.55 |
1.7 |
15.85 |
20 |
29.07 |
5.26 |
1.82 |
15.28 |
21 |
32.47 |
5.18 |
1.75 |
16.4 |
22 |
29.65 |
5.08 |
1.7 |
15.02 |
23 |
22.11 |
4.9 |
1.81 |
15.73 |
24 |
22.43 |
4.65 |
1.82 |
14.75 |
25 |
20.04 |
5.08 |
1.53 |
14.35 |
要求：（1）求 y 关于x1，x2，x3的线性回归方程
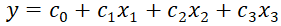
计算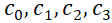
的估计值
(2)对上述回归模型和回归系数进行检验，显著性水平α取0.05
分析：
（1）线性回归可以采用最小二乘法进行拟合，使用linefit()，返回拟合回归系数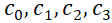
（2）使用F 检验 y 和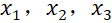
之间是否存在线性关系，如通过检验，则继续使用t 检验回归系数的显著性，需要计算的统计量有：F，
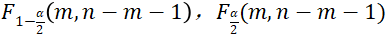，t，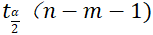
。
计算公式如下：
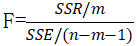
其中：m 表示分子自由度，n 表示样本数量
回归平方和：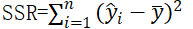
残差平方和：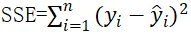
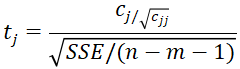
其中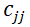
为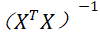
中的第（j+1,j+1）个元素
，
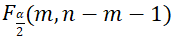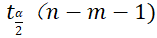可使用逆累积函数finv()和tinv()计算
用SPL 实现计算：
（1）采用最小二乘法，拟合回归方程
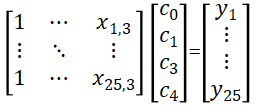
求解出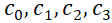的估计值
A |
B |
C |
D |
|
1 |
[[1,23.73,5.49,1.21],[1,22.34,4.32,1.35],[1,28.84,5.04,1.92],[1,27.67,4.72,1.49], [1,20.83,5.35,1.56],[1,22.27,4.27,1.5],[1,27.57,5.25,1.85],[1,28.01,4.62,1.51], [1,24.79,4.42,1.46],[1,28.96,5.3,1.66],[1,25.77,4.87,1.64],[1,23.17,5.8,1.9], [1,28.57,5.22,1.66],[1,23.52,5.18,1.98],[1,21.86,4.86,1.59],[1,28.95,5.18,1.37], [1,24.53,4.88,1.39],[1,27.65,5.02,1.66],[1,27.29,5.55,1.7],[1,29.07,5.26,1.82], [1,32.47,5.18,1.75],[1,29.65,5.08,1.7],[1,22.11,4.9,1.81],[1,22.43,4.65,1.82], [1,20.04,5.08,1.53]] |
3 |
25 |
0.05 |
2 |
[15.02,12.62,14.86,13.98,15.91,12.47,15.8,14.32,13.76,15.18,14.2,17.07, 15.4,15.94,14.33,15.11,13.81,15.58,15.85,15.28,16.4,15.02,15.73,14.75,14.35] |
|||
3 |
=linefit(A1,A2) |
A1 输入矩阵X
B1 输入m 值，本例中 m=3
C1输入n 值，本例中 n=25
D1输入α，本例中α=0.25
A2 输入Y
A3 最小二乘拟合方程组，返回回归系数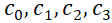的估计值
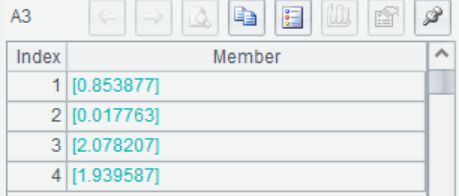
（2）使用F 检验因变量 y 与自变量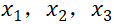
之间是否存在线性关系。令原假设为
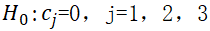。在显著性水平α下，若
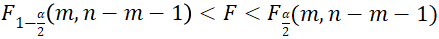，则接受
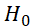，否则拒绝
A |
B |
C |
D |
|
… |
… |
|||
4 |
=mul(A1,A3).conj() |
|||
5 |
=(A2--A4).sum(~*~) |
|||
6 |
=A2.avg() |
|||
7 |
=A4.sum((~-A6)*(~-A6)) |
|||
8 |
=(A7/B1)/(A5/(C1-B1-1)) |
|||
9 |
=finv((D1/2),B1,(C1-B1-1)) |
|||
10 |
=finv((1-D1/2),B1,(C1-B1-1)) |
|||
11 |
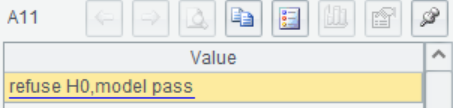
=if(A8>A9&&A8<A10,"accept H0,model do not pass","refuse H0,model pass") |
A4 将X 与回归系数相乘，得到预测值
A5 计算残差平方和SSE
A6 计算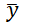
A7 计算回归平方和SSR
A8 计算统计量F，F=37.753
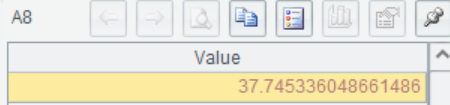
A9使用F 逆累积分布函数 finv()计算上1-α/2分位数
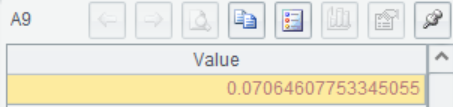
A10 使用F 逆累积分布函数 finv()计算上α/2分位数
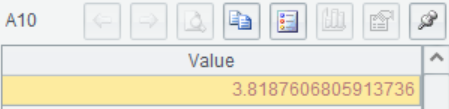
A11 比较F和
，
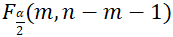，返回检验结果
（3）当H0被拒绝时,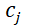
不全为0，但不排除其中若干个等于 0，所以应进一步做 m+1个t 检验：
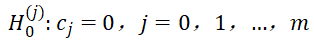
对于给定的α，若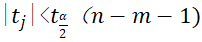
，则接受，否则拒绝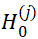
A |
B |
C |
D |
|
… |
… |
|||
=inverse(mul(transpose(A1),A1)) |
||||
13 |
=A3.conj().(~/sqrt(A12(#)(#))/sqrt(A5/(C1-B1-1))) |
|||
14 |
=tinv((1-D1/2),(C1-B1-1)) |
|||
15 |
=A13.(if(abs(~)<A14,"accept c"/(#-1)/"=0","refuse c"/(#-1)/"=0")) |
A12 计算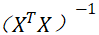
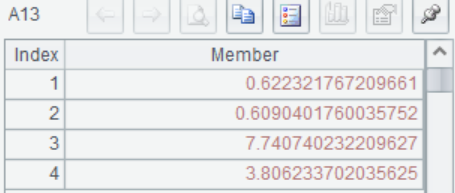
A13 计算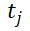
，从上到下依次为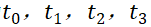
A14 使用t逆累积分布函数tinv()计算t 分布的上α/2分位数
A15比较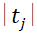
和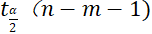
，返回检验结果
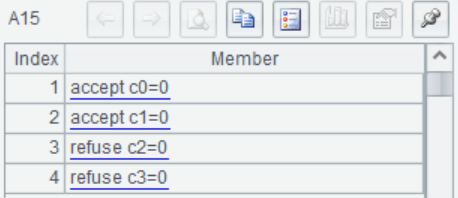
由结果可知变量x1对模型的影响是不显著的，建立线性模型时可以不使用x1
