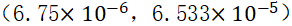参数估计
在参数估计和假设检验中，常常需要构造分布函数，在SPL 中提供了常见分布的逆累积分布函数（ICDF）。SPL 中的逆累积分布函数有：norminv()，tinv()，chi2inv()，finv()，分别表示正态分布，T 分布，卡方分布，F 分布。
例如，有一批产品寿命的变量服从正态分布，均值mu=4，标准差sigma=1.3，单位是年，计算 10%的产品失效所需时间
A |
|
1 |
=norminv(0.1,4,1.3) |
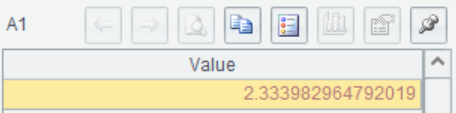
A1采用正态逆累积分布函数，带入概率值、均值和标准差，返回2.334，即 10% 得产品失效所需时间为 2.334 年
使用逆累积分布函数还可以进行区间估计
例如，使用金球测定引力常数（单位：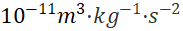
），测定观察值为
6.683，6.681，6.676，6.678，6.679，6.672
设测定值总体为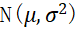
，
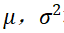均未知，求
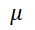的置信度为0.9 的置信区间，并求
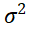的置信度为0.9 的置信区间。
当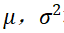均未知时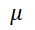，的置信区间公式为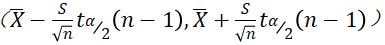
其中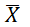
为样本均值，S 为样本标准差，n为样本容量
在本例中1-α=0.9，n=6，带入公式
用SPL 代码计算
的区间估计
A |
B |
C |
|
1 |
[6.683,6.681,6.676,6.678,6.679,6.672] |
0.9 |
6 |
2 |
=tinv(1-(1-B1)/2,C1-1) |
||
3 |
=sqrt(var@s(A1))/sqrt(C1)*A2 |
||
4 |
=avg(A1) |
||
5 |
=[A4-A3,A4+A3] |
A1 输入样本数据
B1 置信度，即1-α
C1 样本容量n
A2 使用T 分布逆累积函数tinv(p, nu)计算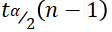
，p 表示累积概率，nu 表示自由度，即 p=1-α/2=0.95，nu=n-1=5
A3 计算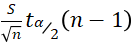
A4 计算样本均值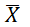
A5 带入A3和A4的结果，计算置信区间，根据返回值得到总体均值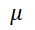，在置信度为0.9 时的置信区间为（6.675，6.681）
同理，方差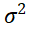的置信区间公式为
，
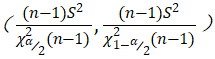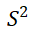为样本方差
SPL计算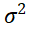的区间估计
A |
B |
C |
|
1 |
[6.683,6.681,6.676,6.678,6.679,6.672] |
0.9 |
6 |
2 |
=var@s(A1) |
||
3 |
=chi2inv(1-(1-B1)/2,C1-1) |
||
4 |
=chi2inv((1-B1)/2,C1-1) |
||
5 |
=[(C1-1)*A2/A3,(C1-1)*A2/A4] |
A1 输入样本数据
B1 置信度，即1-α
C1 样本容量n
A2计算样本方差
A3使用卡方分布逆累积函数chi2inv(p, v)计算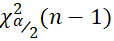
，p 表示累积概率，v表示自由度，即p=1-α/2=0.95，nu=n-1=5
A4计算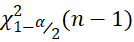
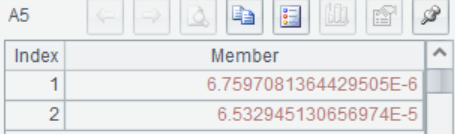
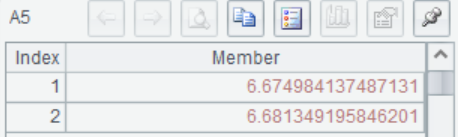
A5计算置信区间，根据返回值得到总体方差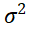，在置信度为0.9 时的置信区间为
